neste: 3.4 kjøleskap og varme opp: 3. Den Første Loven Forrige: 3.2 Generalisert Representasjon Av Innhold Index
En Carnot syklus er vist I Figur 3.4. Det harfire prosesser. Det er to adiabatiske reversible ben og toisothermal reversible ben. Vi kan konstruere En Carnot-syklus medmange forskjellige systemer, men konseptene kan vises ved hjelp av en kjent arbeidsfluid, den ideelle gassen. Systemet kan betraktes somet kammer omsluttet av et stempel og fylt med denne ideelle gassen.
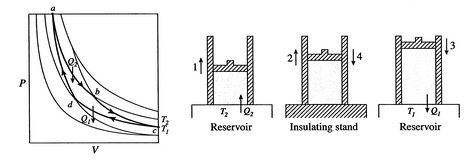
de fire prosessene I Carnot syklusen er:
- systemet er ved temperatur
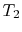 ved tilstand
ved tilstand  . Det er brakt i kontakt med et varmereservoar, som bare er en væske ellersolid masse av stor nok grad slik at temperaturen ikke endres merkbart når en viss mengde varme overføres tilsystem. Med andre ord er varmereservoaret en konstant temperaturkilde (eller mottaker) av varme. Systemet gjennomgår deretter anisotermisk utvidelse fra
. Det er brakt i kontakt med et varmereservoar, som bare er en væske ellersolid masse av stor nok grad slik at temperaturen ikke endres merkbart når en viss mengde varme overføres tilsystem. Med andre ord er varmereservoaret en konstant temperaturkilde (eller mottaker) av varme. Systemet gjennomgår deretter anisotermisk utvidelse fra  til
til  , med varme absorbert
, med varme absorbert 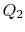 .
. - Atstate
 , systemet er termisk isolert (fjernet fra kontaktmed varmereservoaret) og la deretter utvide til
, systemet er termisk isolert (fjernet fra kontaktmed varmereservoaret) og la deretter utvide til  . Under thisexpansion temperaturen synker til
. Under thisexpansion temperaturen synker til  . Varmevekslet under denne delen av syklusen,
. Varmevekslet under denne delen av syklusen, 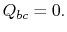 )
) - ved tilstand
 systemet er brakt i kontakt med et varmebeholder ved temperatur
systemet er brakt i kontakt med et varmebeholder ved temperatur  . Det er deretter komprimert til stat
. Det er deretter komprimert til stat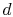 , avviser varme
, avviser varme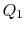 i prosessen.
i prosessen. - endelig komprimeres systemet adiabatisk tilbake til den første tilstanden
 . Varmevekslingen
. Varmevekslingen 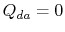 .
.
den termiske effektiviteten til syklusen er gitt ved definisjonen
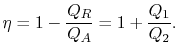 |
(3..4) |
i denne ligningen er det en tegnkonvensjon underforstått. Mengdene![]()
![]() som definert er størrelsene til varmen absorbert ogjected. Mengdene
som definert er størrelsene til varmen absorbert ogjected. Mengdene ![]()
![]() på den annen side er definedwith referanse til varme mottatt av systemet. I dette eksemplet er dentidligere negativ og sistnevnte er positiv. Varmen absorbert ogjektert av systemet finner sted under isotermiske prosesser ogvi vet allerede hva deres verdier er Fra Eq.(3.1):
på den annen side er definedwith referanse til varme mottatt av systemet. I dette eksemplet er dentidligere negativ og sistnevnte er positiv. Varmen absorbert ogjektert av systemet finner sted under isotermiske prosesser ogvi vet allerede hva deres verdier er Fra Eq.(3.1):
Theefficiency kan nå skrives i form av volumene ved forskjellige tilstander som
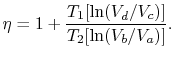 |
(3..5) |
The path from states ![]() to
to ![]() and from
and from ![]() to
to ![]() are bothadiabatic and reversible. For a reversible adiabatic process we knowthat
are bothadiabatic and reversible. For a reversible adiabatic process we knowthat ![]() . Using the ideal gas equation ofstate, we have
. Using the ideal gas equation ofstate, we have ![]() . Along curve
. Along curve![]()
![]() , therefore,
, therefore, ![]() . Alongthe curve
. Alongthe curve ![]()
![]()
![]() . Thus,
. Thus,

Comparing the expression for thermal efficiencyEq. (3.4) with Eq. (3.5) showsto konsekvenser. For det første relateres de mottatte og avviste heatene til temperaturene i de isotermiske delene av syklusen med
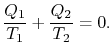 |
(3..6) |
For Det Andre blir Effektiviteten til En Carnot – syklus gitt kompakt av
 |
(3..7) |
effektiviteten kan bare være 100% hvis temperaturen dervarme avvises er null. Varme-og arbeidsoverføringene til og frasystemet vises skjematisk i figur 3.5.
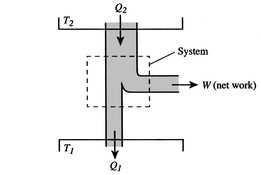
Gjørmete Poeng
Siden ![]() , ser På
, ser På ![]()
![]() grafen, betyr det at jo lenger fra hverandre
grafen, betyr det at jo lenger fra hverandre ![]()
![]() isotermer er, denstørre effektivitet? Og at hvis de var veldig nært, ville det væreveldig ineffektiv? (MP 3.2)
isotermer er, denstørre effektivitet? Og at hvis de var veldig nært, ville det væreveldig ineffektiv? (MP 3.2)
I Carnot syklusen, hvorfor handler vi bare om volumendringer ogikke trykkendringer på adiabatene og isotermene?(MP 3.3)
er det en fysisk søknad om Carnot-syklusen? Kan Vi designe En Carnot-motor for en fremdriftsenhet?(MP 3.4)
Hvordan vet vi hvilke sykluser som skal brukes som modeller for virkelige prosesser?(MP 3.5)
neste: 3.4 kjøleskap og varme opp: 3. Den Første Loven Forrige: 3.2 Generalisert Representasjon Av Innhold Index
UnifiedTP