Forstå Logistisk Regresjon I Python

Klassifiseringsteknikker er en viktig del av maskinlæring og data mining applikasjoner. Omtrent 70% av problemene I Datavitenskap er klassifiseringsproblemer. Det er mange klassifiseringsproblemer som er tilgjengelige, men logistikkregresjonen er vanlig og er en nyttig regresjonsmetode for å løse det binære klassifiseringsproblemet. En annen kategori av klassifisering Er Multinomial klassifisering, som håndterer problemene der flere klasser er til stede i målvariabelen. FOR EKSEMPEL, IRIS datasett et meget kjent eksempel på multi-klasse klassifisering. Andre eksempler er klassifisering av artikkel / blogg / dokumentkategori.

Logistisk Regresjon kan brukes for ulike klassifiseringsproblemer som spam deteksjon. Diabetes prediksjon, hvis en gitt kunde vil kjøpe et bestemt produkt eller vil de churn en annen konkurrent, om brukeren vil klikke på en gitt annonse link eller ikke, og mange flere eksempler er i bøtte.Logistisk Regresjon Er en av de mest enkle Og brukte Maskinlæringsalgoritmer for to-klasse klassifisering. Det er enkelt å implementere og kan brukes som grunnlinje for ethvert binært klassifiseringsproblem. Dens grunnleggende grunnleggende begreper er også konstruktive i dyp læring. Logistisk regresjon beskriver og estimerer forholdet mellom en avhengig binær variabel og uavhengige variabler.

I Denne opplæringen vil du lære Følgende ting I Logistisk Regresjon:

• Introduksjon til Logistisk Regresjon
• Lineær Regresjon Vs. Logistisk Regresjon
• Maksimal Sannsynlighet Estimering Vs. Ordinær Minste Kvadratmetode
• hvordan Fungerer Logistisk Regresjon?
• Modellbygging I Scikit-lær
• Modellevaluering ved Hjelp Av Forvirringsmatrise.Fordeler Og Ulemper Ved Logistisk Regresjon

Logistisk Regresjon

Logistisk regresjon Er en statistisk metode for å forutsi binære klasser. Utfallet eller målvariabelen er dikotom i naturen. Dikotom betyr at det bare er to mulige klasser. For eksempel kan den brukes til kreftdeteksjonsproblemer. Det beregner sannsynligheten for en hendelse forekomst.

det er et spesielt tilfelle av lineær regresjon der målvariabelen er kategorisk i naturen. Den bruker en logg av odds som den avhengige variabelen. Logistic Regression predicts the probability of occurrence of a binary event utilizing a logit function.

Linear Regression Equation:

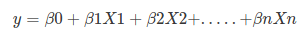
Where, y is dependent variable and x1, x2 … and Xn are explanatory variables.

Sigmoid Function:

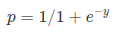
Apply Sigmoid function on linear regression:

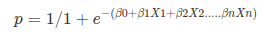
Properties of Logistic Regression:

• den avhengige variabelen i logistisk regresjon følger Bernoulli-Distribusjonen.
• Estimering gjøres gjennom maksimal sannsynlighet.
• Ingen R Kvadrat, modell fitness beregnes Gjennom Konkordans, KS-Statistikk.

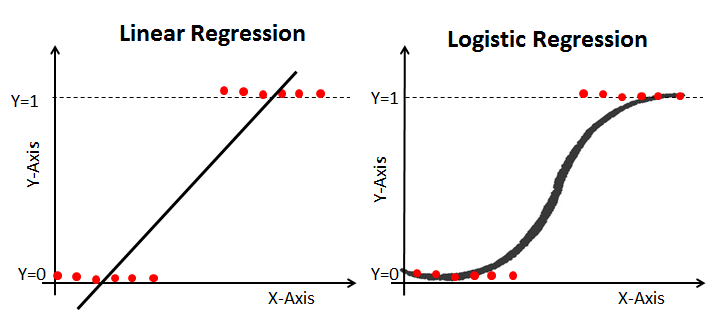
Lineær Regresjon Vs. Logistisk Regresjon

Lineær regresjon gir deg en kontinuerlig utgang, men logistisk regresjon gir en konstant utgang. Et eksempel på kontinuerlig produksjon er boligpris og aksjekurs. Eksempel på diskret utgang er å forutsi om en pasient har kreft eller ikke, forutsi om kunden vil churn. Lineær regresjon estimeres Ved Hjelp Av Vanlige Minste Kvadraters (OLS) mens logistisk regresjon estimeres Ved Hjelp Av Maksimal Sannsynlighet Estimering (Mle) tilnærming.

Maksimal Sannsynlighet Estimering Vs. Minste Kvadratmetode

MLE er en «sannsynlighet» maksimeringsmetode, MENS OLS er en avstandsminimerende tilnærmingsmetode. Maksimering av sannsynlighetsfunksjonen bestemmer parametrene som mest sannsynlig vil produsere de observerte dataene. Fra et statistisk synspunkt setter mle gjennomsnitt og varians som parametere ved å bestemme de spesifikke parametriske verdiene for en gitt modell. Dette settet med parametere kan brukes til å forutsi dataene som trengs i en normalfordeling.

Vanlige Minste kvadraters estimater beregnes ved å montere en regresjonslinje på gitte datapunkter som har minimumssummen av de kvadrerte avvikene (minste kvadratfeil). Begge brukes til å estimere parametrene til en lineær regresjonsmodell. MLE antar en felles sannsynlighetsmassefunksjon, MENS OLS ikke krever noen stokastiske forutsetninger for å minimere avstand.

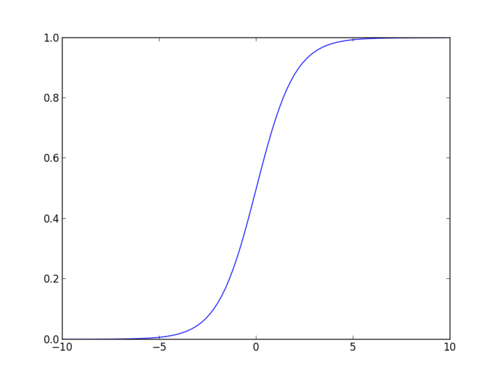
Sigmoid-Funksjonen

sigmoid-funksjonen, også kalt logistisk funksjon, gir en S-formet kurve som kan ta et hvilket som helst virkelig verdsatt tall og kartlegge det til en verdi mellom 0 og 1. Hvis kurven går til positiv uendelig, vil y spådd bli 1, og hvis kurven går til negativ uendelig, vil y spådd bli 0. Hvis utgangen av sigmoid-funksjonen er mer enn 0,5, kan vi klassifisere utfallet som 1 ELLER JA, og hvis det er mindre enn 0.5, vi kan klassifisere det som 0 eller NEI. For eksempel: hvis utgangen er 0,75, kan vi si i form av sannsynlighet som: det er en 75 prosent sjanse for at pasienten vil lide av kreft.

typer logistisk regresjon

typer logistisk regresjon:

• binær logistisk regresjon: målvariabelen har bare to mulige utfall som spam eller ikke spam, kreft eller ingen kreft.Multinomial Logistisk Regresjon: målvariabelen har tre eller flere nominelle kategorier som å forutsi Typen Vin.
• Ordinær Logistisk Regresjon: målvariabelen har tre eller flere ordinære kategorier som restaurant eller produktklassifisering fra 1 til 5.

Modellbygging I Scikit-lær

La oss bygge diabetes prediksjon modell.

Her skal du forutsi diabetes ved Hjelp Av Logistisk Regresjonsklassifisering.

La oss først laste inn det nødvendige Pima Indian Diabetes datasettet ved hjelp av pandas ‘ les CSV-funksjon. Du kan laste ned data fra følgende lenke: https://www.kaggle.com/uciml/pima-indians-diabetes-database

Laster Data

#import pandasimport pandas as pdcol_names = # load datasetpima = pd.read_csv("pima-indians-diabetes.csv", header=None, names=col_names)

pima.head()

velge funksjon

her må du dele de oppgitte kolonnene i to typer variabler avhengig(eller målvariabel) og uavhengig variabel(eller funksjonsvariabler).

#split dataset in features and target variablefeature_cols = X = pima # Featuresy = pima.label # Target variable

Splitting Data

for å forstå modellens ytelse, er det en god strategi å dele datasettet i et treningssett og et testsett.

la oss dele datasett ved hjelp av funksjonen train_test_split(). Du må passere 3 parametere funksjoner, mål og test_set størrelse. I tillegg kan du bruke random_state til å velge poster tilfeldig.

# split X and y into training and testing setsfrom sklearn.cross_validation import train_test_splitX_train,X_test,y_train,y_test=train_test_split(X,y,test_size=0.25,random_state=0)

/home/admin/.local/lib/python3.5/site-packages/sklearn/cross_validation.py:41: DeprecationWarning: This module was deprecated in version 0.18 in favor of the model_selection module into which all the refactored classes and functions are moved. Also, note that the interface of the new CV iterators is different from that of this module. This module will be removed in 0.20. "This module will be removed in 0.20.", DeprecationWarning)

Her er Datasettet brutt i to deler i et forhold på 75:25. Det betyr at 75% data vil bli brukt til modellopplæring og 25% for modelltesting.

Modellutvikling og Prediksjon

importer Først Den Logistiske Regresjonsmodulen og opprett Et Logistisk Regresjonsklassifiseringsobjekt ved Hjelp Av LogisticRegression () – funksjonen.

monter deretter modellen på togsettet ved hjelp av fit () og utfør prediksjon på testsettet ved hjelp av predict ().

# import the classfrom sklearn.linear_model import LogisticRegression# instantiate the model (using the default parameters)logreg = LogisticRegression()# fit the model with datalogreg.fit(X_train,y_train)#y_pred=logreg.predict(X_test)

Modellevaluering ved Hjelp Av Forvirringsmatrise

en forvirringsmatrise er en tabell som brukes til å evaluere ytelsen til en klassifiseringsmodell. Du kan også visualisere ytelsen til en algoritme. Det grunnleggende i en forvirringsmatrise er antall korrekte og feilaktige spådommer oppsummeres klassevis.

# import the metrics classfrom sklearn import metricscnf_matrix = metrics.confusion_matrix(y_test, y_pred)cnf_matrix

array(, ])

her kan du se forvirringsmatrisen i form av arrayobjektet. Dimensjonen til denne matrisen er 2 * 2 fordi denne modellen er binær klassifisering. Du har to klasser 0 og 1. Diagonale verdier representerer nøyaktige spådommer, mens ikke-diagonale elementer er unøyaktige spådommer. I utdataene er 119 og 36 faktiske spådommer, og 26 og 11 er feil spådommer.

Visualisere Forvirringsmatrise ved Hjelp Av Heatmap

la oss visualisere resultatene av modellen i form av en forvirringsmatrise ved hjelp av matplotlib og seaborn.

Her vil du visualisere forvirringsmatrisen ved Hjelp Av Heatmap.

# import required modulesimport numpy as npimport matplotlib.pyplot as pltimport seaborn as sns%matplotlib inline

class_names= # name of classesfig, ax = plt.subplots()tick_marks = np.arange(len(class_names))plt.xticks(tick_marks, class_names)plt.yticks(tick_marks, class_names)# create heatmapsns.heatmap(pd.DataFrame(cnf_matrix), annot=True, cmap="YlGnBu" ,fmt='g')ax.xaxis.set_label_position("top")plt.tight_layout()plt.title('Confusion matrix', y=1.1)plt.ylabel('Actual label')plt.xlabel('Predicted label')

Text(0.5,257.44,'Predicted label')

forvirring matrise evaluering beregninger

la oss evaluere modellen ved hjelp av modell evaluering beregninger som nøyaktighet, presisjon og tilbakekalling.

print("Accuracy:",metrics.accuracy_score(y_test, y_pred))print("Precision:",metrics.precision_score(y_test, y_pred))print("Recall:",metrics.recall_score(y_test, y_pred))

Accuracy: 0.8072916666666666Precision: 0.7659574468085106Recall: 0.5806451612903226

vel, du har en klassifiseringsrate på 80%, betraktet som god nøyaktighet.Presisjon: Presisjon handler om å være presis, dvs. hvor nøyaktig modellen din er. Med andre ord kan du si når en modell gjør en prediksjon, hvor ofte er det riktig. I din prediksjon tilfelle, når Logistisk Regresjonsmodell spådd pasienter kommer til å lide av diabetes, at pasienter har 76% av tiden.

Recall: Hvis det er pasienter som har diabetes i testsettet, og Din Logistiske Regresjonsmodell kan identifisere den 58% av tiden.

ROC Kurve

Mottaker Driftskarakteristikk (ROC) kurve er et plott av den sanne positive frekvensen mot den falske positive frekvensen. Det viser forskjellen mellom sensitivitet og spesifisitet.

y_pred_proba = logreg.predict_proba(X_test)fpr, tpr, _ = metrics.roc_curve(y_test, y_pred_proba)auc = metrics.roc_auc_score(y_test, y_pred_proba)plt.plot(fpr,tpr,label="data 1, auc="+str(auc))plt.legend(loc=4)plt.show()

AUC-poengsum for saken er 0,86. AUC score 1 representerer perfekt klassifikator, og 0,5 representerer en verdiløs klassifikator.

Fordeler

På grunn av sin effektive og enkle natur, krever ikke høy beregningskraft, enkel å implementere, lett tolkbar, brukt mye av dataanalytiker og forsker. Også, det krever ikke skalering av funksjoner. Logistisk regresjon gir en sannsynlighetsscore for observasjoner.

Ulemper

Logistisk regresjon er ikke i stand til å håndtere et stort antall kategoriske funksjoner / variabler. Det er sårbart for overfitting. Også, kan ikke løse det ikke-lineære problemet med logistisk regresjon, derfor krever det en transformasjon av ikke-lineære funksjoner. Logistisk regresjon vil ikke fungere bra med uavhengige variabler som ikke er korrelert med målvariabelen og er svært like eller korrelert med hverandre.

Konklusjon

i denne opplæringen dekket du mange detaljer om Logistisk Regresjon. Du har lært hva logistisk regresjon er, hvordan du bygger respektive modeller, hvordan du visualiserer resultater og noe av den teoretiske bakgrunnsinformasjonen. Du dekket også noen grunnleggende begreper som sigmoid-funksjonen, maksimal sannsynlighet, forvirringsmatrise, ROC-kurve.

Forhåpentligvis kan du nå bruke Logistisk Regresjonsteknikk for å analysere dine egne datasett. Takk for at du leser denne opplæringen!

hvis Du vil lære mer Om Logistisk Regresjon, ta Datacamps Grunnlag for Prediktiv Analyse I Python (Del 1) kurs.