Kompetanse: Intermediate
Hva er en spline funksjon ? vi trenger å vite hva de essensielle egenskapene til splines er før vi vurderer hvordan vi skal konstruere et basissystem for dem.
Spline funksjoner dannes ved å bli polynomer sammen på faste punktkalt knop. Det vil si at vi deler intervallet som strekker seg fra nedre grense tL toupper grense tU over hvilken vi ønsker å tilnærme en kurve til L + 1 sub-intervalsseparert Med l indre grenser ξ kalt knop, eller noen ganger brytepunkter.)Det er et skille mellom disse to begrepene, men vi vil komme til dette senere.
Vurdere det enkleste tilfellet der en enkelt stoppunkt deler intervall i to delintervaller. Splinefunksjonen er innenfor hvert intervall et polynom av spesifisert grad (den høyeste kraften som definerer polynomet) eller rekkefølge (antall koeffisienter som definerer polynomet, som er en merenn sin grad). La oss bruke m til å betegne rekkefølgen av polynomet, slik atgraden er m-1:
ved det indre brytepunktet ξ 1, må de to polynomene bli med jevnt. I det vanligste tilfellet betyr dette at derivatene samsvarer med ordren en mindre enn graden. Faktisk, hvis de matchet opp til derivatet hvis rekkefølge likte graden, ville de være det samme polynomet. Dermed har en spline-funksjon definert i dette var en ekstra grad av frihet enn et polynom som strekker seg over hele intervallet.
la for eksempel hvert polynom være et rettlinjesegment, og derfor av grad en. I dette blir de med i brytepunktet med matchende derivateropp til grad 0; kort sagt, de blir bare med og har identiske verdier ved bruddpunktet. Siden det første polynomet har to frihetsgrader (skråning og avskjæring), og den andre, som allerede har sin verdi definert ved bruddpunktet, er igjen med bare en grad av frihet( skråning), har den totale polygonale linjen trefrihetsgrader.
Tilsvarende, hvis begge polynomene er quadratics, så samsvarer både i form av verdier og i form ofslope av første derivativved ξ 1. Det første polynomet har tre frihetsgrader, men det andre taper to fordi hvisbegrensningen på verdien og skråningen ved ξ, og beholder dermed bareen. Dette etterlater totalt fire frihetsgrader for splinefunksjonendannet på denne måten, sommotsatt til tre for et kvadratisk polynom over hele intervallet. Figur 1 viser disselineære og kvadratiske tilfeller med et enkelt stoppunkt.
hva er noen eksempler på vanlige basisfunksjoner?
Vi kan nå generalisere situasjonen Til l indre brytepunkter, anda spline – funksjonen er av orden m eller grad m-1 over eachsub-intervall. Det første polynomsegmentet har et fullt komplementav m frihetsgrader, men hvert etterfølgende segment har bare engrad avfrihet på grunn av m-1-begrensningene på dens oppførsel.Dette gir totalt L + m frihetsgrader, eller antallinterior breakpoints pluss rekkefølgen av polynomsegmentene.dermed er spline-funksjoner i hovedsak generaliseringer av begrepet polygonallines. De får sin fleksibilitet på to måter: Først, etter rekkefølgen avpolynomier som de er bygget fra, og for det andre, etter antall bruddpunkterbrukt. Vi velger vanligvis å holde ordren fast, og legger til avbruddspunkter for å få den nødvendige fleksibiliteten.
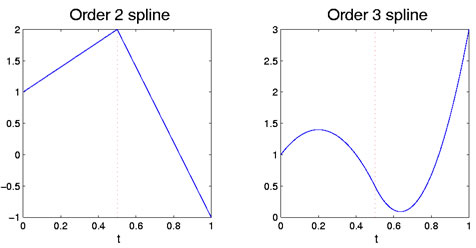
Figur 1: den venstre figuren viser en ordre to spline-funksjon, som er stykkevis lineær. Den riktige figuren er en ordre 3 spline, somer stykkevis kvadratisk. Brekkpunktet på 0,5 er angitt med den røde vertikale stiplede linjen.