Maksimal Parsimoni på Fylogenetiske nettverk

Definisjon av fylogenetiske nettverk

vi følger definisjonen av fylogenetiske nettverk som gitt i , Definisjon 4, side 16]. For alle andre grafteoretiske definisjoner som ikke er gitt her, følger vi . Et rotfestet fylogenetisk nettverk, ganske enkelt kalt her et fylogenetisk nettverk, er definert som en rotfestet, rettet acyklisk graf (DAG), hvis rot har indegree 0 og bladene har outegree 0. Hjørnene hvis indegree er større enn 1 kalles retikulerte hjørner, og kantene med retikulerte hjørner som hodevern kalles retikulerte kanter. Alle andre kanter kalles trekanter. Definisjonen gitt i tar seg av den såkalte «time-consistency» restraint, nemlig at trekantene finner sted i en positiv tid og de retikulære toppene har foreldre som bare kan «sameksistere i tide». Derfor, fremover, husker vi den formelle definisjonen av fylogenetiske nettverk som gitt i .Gitt en hvilken som helst rettet graf, sier vi at to hjørner u og v ikke kan sameksistere i tid hvis det finnes en sekvens P = (p1, p2,…, p k ) av stier I n slik at:

1. p i er en rettet sti som inneholder minst en trekant, for hver 1 ≤ i ≤ k,

2. u er halen til p 1, og v er hodet til p k , og

3. for hver 1 ≤ i ≤ k – 1, finnes det et nettverk toppunkt hvis to foreldre er hodet til p i og halen til p i+1.

et fylogenetisk nettverk N er en rotfestet DAG som adlyder følgende begrensninger:

1. Hvert toppunkt har indegree og outegree definert av en av de fire kombinasjonene (0, 2), (1, 0), (1, 2), eller (2, 1) – tilsvarende henholdsvis rot, blader, indre tre hjørner og retikulere hjørner. Alle andre hjørner enn retikulerte hjørner kalles tre hjørner.

2. hvis to hjørner u og v ikke kan sameksistere i tid, eksisterer det ikke et nettverk vertex w med kanter (u, w) og (v, w).

3. Gitt en kant av nettverket, må minst ett av endepunktene være et tre-toppunkt.En annen komponent i denne definisjonen er at for enhver kant i det fylogenetiske nettverket er minst ett av dets endepunkter (enten hodet eller halen) et tre-toppunkt. Her vil vi bruke denne definisjonen. Når det er mulig, peker vi på om betingelsene i definisjonen er nødvendige.Fylogenetiske nettverk kan naï betraktes som et nettverk som inneholder som undergrafer, trærne som forklarer de evolusjonære historiene til forskjellige segmenter av inngangsterminalsekvensene. Gitt et fylogenetisk nettverk garanterer ikke sletting av en av hver kanthendelse til et retikulert toppunkt et resulterende fylogenetisk tre med samme sett med blader som nettverket. Dette er en uønsket egenskap, spesielt hvis parsimony kriteriet er definert ved å finne et fylogenetisk tre inne i nettverket som er mest parsimonious for det gitte området, som definert i . For å unngå dette problemet er det nødvendig å anta at ingen indre toppunkt har to retikulerte barn. Vi kaller denne klassen av fylogenetiske nettverk som et fylogenetisk nettverk uten søsterretikulasjoner. Se Figur 1 for noen eksempler på fylogenetiske nettverk.

   

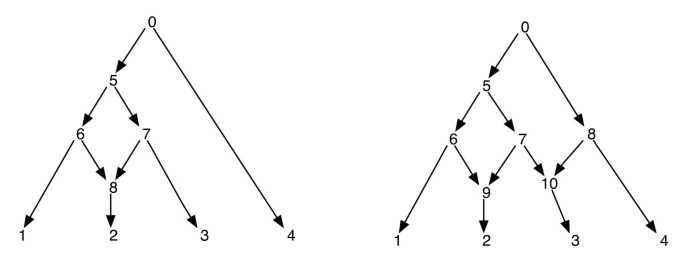
   Fylogenetiske Nettverk. Figuren viser to fylogenetiske nettverk; den til venstre har bare et enkelt retikulært toppunkt og den til høyre har to retikulære toppunkter som er søstre til hverandre. Merk at fjerning av kantene (7, 9) og (7, 10) fra nettverket til høyre ikke resulterer i et tre der vertex 7 er et blad. Dette viser at fjerning av en innkommende kant hver per retikulert vertex ikke nødvendigvis produserer et tre med samme bladsett som nettverket. Post-bestilling og forhåndsbestilling av hjørner av nettverket til venstre er 1, 2, 8, 6, 3, 7, 5, 4, 0 og 0, 5, 6, 1, 8, 2, 7, 3, 4 henholdsvis og for nettverket til høyre er de 1, 2, 9, 6, 3, 10, 7, 5, 4, 8, 0 og 0, 5, 6, 1, 9, 2, 7, 10, 3, 8, 4 henholdsvis.

   Før vi går videre til definisjonen av parsimonyproblemer, er følgende en nyttig observasjon. For et fylogenetisk nettverk N Uten søsterretikulasjoner, og har r retikulerte hjørner Og med bladsett X, betegner Vi T ( N ) Som settet av alle trær som finnes I N. Hvert slikt tre oppnås ved å følge to trinn: (1) for hvert retikulert toppunkt, fjern en av de innkommende kantene, og deretter (2) for hvert toppunkt v av indegree og outegree 1, hvis foreldre er u og barn er w, kontrakt kantene (u, v) og (v, w) i en enkelt kant (u, w). Betingelsen om at hver kant I N har et tre-toppunkt som et endepunkt, og at hvert tre-toppunkt har minst ett tre-toppunkt som barn, sikrer at settet av blader av det resulterende treet er det samme som nettverket. Derfor inneholder settet T (N ) nøyaktig 2rylogenetiske trær hvis bladsett er nøyaktig X.

   Maksimal Parsimoni

   vi henviser leserne til for en generell beskrivelse av ideen om parsimoni og til diskusjonen av ulike parsimonialgoritmer. Det har blitt påpekt ved at parsimony-metoden for trær kan utvides til fylogenetiske nettverk. I en rekke artikler, er en slik parsimony kriterium definert ved å finne et tre i nettverket som har den beste parsimonious score, og effektive algoritmer for å optimalisere dette kriteriet på en gitt fylogenetisk nettverk har blitt utviklet. Selv om disse algoritmene er vist å fungere godt i praksis, kan de utføre riktig bare for fylogenetiske nettverk uten søsterretikulasjoner, siden det er greit å søke etter et optimalt tre i denne begrensede klassen av nettverk. I denne delen oppgir vi en alternativ versjon av parsimonyproblemet, og i de følgende avsnittene gir vi noen heuristiske løsninger for å optimalisere poengsummen på et fylogenetisk nettverk.

   La = {1, 2, …, n} angi settet med bladetiketter av et gitt fylogenetisk nettverk N. en funksjon λ: → {0, 1,…|| Σ / – 1} kalles en statlig oppdragsfunksjon over alfabetet Σ (et ikke-tomt sett) For N. Vi sier at en funksjon λ ^ :V (N ) → { 0 , 1 , … , | Σ / – 1 } er en forlengelse av λ på n hvis den er enig med λ For et toppunkt v i N kaller Vi λ ^ (v) som en tildeling av λ ^ på v. et fullt tildelt nettverk er et nettverk der alle toppunktene har etiketter fra {0, 1,…, |Σ| – 1}. La C være en kostnadsmatrise hvis ijth-oppføring c ij er kostnaden ved å transformere fra stat i til stat j langs en hvilken som helst kant i N. hvis e = (u, v) er en kant i n, hvor u er overordnet til v, betegner vi w e ( λ ) ^ = c i j , hvor i= λ ^ ( u ) og j= λ ^ ( v ) . For en graf G lar Vi E (G) betegne kantsettet G. da er parsimonyproblemet definert som følger.

   Inngang: Et fylogenetisk nettverk N med blad etiketter og en statlig oppgave funksjon λ over alfabetet Σ for N.

   Parsimony kriterium: For en utvidelse λ ^ av λ, la

   P 1 ( λ ^ ) = min T ∈ T ( N ) ∑ e ∈ E ( T ) w e ( λ ^ ) ,

   og

   P 2 ( λ ^ ) = ∑ e ∈ E ( N ) w e ( λ ^ ) .

   Utgang: Gitt P ∈ {P1, P2}, finn λ ^ som minimerer P (λ ^ ) .

   Vi merker Oss At P 1 (λ ^) er introdusert i Og P 2 (λ ^ ) er definisjonen vi vil bruke i denne artikkelen. En mer generell tilnærming er å minimere Q ( λ ^ ) = ∑ e ∈ e ( n ) d e ( w e ( λ ^ ) ) , hvor d e er en ikke-negativ vektfunksjon på kantene Av N. I denne artikkelen begrenser vi Oss til P = P2, selv om den første av våre tilnærminger, inneholder den dynamiske programmeringsløsningen også For P = Q.

   parsimonialgoritmer på nettverk

   Krysser et fylogenetisk nettverk

   I et nettverk, vertex traversal refererer til prosessen med å besøke hvert toppunkt, akkurat En Gang, På En Systematisk Måte. Slike traversaler er klassifisert etter rekkefølgen der kryssene blir besøkt. Vi trenger to typer nettverk vertex traversals for å beskrive våre algoritmer. Disse er kjent for fylogenetiske trær, og vi presenterer dem her for fylogenetiske nettverk. Algoritmene for traversalene som er gitt nedenfor, starter fra et gitt vertex v i nettverket. I dette papiret vil vi alltid utføre traversalene fra rotens toppunkt i nettverket.

   Pre-order traversal av et fylogenetisk nettverk fra et vertex v

   1. Besøk vertex v.

   2. Rekursivt utfør pre-order traversal fra hvert barn som ennå ikke er besøkt.

   post-order traversal av et fylogenetisk nettverk fra et vertex v

   1. Rekursivt utføre post-order traversal fra hvert barn som ennå ikke er besøkt.

   2. Besøk vertex v.

   Siden et fylogenetisk nettverk er EN DAG, vil slike traversaler besøke alle hjørner av nettverket nøyaktig en gang. (Se for mer informasjon om eksistens på slike traversaler på DAGs). I forbindelse med dette papiret antar vi at kryssene i et nettverk er unikt merket av heltall. Merk at bladene allerede er merket fra settet ; og så bruker vi andre heltall for andre hjørner. Når barnet hjørnene av v er ekstrahert, de er også anordnet i økende rekkefølge av deres heltall etiketter og pre-og post-order traversals er utført i denne rekkefølgen. Dette vil sikre følgende: hvis toppunktene v og v ‘er slik at det ikke er noen rettet bane mellom dem, blir toppunktet v krysset før toppunktet v’ i forhåndsbestillingen hvis og bare hvis toppunktet v krysses før toppunktet v ‘ i postordren. Se Figur 1 for noen eksempler. Med denne egenskapen merker vi at pre – og post-order traversals fra roten til et fylogenetisk nettverk hvert spor det samme spenntreet, som vi kaller her traversaltreet.

   Dynamisk Programmeringsløsning

   Dynamisk programmering brukes til å gi effektive løsninger for å finne den eksakte parsimony score når nettverket er et fylogenetisk tre . I denne delen viser vi at samme tilnærming kan generaliseres til fylogenetiske nettverk. Sankoffs algoritme på et tre krysser treets hjørner via postordre mens de beregner minimumskostnadene for hver stat ved hvert toppunkt fra bladene til roten, og velger deretter de beste oppdragene på hvert toppunkt ved å backtracking fra roten til bladene ved å krysse treets toppunkter via forhåndsbestilling. Begge fasene presenteres for nettverk i Henholdsvis Algoritmer 1 og 2. Vi beskriver dem kort nedenfor. Det kan bemerkes at hvis nettverket er et tre, samsvarer våre algoritmer med pre-order og post-order faser Av Sankoffs metode for trær.

   Gitt Et fylogenetisk nettverk N, med bladkryss merket og med statlig oppdragsfunksjon λ over alfabetet Σ, tildeler hvert toppunkt v ∈ v et antall S v (i) For hver i ∈ σ. I fylogenetiske trær betegner S v (i) den minste summen av kostnadene for alle hendelsene fra toppunktet v til alle bladene som kan nås fra v, gitt at v er tildelt tilstand i og alle etterkommerne fra v er hver tildelt en tilstand. I nettverk er det ingen enkel måte å beregne en slik mengde på. I stedet tillater Vi S v (i) å være en lavere grense av den ovennevnte eksakte poengsummen, og den beregnes i postordrefasen.

   post-order traversal fase: hvis v er et blad Av N, blir S v (i) tildelt 0 hvis den observerte tilstanden er tilstand i, og uendelig ellers. Nå er alt vi trenger et rekursjonsforhold for å beregne S v (i) for resten av kryssene. For hvert barn w av v, vi sier w tilfredsstiller post-order traversal tilstand med hensyn til v, eller bare traversal tilstand med hensyn til v i lys av observasjonen i begynnelsen av denne delen, hvis følgende hold:

   (i)

   vertexet w er et retikulert vertex og

4. (ii)

   hvis v’ er forelder til w annet enn v, må vertexet v krysses før v’ i Postordren traversering Av N.

vi definerer nå rekursivt for hver kant (v, w),

s ( v , w ) ( i ) = min j hvis w tilfredsstiller traversal tilstanden med hensyn til v ; min j c i j ellers . for et fylogenetisk tre antar s(v, w)(i) alltid den første av disse mengdene, og det gir dermed summen av substitusjonskostnadene langs kantene av treet som ligger under toppunktet v, forutsatt at toppunktet v er tildelt tilstanden i. konto for alle substitusjonskostnadene langs alle kantene som ligger under V. På den annen side, hvis v ikke er forelder for w i traversaltreet, betegner s(v, w)(i) bare substitusjonskostnaden fra stat i ved vertex v til en annen stat ved w som er minst dyr.

vi definerer

S v (i ) = ∑ w s ( v , w) (i ) ,

(1)

hvor summen går for alle barn(ren) vertex (s) w av v. Som nevnt tidligere, I fylogenetiske trær, betegner S v (i) den minste mulige summen av substitusjonskostnader langs alle kantene fra toppunktet v til alle bladene som kan nås fra v, gitt at v er tildelt tilstand i og alle toppunktene som kan nås fra v er hver tildelt en tilstand.

i fylogenetiske nettverk, mens beregning av s(v, w)(i) hvor w er et retikulært toppunkt slik at (v, w) ikke er en kant i traversaltreet, er det ingen forkunnskaper om tilstanden som senere vil bli tildelt ved det retikulære toppunktet w. Begrunnelsen for dette er at s (v, w) (i) er substitusjonskostnaden fra stat i ved vertex v til en annen stat ved w som er minst kostbare, i stedet for substitusjonskostnaden fra stat i ved v til staten ved w som senere vil bli tildelt. Siden definisjonen Av S v (i) avhenger av definisjonen av s (v, w) (i), og de er definert rekursivt, observerer vi følgende: S v (i) er en nedre grense på summen av substitusjonskostnader langs kantene av nettverket som kan nås fra toppunktet v, forutsatt at v er tildelt tilstand i og alle etterkommer tre hjørner er tildelt en unik tilstand, og retikulerte hjørner er tildelt to tilstander som ikke nødvendigvis er de samme. De tildelte tilstandene til det retikulerte toppunktet bidrar til en konflikt hvis tilstandene ikke er de samme. La oss anta at staten i er tildelt rot vertex r, og alle tre toppunkter er tildelt en unik tilstand, mens de retikulære toppunktene er tildelt to stater. Deretter angir kostnaden S r (i) den minste mulige summen av substitusjonskostnader langs alle kantene av et traversaltre med en av tilstandene tildelt for retikulerte hjørner, pluss summen av substitusjonskostnadene langs de resterende retikulerte kantene med den alternative tildelingsstaten ved retikulerte hjørner. Siden vi søker en oppgave på nettets hjørner uten konflikter i retikulerte hjørner, Er S r (i) en lavere grense på kostnaden for en slik oppgave der rottepunktet er tildelt i og alle hjørner er tildelt med en unik oppgave.

i denne fasen lagrer vi også tilstandene

t ( v, w) (i ) = a r g min j hvis w tilfredsstiller traversal tilstanden med hensyn til v; a r g min j c i j ellers .

(2)

for å kunne backtrack tilstanden til w som oppnår mengden s(v, w) (i) under forhåndsbestillingsfasen. Se Algoritme 1.

pre-order traversal phase: vi velger først minimum

S= min I S r ( i )

hvor r er roten vertex og tilordne staten som oppnår minimum ved roten vertex, dvs., la λ ^ (r ) = i r slik At S r (i r ) = S. for ethvert annet toppunkt w som ikke er et retikulert toppunkt, hvis foreldre v allerede er tildelt en tilstand i, tilordner vi staten t(v, w) (i). For et retikulert toppunkt w hvis overordnede toppunkter er v og v’, la oss anta at v og v’ er tildelt stater i og i ‘ henholdsvis når de krysser av forhåndsbestillingen. De mulige tilstandene j = t(v, w)(i) og j’ = t(v’, w)(i’) av w som oppnår henholdsvis s(v, w)(i) og s(v’, w)(i’), trenger ikke å være de samme. Med andre ord er det mulig at j ≠ j’. I dette tilfellet har vi en konflikt på det retikulerte toppunktet w. dermed gir den dynamiske programmeringsteknikken ikke en forlengelse for λ hvis parsimoni-poengsum Er S. I dette tilfellet velger vi bare mellom j og j’ for λ (w) i henhold til hvilken av toppunktene mellom v og v’ krysses først i forhåndsbestillingen. Dermed, hvis toppunktet w tilfredsstiller traversale tilstanden med hensyn til v, har vi λ ^ ( w ) =j.

etter å ha fullført forhåndsbestillingsfasen, kan vi få poengsummen som svarer Til forlengelsesfasen ^ ved første innstilling S’ = S og oppdatering S ‘ ved hvert retikulert toppunkt w som følger: Den øvre bundne poengsummen S ‘oppdateres tilsvarende oppdraget j på vertex w som S’ – c i ‘ j ‘+c i ‘ j . Se Algoritme 2. Figur 2 viser et eksempel på hvordan algoritmen kjører på et nettverk. Siden S r (i) er en nedre grense på det optimale oppdraget hvor rottepunktet er tildelt i og alle hjørner er tildelt med en unik oppgave, og siden s = min I S r (i), konkluderer Vi at S er en nedre grense av det optimale vi søker å finne. Se Lemma 1 for et formelt bevis.

Dynamisk programmeringsløsning. Den dynamiske programmeringsløsningen brukes på et fylogenetisk nettverk. Statene er 0, 1 og 2. Kostnadsmatrisen som brukes har alle 1s unntatt diagonale elementer som er alle 0s. tabellene som vises på hvert toppunkt v er kostnadene, S v (i) (andre rad) av hver stat, i (første rad) som beregnes under post-order traversal. Også vist ved hjørnene er tilstandene til barnet w, nemlig t(v, w) (i) (tredje rad)som tilsvarer kostnadene i andre rad; når det er to barn for et toppunkt, er oppføringene i tredje rad representert som et par tilstander til venstre barn og høyre barn henholdsvis. Hver kant(v, w) er merket med s(v, w) (i) for hver tilstand i. Under pre-order traversal, statene for hvert toppunkt er valgt (vist i fet skrift). Kostnaden for 2 uthevet i fet skrift ved roten vertex gir en nedre grense, S. staten tildelt på hvert toppunkt er uthevet i fet skrift. Algoritmen finner totalt tre substitusjoner (uthevet av dristige kanter). Dette skyldes at tilstandene som er tildelt ved det retikulerte toppunktet, gir motstridende oppgaver på henholdsvis 1 og 2, hvorav tilstand 1 er tildelt ved retikulert toppunkt. Dermed med en ekstra kostnad på 1, får vi score på 3 (en øvre grense av optimal score) som parsimony score tilsvarende oppdraget vist. Legg merke til at den optimale parsimony-poengsummen på nettverket er 2 (lik den nedre grensen), som kan bli funnet ved uttømmende søk og kan realiseres ved å endre oppdraget fra 1 til 2 for venstre forelder av retikulert toppunkt og fra 1 til 2 for retikulert toppunkt. Dermed samsvarer den nedre grensen med optimal score, selv om oppdraget som svarer til den nedre grensen ikke er konfliktfritt og ikke det samme som oppdraget som svarer til det optimale.

Lemma 1. Mengden S er en nedre grense for optimal parsimony score På nettverket N.

Bevis. Ved bygging av S, har vi

hvor den andre summand er for reticulate vertex w med foreldre er v og v’, slik at v tilfredsstiller traversal tilstand w.r.t. w. Dermed kostnaden c λ ^ ( v ) , λ ^ ( w ) er byttet koster fra det tildelte statlige λ ^ ( v ) på v til staten λ ^ ( w ) på w. På den annen side, kostnaden c λ ^ ( v ‘) , t ( v , w ) ( λ ^ ( v ‘) ) er byttet koster fra det tildelte statlige λ ^ ( v ) på v til staten-t ( v , w ) ( λ ^ ( v ‘ ) ) på w. Merk at staten t ( v , w ) ( λ ^ ( v ‘ ) ) er ikke nødvendigvis samme som staten λ ^ ( w ) , og S er det minste blant alle oppdrag som kan resultere i konflikter på reticulate knutepunktene.

Anta At s ^ er den optimale parsimony-poengsummen På N med funksjonen μ: V (N) → {0, 1, …, / Σ / – 1} som forlengelse av λ har vi

hvor i den andre summand w er et retikulert vertex med foreldre v og v’. Siden μ er en konfliktfri oppgave som finnes i settet av alle oppdrag, hvorav kostnadene S er minimum (sammenlign ligning (3) og (4)), har Vi S≤ s^. □

Nå for kompleksiteten av algoritmen. Anta at nettverket N har n blader og r retikulere hjørner. Da er antall hjørner I N 2 (n + r) -1. Ved hvert toppunkt v og for hver stat i kan mengden S beregnes I O (k2) tid, hvor k = / Σ/. Pre-order traversal-trinnet innebærer å finne S I O (k) kompleksitet og tildele de beste tilstandene for hvert toppunkt. Også å fikse motstridende retikulerte vertex-tilstander tar O (r) tid. Således kompleksiteten av algoritmen (presentert her) for å finne en nedre og en øvre grense Er O ((n + r) k2). En alternativ øvre grense kan oppnås I O (nk2) ved ganske enkelt å tildele I løpet av postordrefasen, for hvert retikulert toppunkt tilstanden som oppstår maksimalt antall ganger på bladene som kan nås fra det respektive retikulerte toppunktet; og fortsetter via å finne S v (i) for de gjenværende toppunktene. Det nøyaktige optimale kan også oppnås ved å begrense de mulige tilstandene til en enkelt tilstand for hvert retikulert toppunkt, ved å kjøre den dynamiske programmeringsalgoritmen for hver av kr-kombinasjonene av tilstander for retikulerte hjørner, og velge minimum blant dem alle. Tidskompleksiteten til denne prosessen Er O (nkr+2).

Algoritme 1 post-order traversal fase: Beregn kostnadene for hver stat på hvert toppunkt

1. 1:

   Input: Nettverk N og de observerte tilstander Fra Σ ved bladene Av N, dvs.en statlig oppgave funksjon λ over alfabetet Σ for N.

2. 2:

   for hvert blad v, la S v (i) = 0 hvis λ(v) = i og ∞ ellers.

3. 3:

   Gjenta i post-rekkefølge for hver i internt vertex (rot, internt tre vertex eller retikulert vertex) v I N: For hver tilstand i, beregne S v (i) gitt i (1) og t(v, w) (i) for hvert barn w av v, gitt i (2).

4. 4:

   Utgang: {(S v (i),): v ∈ V (N), i ∈ σ}.

Minimerer antall mutasjoner på et fylogenetisk nettverk

Fitch-algoritmen teller antall endringer i et bifurcerende fylogenetisk tre for et hvilket som helst tegnsett, hvor tilstandene kan endres fra hvilken som helst tilstand til hvilken som helst annen tilstand. Dermed er kostnadsmatrisen slik at dens diagonale elementer er alle nuller og de diagonale elementene er alle. I denne delen viser Vi Hvordan Fitchs algoritme strekker seg til å finne øvre og nedre grenser for antall evolusjonære endringer i et gitt fylogenetisk nettverk. Først viser Vi At Fitch-algoritmen kan utvides for å gi en øvre grense for optimal parsimoni-poengsum. Som tidligere er postordre og pre-order traversale faser gitt i Algoritmer 3 og 4 nedenfor. Se Figur 3 for et eksempel på algoritmen.

Løsning Av Fitch-type. Fitch-type løsning brukes på samme fylogenetisk nettverk og blad data I Figur 2. Hvert toppunkt er tildelt et sett med alle mulige tilstander, sammen med en poengsum når nettverkspunktene krysses i postordre. Poengsummen ved roten gir en øvre grense for optimal poengsum. Statens oppdrag er gitt i pre-order traversal-fasen, og antall substitusjoner samsvarer med poengsummen ved roten.

Algoritme 2 pre-order traversal fase: Beregn nedre og øvre grenser for optimal og tilsvarende tildeling av øvre grense

1. 1:

   Inngang: {(S v (i), ): v ∈ V (N), i ∈ σ}.

2. 2:

   La S = min I S r (i), hvor r er roten vertex og la λ ^ ( r) =arg min I S r ( i ) .

3. 3:

   La S ‘ = S

4. 4:

   for hvert toppunkt w i forhåndsbestilling hvis overordnede toppunkt v umiddelbart går foran w i forhåndsbestillingen, la λ ^ ( ω ) = t v , w ( i ) , hvor jeg= λ ^ ( v ) .

5. 5:

   Besøk hvert retikulere toppunkt w med foreldre v og v’ slik at w tilfredsstiller traversale tilstanden med hensyn til v, med i= λ ^ ( v ) , i ‘= λ ^ ( v ‘) , j ‘= t ( v ‘, w ) ( i ) og oppdater S’ som følger:

   S ‘← S ‘- c i ‘ j ‘+ c i ‘ j .
6. 6:

   Utgang: (Nedre grense, Øvre grense) = (S, S’); forlengelse som svarer Til øvre grense score S’: λ ^ .

Algoritme 3 Post-order traversal fase: Beregne den optimale

1. 1:

   Inngang: Fylogenetisk nettverk N Og en tilstandsoppdragsfunksjon λ over alfabetet Σ for N.

2. 2:

   for hvert blad v av N får Vi A(v) = {λ (v)}, et singleton sett som inneholder den observerte tilstanden på bladet.

3. 3:

   Sett UB = 0.

4. 4:

   Recurse ved hjelp av post-order: for et toppunkt v Av T med barn w1 og w2, la og hvis toppunktet v har et enkelt barn w, så

og