Sannsynlighet Og Statistikk > Normalfordelinger
Innhold:
- Hva Er En Normalfordeling?
- Den Vanlige Normalmodellen
- Normalfordelingsordproblemer.
- Normalfordeling på TI 89 Eksempler
- Relaterte Artikler.
- Hva Er En Normalfordeling?
- Egenskaper for en normalfordeling
- Standard Normal Modell: Distribusjon av Data
- Praktiske Anvendelser av Standard Normal Modell
- Sannsynlighetsspørsmål ved Hjelp Av Standardmodellen
- Standard normalfordeling: Hvordan Finne Sannsynlighet (Trinn)
- Normalfordeling Ord Problemer
- «Mellom»
- Ordproblemer med normalfordeling: «Mellom»: Trinn
- «Mer enn «eller»Over»
- Less Than
- normalfordeling av ordproblemer mindre enn: Trinn
- Lavere Cut Off
- Normalfordeling TI 89 Eksempler
- Finne Cut Off Poeng For En Topp Prosent
- Eksempel På Sannsynlighetsandel (NormalCDF-funksjon)
- TI-89 Grafer En Normalfordelingskurve
Hva Er En Normalfordeling?
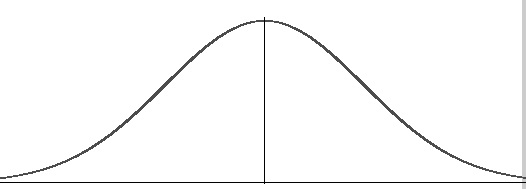
en normalfordeling.en normalfordeling, noen ganger kalt klokkekurven, er en fordeling som forekommer naturlig i mange situasjoner. For eksempel er klokkekurven sett i tester som SAT og GRE. Hovedtyngden av studentene vil score gjennomsnittet (C), mens mindre antall studenter vil score En B Eller D. en enda mindre andel av elevene scorer En F Eller En A. dette skaper en fordeling som ligner en bjelle (derav kallenavnet). Klokkekurven er symmetrisk. Halvparten av dataene vil falle til venstre for gjennomsnittet; halvparten vil falle til høyre.
Mange grupper følger denne typen mønster. Det er derfor det er mye brukt i næringslivet, statistikk og i offentlige organer SOM FDA:
- Høyder av mennesker.
- Målefeil.
- Blodtrykk.
- Peker på en test.
- IQ score.
- Lønn.
den empiriske regelen forteller deg hvilken prosentandel av dataene dine som faller innenfor et visst antall standardavvik fra gjennomsnittet:
• 68% av dataene faller innenfor en standardavvik av gjennomsnittet.
• 95% av dataene faller innenfor to standardavvik fra gjennomsnittet.
• 99,7% av dataene faller innenfor tre standardavvik fra gjennomsnittet.
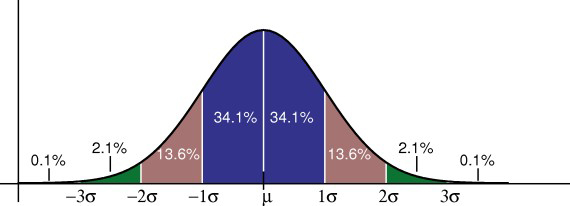
standardavviket styrer spredningen av fordelingen. Et mindre standardavvik indikerer at dataene er tett gruppert rundt gjennomsnittet; normalfordelingen vil være høyere. Et større standardavvik indikerer at dataene er spredt rundt gjennomsnittet; normalfordelingen blir flatere og bredere.
Egenskaper for en normalfordeling
- gjennomsnitt, modus og median er alle like.
- kurven er symmetrisk i midten (dvs. rundt gjennomsnittet, μ).
- nøyaktig halvparten av verdiene er til venstre for sentrum og nøyaktig halvparten av verdiene er til høyre.
- det totale arealet under kurven er 1.
Standard Normalmodellen
en standard normalmodell er en normalfordeling med et gjennomsnitt på 0 og et standardavvik på 1.
Standard Normal Modell: Distribusjon av Data
en måte å finne ut hvordan data distribueres er å plotte dem i en graf. Hvis dataene er jevnt fordelt, kan du komme opp med en klokkekurve. En klokkekurve har en liten prosentandel av punktene på begge haler og den større prosentandelen på den indre delen av kurven. I standard normal modell vil omtrent 5 prosent av dataene dine falle inn i «haler» (farget mørkere oransje i bildet nedenfor) og 90 prosent vil være i mellom. For eksempel, for testresultater av studenter, vil normalfordelingen vise at 2,5 prosent av studentene får svært lave score og 2.5 prosent får svært høy score. Resten vil være i midten; ikke for høy eller for lav. Formen på standard normalfordeling ser slik ut:
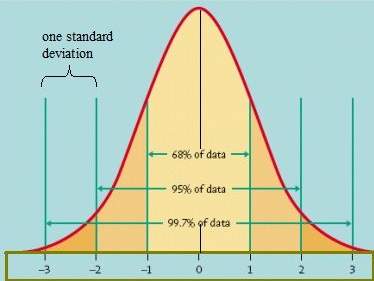
Standard normal modell. Bilde kreditt: University Of Virginia.
Praktiske Anvendelser av Standard Normal Modell
standard normalfordeling kan hjelpe deg med å finne ut hvilket emne du får gode karakterer i og hvilke fag du må utøve mer innsats på grunn av lave scoring prosenter. Når du får en poengsum i ett emne som er høyere enn poengsummen din i et annet emne, kan du tenke at du er bedre i emnet der du fikk høyere poengsum. Dette er ikke alltid sant.
du kan bare si at du er bedre i et bestemt emne hvis du får en poengsum med et visst antall standardavvik over gjennomsnittet. Standardavviket forteller deg hvor tett dataene dine er gruppert rundt gjennomsnittet; det lar deg sammenligne forskjellige distribusjoner som har forskjellige typer data-inkludert forskjellige midler.
hvis du for eksempel får en score på 90 I Matte og 95 på engelsk, kan du tro at du er bedre på engelsk enn I Matte. Men I Matte er poengsummen din 2 standardavvik over gjennomsnittet. På engelsk er det bare ett standardavvik over gjennomsnittet. Det forteller deg at i Matte er poengsummen din langt høyere enn de fleste elevene (poengsummen din faller i halen).
Basert på disse dataene, har du faktisk utført bedre I Matte enn på engelsk!
Sannsynlighetsspørsmål ved Hjelp Av Standardmodellen
Spørsmål om standard normalfordeling sannsynlighet kan se alarmerende, men nøkkelen til å løse dem er å forstå hva området under en standard normal kurve representerer. Det totale arealet under en standard normalfordelingskurve er 100% (det er «1» som desimal). For eksempel er den venstre halvdelen av kurven 50%, eller .5. Så sannsynligheten for en tilfeldig variabel som vises i venstre halvdel av kurven er .5.
Selvfølgelig er ikke alle problemer ganske så enkle, og derfor er det et z-bord. Alt et z-bord gjør er å måle disse sannsynlighetene (dvs. 50%) og sette dem i standardavvik fra gjennomsnittet. Gjennomsnittet er i sentrum av standard normalfordelingen, og en sannsynlighet på 50% er lik null standardavvik.
Standard normalfordeling: Hvordan Finne Sannsynlighet (Trinn)
Trinn 1: Tegn en klokkekurve og skygge i området som blir bedt om i spørsmålet. Eksemplet nedenfor viser z >-0.8. Det betyr at du ser etter sannsynligheten for at z er større enn -0,8, så du må tegne en vertikal linje ved -0.8 standardavvik fra gjennomsnittet og skygge alt som er større enn det tallet.
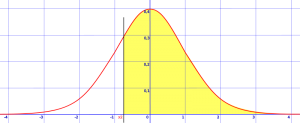
skyggelagt område er z> -0.8
Trinn 2: Gå til indeksen for normal sannsynlighetsområde og finn et bilde som ser ut som grafen din. Følg instruksjonene på den siden for å finne z-verdien for grafen. Z-verdien er sannsynligheten.Tips: Trinn 1 er teknisk valgfritt, men det er alltid lurt å skissere en graf når du prøver å svare på sannsynlighetsordproblemer. Det er fordi de fleste feil skjer ikke fordi du ikke kan gjøre matte eller lese et z-bord, men fordi du trekker en z-score i stedet for å legge til (dvs. du forestiller sannsynligheten under kurven i feil retning. En skisse hjelper deg med å sementere i hodet akkurat det du leter etter.
hvis du fortsatt har problemer, sjekk ut veilederne på Chegg.com. dine første 30 minutter med en live veileder er gratis!
Normalfordeling Ord Problemer
denne videoen viser et eksempel på en normalfordeling ord problem. For flere eksempler, les videre nedenfor:
når du takler normalfordeling i en statistikklasse, prøver du å finne området under kurven. Det totale arealet er 100% (som desimal, det er 1). Normalfordelingsproblemer kommer i seks grunnleggende typer. Hvordan vet du at et ordproblem innebærer normal distribusjon? Se etter nøkkelfrasen «anta at variabelen er normalfordelt «eller» anta at variabelen er omtrent normal.»For å løse et ordproblem må du finne ut hvilken type du har .
- «Mellom»: Inneholder uttrykket «mellom» og inkluderer en øvre grense og nedre grense (dvs. «finn antall hus priset mellom $50k OG 200K»).
- «Mer enn» eller «Over»: inneholder uttrykket «mer enn» eller «over».
- «Mindre enn».
- Nedre Cut Off Eksempel (video)
- Øvre Cut Off Eksempel (video)
Midt Prosent Eksempel (video)
«Mellom»
dette how-to dekker løse problemer som inneholder uttrykket «mellom» og inkluderer en øvre og nedre grense (dvs. «finn antall hus priset mellom $ 50k OG 200K». Merk at dette er forskjellig fra å finne «mellomprosent» av noe.
Ordproblemer med normalfordeling: «Mellom»: Trinn
Trinn 1: Identifiser delene av ordproblemet. Ordet problemet vil identifisere:
- gjennomsnittet(gjennomsnittlig eller μ).
- Standardavvik (σ).
- Valgt Nummer (dvs. «velg en tilfeldig «eller» velg ti tilfeldig»).
- X: tallene knyttet til «mellom» (dvs. «mellom $5000 og $10 000» vil ha X som 5000 og som $10 000).
i tillegg vil DU bli gitt ENTEN:
- Prøvestørrelse (dvs. 400 hus, 33 personer, 99 fabrikker, 378 rørleggere etc.). ELLER
- Du kan bli bedt om en sannsynlighet (i så fall vil prøvestørrelsen din mest sannsynlig være alle, dvs. «Journeyman rørleggere» eller » Førsteårspiloter.»
Trinn 2: Tegn en graf. Sett mener du identifisert I Trinn 1 i midten. Sett tallet knyttet til» mellom » på grafen (ta en gjetning på hvor tallene ville falle–det trenger ikke å være nøyaktig). For eksempel, hvis gjennomsnittet ditt var $100, og du ble bedt om «timelønn mellom $75 og $ 125»), vil grafen din se slik ut:


Trinn 3:Finn ut z-poengene. Plugg den første x-verdien (i grafen min over, den er 75) i z-verdiformelen og løse. Den μ (gjennomsnittet), er 100 fra eksempelgrafen. Du kan få disse tallene (inkludert σ, standardavviket) fra svarene dine i trinn 1 :
![]()
- * Merk: hvis formelen forvirrer deg, er alt denne formelen ber deg om å gjøre:
- trekk gjennomsnittet Fra X
- divider med standardavviket.
Trinn 4: Gjenta trinn 3 for den andre X.
Trinn 5: Ta tallene fra trinn 3 og 4 og bruk dem til å finne området i z-tabellen.
hvis du ble bedt om å finne en sannsynlighet i spørsmålet ditt, går du til trinn 6a. hvis du ble bedt om å finne et tall fra en bestemt gitt utvalgsstørrelse, går du til trinn 6b.
Trinn 6a:
Konverter svaret fra trinn 5 til en prosentandel.
- for eksempel er 0,1293 12,93%.
det er det-hopp over trinn 6b!
Trinn 6b
Multipliser prøvestørrelsen (funnet i trinn 1) med z-verdien du fant i trinn 4. For eksempel, 0,300 * 100 = 30.
Det er det!
«Mer enn «eller»Over»
denne veiledningen dekker å løse normalfordelingsproblemer som inneholder uttrykket » mer enn «(eller et uttrykk som «over»).
Trinn 1: Del opp ordproblemet i deler. Finne:
- gjennomsnittlig (gjennomsnittlig eller μ)
- Standardavvik (σ)
- Et tall (for eksempel «velg femti tilfeldig» eller «velg 90 tilfeldig»)
- X: tallet knyttet til «mindre enn» – setningen. Hvis Du for eksempel ble bedt om å finne «under $9,999», Er X 9,999.
Trinn 2: Finn prøven fra problemet. Du har enten en bestemt størrelse (som «1000 tv») eller en generell prøve («Hver tv»).
Tegn et bilde hvis problemet med gjennomsnittet og området du leter etter. For eksempel, hvis gjennomsnittet er $15, og du ble bedt om å finne hvilke middager som koster mer enn $10, kan grafen din se slik ut:


Trinn 3: Beregn z-poengsummen (plugg verdiene dine inn i z verdi formel og løse). Bruk svarene dine fra trinn 1 :
![]()
I Utgangspunktet er Alt du gjør med formelen å trekke gjennomsnittet fra X og deretter dele det svaret med standardavviket.
Trinn 4: Finn området ved hjelp av z-poengsummen fra trinn 3. Bruk z-tabellen. Ikke sikker på hvordan du leser et z-bord? Se videoen på z-table-siden.
Trinn 6: Gå Til Trinn 6a for å finne en sannsynlighet, eller gå til trinn 6b for å beregne et bestemt tall eller beløp.
Trinn 6a
Gjør trinn 5s svar til en prosentandel.
- for eksempel er 0,1293 12,93%.
Hopp over trinn 6b: du er ferdig!
Trinn 6b
Multipliser prøvestørrelsen Fra Trinn 1 med z-poengsummen fra trinn 4. For eksempel, 0,500 * 100 = 50.
Du er ferdig!
Less Than
denne fremgangsmåten dekker å løse normalfordelingsordproblemer som har uttrykket » less than «(eller et lignende uttrykk som «less than»).
normalfordeling av ordproblemer mindre enn: Trinn
Trinn 1: Del opp ordproblemet i deler:
- gjennomsnittet (gjennomsnittlig eller μ)
- Standardavvik (σ)
- Valgt nummer (dvs. «velg en tilfeldig «Eller»velg ti tilfeldig»)
- X: tallet som går med» mindre enn » (dvs.» under $99,000 » vil liste X som 99,000)
I Tillegg vil DU ha enten:
- en bestemt utvalgsstørrelse. For eksempel 500 båter, 250 smørbrød, 100 tv osv.
- Alle i prøven (du blir bedt om å finne en sannsynlighet). For eksempel «første års medisinstudenter», «Kreftpasienter» eller » Piloter.»
Trinn 2: Tegn et bilde for å hjelpe deg med å visualisere problemet. Følgende graf viser et gjennomsnitt på 15, og et område «under 4»):


Trinn 3: Finn z-verdien ved å koble de oppgitte verdiene til formelen. «X» i utvalgsgrafen vår er 4, og μ (eller gjennomsnitt) er 15. Du kan få disse tallene (inkludert σ, standardavviket) fra svarene dine i trinn 1, der du identifiserte delene av problemet:
![]()
Alt du trenger å gjøre for å løse formelen er:
- Trekk gjennomsnittet Fra X.
- Divider med standardavviket.
Trinn 4: Ta nummeret fra trinn 3, bruk deretter z-tabellen for å finne området.
Trinn 5: for å finne en sannsynlighet, gå til trinn 6a. for å finne et tall fra en bestemt gitt utvalgsstørrelse, gå til trinn 6b.
Trinn 6a
Endre tallet fra trinn 5 til prosent.
- for eksempel er 0,1293 12,93%.
Det er det!
Trinn 6b
Multipliser prøvestørrelsen (funnet i trinn 1) med z-verdien du fant i trinn 4. For eksempel, 0,300 * 100 = 30.
Det er det!
Lavere Cut Off
noen ganger på en normal fordeling ord problem vil du bli bedt om å finne en «nedre grense for en øvre prosentandel» av noe(dvs. «finn cut-off punktet for å bestå en viss eksamen der den øvre 40% av test takers pass»). Et lavere kuttpunkt er punktet der poengene vil falle under det punktet. For eksempel vil du kanskje finne hvor kuttpunktet er for de nederste 10% av testtakerne.
Sjekk Ut Vår YouTube-kanal for flere arbeidede problemer.
Normalfordeling TI 89 Eksempler
i elementær statistikk, vil du ofte bli møtt med et spørsmål som spør deg cut off poeng for en viss prosentandel av normalfordeling, som toppen 90% eller toppen 10%. Mens du arbeider ut disse typer problemer for hånd er tungvint, GJØR ti-89 grafisk kalkulator lett arbeid med å finne cut off poeng for en topp prosent Med Den Inverse Normal funksjon. Hva du faktisk gjør er på jakt etter cut off poeng for en viss persentil: hvis du for eksempel har en liste over karakterer, og du vil vite hvilken poengsum som er på den 99. persentilen, kan du bruke den inverse normale funksjonen til å finne det prosentvise avskjæringspunktet.
Finne Cut Off Poeng For En Topp Prosent
Sample problem: Studenter på et bestemt college gjennomsnitt 5 fot 8 inches (68 inches) høy. Høydene er normalfordelt, med et standardavvik på 2,5 tommer. Hva er verdien som skiller topp 1% av høyder fra resten av befolkningen?
Trinn 1: Trykk PÅ APPER og bruk rulletastene til å markere Stats / List Editor.
Trinn 2: Trykk F5 2 1(dette får deg Til Den Inverse Normale skjermen).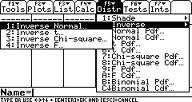
Trinn 3: Skriv inn 0.99 i Området boksen.
Trinn 4: Skriv inn 68 i μ-boksen.
Trinn 5: Skriv inn 2.5 i σ-boksen.
Trinn 6: Trykk PÅ ENTER.
Trinn 7: Les resultatene: Inverse=73.8159 betyr at kutthøyden for den 99. persentilen er 73.8159 tommer.
Det er det!
Eksempel På Sannsynlighetsandel (NormalCDF-funksjon)
Eksempelspørsmål: En gruppe studenter med normalfordelt lønn tjener i gjennomsnitt $6800 med et standardavvik på $2500. Hvor stor andel studenter tjener mellom $6500 og $ 7300?
Trinn 1: Trykk PÅ APPER. Bla til Stats / List Editor og trykk ENTER.
Trinn 2: Trykk På F5 4.
Trinn 3: Skriv inn 6500 i nedre verdi-boksen.
Trinn 4: Skriv inn 7300 i boksen øvre verdi.
Trinn 5: Skriv inn 6800 i μ boksen.
Trinn 6: Skriv inn 2500 i σ-boksen. Trykk ENTER.
Trinn 7: Les svaret. Cdf=.127018. Med andre ord .013, eller 13% av studentene tjener mellom $6500 og $ 7300.
TI-89 Grafer En Normalfordelingskurve
TI-89 kan ikke bare beregne z-score og returverdier for normale fordelinger, det kan også graf normalfordelingskurven. Grafer en normal distribusjon kan hjelpe deg å se hva det er du er ment å være på jakt etter, og gir deg en mer verktøy i å løse normale distribusjonsproblemer. TI-89 kan tegne en normalfordelingskurve med et område skyggelagt for enhver verdi. Du kan for eksempel opprette en graf som er: mindre enn et bestemt tall, større enn et bestemt tall, eller mellom et bestemt sett med tall.
Prøveproblem: Tegn en normalfordelingskurve for studentlønn i løpet av et typisk semester. Studentlønnen har et gjennomsnitt på $ 6800 og standardavvik på $2500. Skygge området på grafen som tilsvarer lønn mellom $ 7,300 og $ 9,000.
Trinn 1: Trykk PÅ APPS og velg Stats / List Editor.
Trinn 2: Trykk På F2 3 Og F2 4.
Trinn 3: Trykk F5 ) 1.
Trinn 4: Rull ned og skriv inn 7300 i nedre verdi-boksen.
Trinn 5: Rull ned og skriv inn 9000 i øvre verdi-boksen.
Trinn 6: Rull ned og skriv inn 6800 i μ-boksen.
Trinn 7: Rull ned og skriv inn 2500 i σ-boksen.
Trinn 8: Rull ned. Slå Automatisk Skala til » ja » ved å trykke på høyre blatast, og deretter ned blatasten for å velge ja. Trykk ENTER.
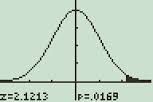
en normalfordeling graf som vises PÅ ti-89 kalkulatoren.
Det er det!
Tips: Hvis du vil legge inn ∞ (uendelig) som en av dine nedre eller øvre verdier, trykker du på diamant-tasten og Deretter Katalog.
Beyer, W. H. CRC Standard Matematiske Tabeller, 28.utg. Boca Raton, FL: CRC Press, s. 533-534, 1987.
Feller, W. En Introduksjon Til Sannsynlighetsteori Og Dens Anvendelser, Vol. 1, 3rd utg. New York: Wiley, 1968.
Kenney, J. F. Og Holde, E. S. Matematikk Av Statistikk, Pt. 2, 2.utg. Princeton, NJ: Van Nostrand, 1951.
Kraitchik, M. » Feilkurven.»§6.4 I Matematiske Rekreasjoner. New York: W. W. Norton, s. 121-123, 1942.Patel, J. K. Og Read, C. B. Håndbok For Normalfordeling. New York: Dekker, 1982.
- Hva Er 68-95-99.7 Regelen?
- Boks Cox Transformasjon
- Boks Muller Transform
- Gaussisk Blanding Modeller.
- Hva er En Normal Sannsynlighet Plot?
- Hvordan Beregne En Z-Score i Statistikk
- Finn området til høyre for en z-score.
- Bruke Normal Tilnærming til å løse Et Binomisk Problem
- Hva er kontinuitetskorrigeringsfaktoren?
- Område Under En Normalfordelingskurveindeks
- Sentralgrenseteorem.
- Den Skjeve Normalfordelingen.
- To Tailed Normal Kurve.
- Q-Funksjonen.
Stephanie Glen. «Normale Distribusjoner (Bell Curve): Definisjon, Ordproblemer» Fra StatisticsHowTo.com Elementær Statistikk for resten av oss! https://www.statisticshowto.com/probability-and-statistics/normal-distributions/
——————————————————————————
Trenger du hjelp med lekser eller test spørsmål? Med Chegg Study kan du få trinnvise løsninger på dine spørsmål fra en ekspert på feltet. Din første 30 minutter med En Chegg veileder er gratis!