Kjetteri kommer i forskjellige nivåer. For den moderne intellektuelle, de laveste nivåene av kjetteri kan være om politikk eller økonomi-områder av tanken der du har lov til å ha uortodokse ideer uten å bli ekskludert fra høflig selskap. Høyere nivåer av kjetteri kan være om religion eller vitenskap-uenig med ortodokse antagelser her, og du vil bli sett på som ganske muligens gal. Det høyeste nivået av kjetteri i den moderne verden er matematisk kjetteri. Uenighet med matematisk ortodoksi er synonymt med «å være en fullverdig sveiv.»Du har rett og slett ikke lov til å tvile på visse ideer i matematikk uten å bli fordømt som en intellektuell spedalsk.Dessverre, Som med ethvert annet tankeområde, er Det Et omvendt forhold mellom «aksept av uenighet» og » sannsynlighet for feil.»Jo mer tabu det er å utfordre en antagelse, jo mer sannsynlig vil det kollapse under granskning. Teologer kan være i stand til å tolerere uenighet Om Guds egenskaper, men de kan ikke tolerere uenighet Om Guds eksistens. Hans eksistens er for grunnleggende til å revidere. Hvis Gud ikke eksisterer, blir hele den teoretiske strukturen bygget på toppen av denne antagelsen ødelagt.
så det er med matematikk. Flere grunnleggende forutsetninger er ikke tillatt å bli utfordret og har derfor blitt til dogmer, noe som gjør denne artikkelen matematisk vranglære.jeg har undersøkt grunnlaget for standard Geometri og funnet to feil – en logisk, den andre metafysiske. Denne artikkelen vil fokusere på det metafysiske. Viktige objekter beskrevet av matematikere eksisterer ikke. Dermed er eventuelle konklusjoner som er avledet basert på eksistensen av disse objektene sannsynligvis feil.i dette tilfellet er den universelt aksepterte påstanden om At «Pi er et irrasjonelt, transcendentalt tall hvis størrelse ikke kan uttrykkes ved endelig desimalutvidelse» falsk på grunn av en metafysisk feil.
Pi Er et rasjonelt tall med endelig desimalutvidelse. Denne ideen, som kan virke utenkelig i begynnelsen, vil vise seg å være overveldende rimelig ved slutten av denne artikkelen.(for resten av denne artikkelen vil jeg forkorte «Pi er et rasjonelt tall med endelig desimalutvidelse» som «Pi er et endelig tall» eller mer enkelt, » Pi er endelig.»)
På Figurer
mine krav er enkle og bevare grunnleggende geometrisk intuisjon. For eksempel er dette en «sirkel»:

Dette er en «linje»:

Og disse er»poeng»:

hvis du tror at disse objektene faktisk er sirkler, linjer og poeng, så tror du også at pi er endelig. Du skjønner, matematikere tror ikke at disse objektene kvalifiserer som «linjer» eller » poeng.»I deres sinn kan linjer og poeng ikke ses, og faktisk vil de si at ovennevnte» linjer og poeng » bare er ufullkomne tilnærminger av linjer og poeng.
For å forstå hvorfor, må vi stille et sett med spørsmål hvis svar folk antar, allerede er sortert ut. Dette er spørsmål som tilsynelatende er så åpenbare at de ikke er verdt å spørre. Og likevel, når vi spør dem om matematikere, får vi tvilsomme svar. Spørsmål som:
Hva er en «form»?
Hva er en «linje»?
Hva er et «punkt»?
Hva er en «sirkel»?
Hva er «avstand»?Spør din gjennomsnittlige intellektuelle disse spørsmålene, og de vil sannsynligvis scoff på deg, fordi de antar, » Alle vet hva en linje er!»De har feil. Jeg, for en, tror ikke at matematikere vet hvilke linjer som er. Og fordi deres teorier er bygget på deres metafysiske påstander om «linjer og poeng», må teoriene revideres fra grunnen av.
Uten Lengde, Bredde eller Forstand
som pi er gjenstand for denne artikkelen, la oss legge ut definisjonen som vi alle har lært i skolen:
Pi Er forholdet mellom en sirkels omkrets og dens diameter.
Vi har noen få nøkkelbegreper her: «forholdet»,» en sirkel»,» omkrets «og»diameter».
for å forstå hva pi er, må vi forstå hva disse andre begrepene betyr. Spesielt denne: «en sirkel.»Her er en definisjon:
en» sirkel » er en form hvis grense består av punkter like langt fra et fast punkt.
Høres rimelig ut. Noen få nøkkelord vi trenger å forstå: «form»,» grense » og » poeng.»Hvis vi ønsker å forstå pi, må vi forstå hva sirkler er, og hvis vi ønsker å forstå hva sirkler er, må vi først forstå hva «poeng» er.det er her jeg finner den grunnleggende feilen som plager ortodoks geometri: definisjonen av et punkt, hvorfra alle andre geometriske objekter er konstruert. Hva er et poeng? Viser seg, det er mange forskjellige definisjoner. Vi starter med Euclids opprinnelige definisjon, som jeg liker.
et «punkt» er det som ikke har noen del.
vi kommer tilbake til den definisjonen senere. Her er en annen:
et «punkt» er en presis plassering eller et sted på et fly.
Ikke dårlig. De er ofte representert av små prikker:

disse intuitive definisjonene er imidlertid ikke brukbare i moderne matematikk. «Poeng», i ortodoks geometri, er egentlig ikke «definert» i seg selv. De skal forstås når det gjelder deres egenskaper. En viktig egenskap er dette:
Poeng har ingen lengde, areal, volum eller andre dimensjonsattributter. De er «nulldimensjonale» objekter.
dette er helt grunnleggende for moderne oppfatninger av geometri. Poeng kan ikke ha noen lengde, bredde eller dybde til dem. Og likevel er alle former tilsynelatende konstruert ut av dem. Så du kan spørre, » Heng på, hvordan kan former, som har dimensjoner, bestå av en haug med punkter som ikke har dimensjoner?»
det er et veldig godt spørsmål, og hvis du insisterer på å finne et logisk svar, vil du ende opp som meg: avvise svært store deler av ortodoks matematikk.
Hver «linje», til en matematiker, er faktisk sammensatt av et uendelig antall poeng – likevel er hvert punkt i seg selv uten noen dimensjon. Linjer, som har lengde, består av punkter, som ikke har lengde. Hvordan gir dette mening?
Det gjør Det ikke.
Det er som å spørre, «Hvor mange 0 må du legge sammen for å få en 1?»Svaret er åpenbart: du kan ikke legge til en haug med 0 sammen og få en 1-ikke engang en uendelig mengde 0. Hvis et punkt har null dimensjoner, spiller det ingen rolle hvor mange du setter sammen. Du vil aldri ende opp med et dimensjonalt objekt. Dette er en logisk nødvendighet.
Så, vi har et veldig stort problem. Det bokstavelige grunnlaget som hele den teoretiske strukturen i moderne geometri er bygget på- «punktet» – er tvilsomt. Feil på dette nivået kan være katastrofale.
Former Uten Form
hvis det er konsistent, tvinger matematikeren seg raskt inn i ulike posisjoner. For eksempel, han må konkludere ting som, » Vi kan ikke se figurer! Ta eksemplet på hva ikke-matematikere kaller en «linje»:

Dette Kan Absolutt Ikke være en linje til en matematiker, fordi linjer angivelig bare har en dimensjonslengde. Dette objektet har både lengde og bredde-det er utvidet i to dimensjoner. Hva kan vi kalle denne formen, da, om ikke en «linje»? Jeg vet ikke – du må spørre en matematiker.
hva med et todimensjonalt objekt: sirkelen?

Sikkert, dette kan Ikke være en sirkel. Dette objektet består av piksler, ikke punkter, og hver piksel er selv utvidet i to dimensjoner. Derfor har objektet grove kanter og er ikke helt glatt. Selv om lekmenn kan kalle det en «sirkel», er det bare en tilnærming til den matematiske sirkelen, noen ganger kalt den » perfekte sirkelen.»
det samme kan sies for det mystiske «punktet»:

disse objektene kan ikke kvalifisere som» poeng » heller, fordi de har dimensjoner. Vi kan se dem, tross alt. Matematiske objekter kan ikke sees; de kan ikke visualiseres; de kan ikke ha noen utvidet – eller» faktisk » – form. Hvis et objekt faktisk har form, hvis det tar opp plass, må det bestå av romlig utvidede objekter som ligner på datamaskinpiksler, ikke matematiske punkter.
Merk: Jeg snakker ikke bare om «fysisk plass» eller «fysisk form». Jeg snakker om former av noe slag. Det jeg ser i mitt synsfelt-fargeblokker – har form – men de er ikke fysiske gjenstander. De selv opptar ikke fysisk plass. De er mentale representasjoner, og de består av utvidede lyspunkter-piksler på min mentale skjerm.
Så oppstår et naturlig spørsmål:
har noen noensinne sett eller opplevd disse matematiske formene på noen måte? Har noen møtt enda en sann «linje » eller»sirkel»? Svaret må være en ettertrykkelig » Nei.»Alle» linjer «og» sirkler » som vi faktisk opplever, har dimensjoner. De er konstruert fra et begrenset antall punkter som selv har dimensjoner. Objektene vi opplever er sammensatt av piksler.
betydningen av dette punktet kan ikke overvurderes.Dette betyr at hver «sirkel» du noensinne har sett-eller noen ingeniør noensinne har lagt ned på papir – faktisk har et rasjonelt forhold mellom omkretsen og diameteren. Hver » sirkel «som noen gang har blitt møtt har en unik» pi » som kan uttrykkes som forholdet mellom to heltall.
«Omkrets», for enhver sirkel vi kan oppleve, kan forstås som «formens ytterste grense», som i seg selv består av et begrenset antall piksler. Det er også «diameter» et enkelt heltall-antall piksler som komponerer det. Sett ett heltall som teller og ett heltall som nevner, og du har en rasjonell pi.
faktisk bør disse sannhetene være ukontroversielle, selv for matematikere:
Hver «sirkel» du noen gang har møtt, uten unntak, har en rasjonell, endelig pi.
Ingen «sirkel» du noen gang har møtt, uten unntak, har en irrasjonell pi.Så det betyr at mine påstander om en «rasjonell pi» er sanne for minst 99,9999% av alle former som vi kaller «sirkler». Det betyr også at pi er unik for en gitt sirkel. Dette bør ikke komme som en overraskelse, men når du tenker på naturen av forholdstall.
Tenk deg at jeg skulle si, » Hva er forholdet mellom bordets høyde og lengde?»
du ville naturligvis svare, » Hvilket bord?»
det samme gjelder for sirkler. Det er ingen «en sann ratio kalt ‘pi ‘»av samme grunn er det ingen» en sann ratio av en tabell høyde til lengde.»Hvert bord og sirkel er konstruert av et begrenset antall enheter, arrangert på forskjellige måter, og derfor vil deres forhold variere.ifølge standardgeometri er det bokstavelig talt bare en » sirkel «som mine påstander ikke gjelder for: den såkalte» Perfekte Sirkelen » -et objekt så mystisk at ingen dødelig noen gang har møtt den.
Den Guddommelige Formen
Denne «perfekte sirkelen» har ingen målbare sider eller kanter. Grensen består av et uendelig antall nulldimensjonale punkter. De ytterste punktene tar opp nøyaktig null plass. Dens pi kan ikke uttrykkes av noen desimalutvidelse – vi vil heller ikke vite nøyaktig hva dens pi er.
dette objektet kan ikke konstrueres, visualiseres eller til og med eksistere i vår verden. Vår verden er for ufullkommen for det. I stedet lever det i et annet rike som våre sinn svakt kan få tilgang til.
Den Perfekte Sirkelen er så stor at alle andre «sirkler» bare er tilnærminger av den. Det er den eneste sanne sirkelen. Hvis du ber om bevis på eksistensen, finner du ingen. Likevel har matematikerne bygget hele sin geometriske teori basert på dens eksistens.
jeg innrømmer fritt min kjetteri: jeg tror ikke på den » perfekte sirkel.»
Derfor tror Jeg ikke på » irrasjonell pi.»Jeg har heller ikke behov for et slikt konsept. Hver form jeg noensinne har møtt – eller noen gang vil møte – har kanter som tar opp plass.
en geometri uten perfekte sirkler, og uten irrasjonell pi, er fullt tilstrekkelig til å forklare alle fenomenene jeg opplever. Derfor har jeg ikke behov for å si en ekstra enhet-spesielt en med slike bemerkelsesverdige egenskaper.
Med andre ord: jeg tror bare på en mindre sirkel enn matematikere. Det er alt som kreves for å konkludere med at pi er et rasjonelt tall for en gitt sirkel.
Bare En Abstraksjon!jeg har hørt noen matematikere hevder at geometriske objekter bare er abstraksjoner og er derfor unntatt fra den foregående kritikken. Men blant annet får dette abstraksjonens metafysikk bakover. Du abstraherer fra betong. Du er ikke konkret fra abstrakt.
Tenk på det. Fra hva gjør man abstrakt for å få begrepet «perfekt sirkel»?
det kan ikke være sirklene vi faktisk ser, siden hver av disse sirklene har ufullkomne kanter. Alle de konkrete opplevelsene vi har er av former med ufullkomne kanter, en rasjonell pi, og består av punkter med dimensjon. Så fra disse erfaringene sier matematikeren: «vel, jeg tror at en ekte sirkel er en uten kanter, med en irrasjonell pi,og består av nulldimensjonale punkter !»
dette er tull, og det er ikke slik abstraksjon fungerer.
Tenk deg at vi snakker om hus og abstrakte forestillinger om hus.
hvert hus vi noen gang har møtt har vegger, et gulv og et tak. Matematikeren vil si at hans oppfatning av et «perfekt hus» er en uten vegger, gulv eller tak. Og faktisk er vanlige gamle hus bare tilnærminger til hans perfekte hus. Tydeligvis er dette en feil.
Vi kan ha en helt gyldig abstrakt oppfatning av et hus, men egenskapene til vårt «abstrakte hus» må inkludere egenskapene til de konkrete husene vi abstraherer fra. Vårt «mentale hus» må inkludere de konseptuelle kategoriene » å ha vegger, gulv og tak.»Dimensjonene til disse egenskapene er irrelevante, sa lenge de eksisterer.en abstrakt oppfatning av «et hus uten vegger, gulv eller tak» kan ikke forklare noen fenomener vi opplever, fordi det beskriver ingen ting som muligens kunne eksistere. Tenk deg at vennen din tar deg til et tomt felt og sier, » Her er mitt perfekte hus! Det har ingen vegger, gulv eller tak!»Du tror han var gal-spesielt hvis han la til,» og alle andre hus er bare en tilnærming til det!»
Ikke Ekte!en av de mer selvinkriminerende svarene fra matematikere går slik: «men matematiske objekter er ikke ekte! De eksisterer ikke i det hele tatt!»I all min forskning kan jeg trygt si at matematikk er det eneste tankeområdet der det å innrømme at» objektene jeg snakker om ikke er ekte og ikke eksisterer » er ment å forsvare en bestemt teori.
denne feilen er en sammenblanding av objekter og deres referanser. For eksempel skal begrepet «mitt hus» referere til » mitt hus i verden.»Det ville være dumt å si «huset mitt tar ikke opp plass, fordi ideen om huset mitt ikke tar opp plass.på Samme måte skal oppfatningen av et «punkt «referere til» en presis plassering i geometrisk rom.»Det ville være like dumt å si» poeng tar ikke opp geometrisk plass, fordi ideen om et punkt ikke tar opp geometrisk plass.»den grunnleggende essensen av geometri handler om rom – enten fysisk rom – mentalt rom, konseptuelt rom eller annen form for rom. Derfor må objektene av geometri selv ta opp plass. Det er ikke noe slikt som » en presis plassering i rommet som ikke er en presis plassering i rommet.»
En Alternativ Teori
Så, la meg presentere et alternativt geometrisk rammeverk. Dette er bare begynnelsen på en helt ny teori om matematikk som jeg kaller » base-unit matematikk.»Dette er grunnleggende for base-enhet geometri:
1) alle geometriske strukturer er sammensatt av basisenheter. Disse enhetene er referert til som » poeng.»
2) hvert punkt er romlig utvidet.
3) i et konseptuelt rammeverk er utvidelsen av basenheten nøyaktig 1. Innenfor denne rammen er det ingen mindre enhet av avstand, per definisjon.
4) alle avstander og former kan betegnes i form av baseenheten.
disse fundamentene danner et logisk godt grunnlag for å bygge geometri.
Sett poeng sammen, og du kan komponere hvilken som helst form du liker, uten irrasjonelle tall. Hvert objekt unntatt baseenheten er et sammensatt objekt, bestående av diskrete punkter. Derfor sa jeg tidligere At Jeg liker Euklids opprinnelige definisjon av et» punkt «som» det som ikke har noen del.»Base-enheter har ingen deler; de er delene som danner alle andre hele.
jeg skjønner at det vil være mange innvendinger mot denne måten å tenke på geometri. Disse innvendingene vil bli behandlet i detalj i fremtidige artikler.
For å få en intuisjon om dette rammeverket, kan du tenke på «poeng» som «piksler», som vi alle har erfaring med. Alle former og objekter du kan støte på i EN hi-res VR-simulering er faktisk klumper av piksler, selv om de kan virke» perfekt glatte » fra vårt makroskopiske perspektiv.
Noen av de fine implikasjonene av denne teorien:
Dette er en linje:

Dette er en sirkel:

og den har en beviselig rasjonell pi:
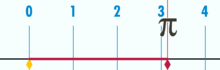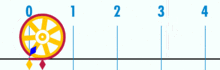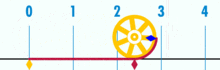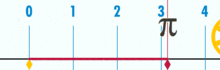
(Merk: DENNE GIFEN ble tatt Fra Wikipedia for å vise pi ‘ s antatte irrasjonalitet. Likevel, hvis du er klar over hva du ser på, er det faktisk en demonstrasjon av rasjonaliteten til pi. Du ser PÅ EN GIF av den logiske perfeksjonen og presisjonen til baseenhetens geometri!)
Hva er forholdet mellom denne sirkelens omkrets og diameter? Enkelt: det er ett heltall over en annen – men mange baseenheter utgjør omkretsen, delt på hvor mange enheter som utgjør diameteren. Og som det skjer, så lenge sirkelen ikke er konstruert fra en liten mengde baseenheter, vil pi-forhold trene til rundt 3.14159 (Selv om vi er helt presise, må vi denominere når det gjelder fraksjoner, da desimalutvidelse kan være tvilsom innenfor en basisenhet. Men det er en fremtidig artikkel.). Det er ingen «generisk» eller «ideell» sirkel. Det er konkrete, faktiske sirkler, som hver er et sammensatt objekt konstruert med et begrenset antall poeng.Dette betyr blant annet at det ikke finnes noe slikt som en «enhetssirkel» – en antatt sirkel med en radius på 1. Det er ingen diametre som har en avstand på 1. Du kan ikke opprette en sirkel med bare en piksel.
Innenfor denne teorien er» sirkler » akkurat det du har møtt. «Poeng» er steder i rommet som er faktiske steder i rommet, og «linjer» er det alle vet de er.Dette emnet Krever Åpenbart mye mer forklaring og arbeid, Ikke bare i geometri, men overalt at metafysikken i matematikk er feil. Jeg kan ikke dekke alle innvendinger mot base-enhet geometri i denne artikkelen, men jeg vil forklare noen flere måter å tenke på det og hvorfor det er bedre enn standard ortodoksi.Først og Fremst forklarer dette rammeverket fullt ut alle fenomenene vi opplever, og det mister nøyaktig null forklaringskraft sammenlignet med standard Geometri. Hver form, hver sirkel, hver linje, hvert punkt, hver romlig opplevelse som vi noensinne vil ha, kan forklares uten å hevde eksistensen av ekstra enheter. Vi opplever ikke perfekte sirkler; derfor har vi ingen grunn til å teoretisere om dem.
videre er baseenhetsmatematikk mer logisk presis enn ortodoksien. Alle som har jobbet med «irrasjonell pi» må bruke tilnærminger. De kan ikke bruke en faktisk uendelig desimalutvidelse. De er tvunget til å vilkårlig kutte av størrelsen for pi for å kunne bruke den. Ikke så med base-enhet geometri. Perfekt presisjon er faktisk mulig, siden det ikke er noen tilnærminger eller uendelige desimalutvidelser å håndtere. Dette er kanskje ikke en stor avtale akkurat nå, men når teknologien nærmer seg baseenhetens dimensjoner av fysisk plass, kan det faktisk gjøre en stor forskjell.
her er en kort, interessant side om pi ‘ s uendelige desimalutvidelse:
Hva skjer når ortodokse matematikere beregner ytterligere og ytterligere desimaler av pi? Er de gripe på «Den Perfekte Sirkelens sanne forhold»? Ingen. Det de gjør er å beregne pi-forholdene for sirkler med stadig mindre baseenheter. Når basenheten krymper – eller når sirkelen blir større i diameter-endres forholdet mellom omkretsen og diameteren litt. Disse beregningene er umiddelbart praktiske, pa samme mate som trig-tabeller er praktiske. De er forhåndsberegnede verdier som er gjeldende og nøyaktige for en gitt sirkel av en gitt størrelse.
(hvis du vil forstå hvorfor pi endres litt, tenk på det på denne måten: når størrelsen på basenheten øker, krymper området som er omsluttet av omkretsen; når størrelsen på basenheten minker, øker området som er omsluttet av omkretsen, men med en avtagende hastighet. Jo jevnere kanten av sirkelen, desto større er sirkelområdet.)
på dette notatet: base-enhet geometri krever ikke en » ultimate base-enhet.»Med andre ord, hver konseptuell ordning vil ha en base-enhet av logisk nødvendighet, men det betyr ikke at du er forhindret i å komme opp med en annen konseptuell ordning som har en mindre baseenhet.
Tenk på det på denne måten: et gitt fotografi vil inneholde et begrenset antall piksler. Det vil ha en base-enhet oppløsning. Det betyr imidlertid ikke at det er umulig å ta et bilde med høyere oppløsning. På Samme måte vil en gitt sirkel ha en baseenhetsoppløsning, Men det betyr ikke at det er umulig å tenke på en med høyere oppløsning (mindre baseenheter).
Vi kan til og med løpe inn i grensene til den fysiske verden. Fysisk plass må ha en base-enhet, noe som betyr at i vårt fysiske system er det ingen mindre enhet. Det betyr imidlertid ikke at vi er forhindret i å snakke om mindre dimensjonale baseenheter. Disse objektene vil ganske enkelt ikke korrelere til vårt univers. Hvem vet-kanskje vi kunne si sanne ting om et annet fysisk univers som har mindre baseenheter.
Merk: Dette korrelerer også perfekt med min oppløsning Til Zenos paradokser. Plassen må ha en base-enhet, hvis bevegelse er mulig.
et godt eksempel på base-unit fenomener er fraktal. Formentlig er fraktaler bare fornuftige innenfor det konseptuelle rammen av » uendelig delbarhet.»Dette er ikke riktig. Fraktaler gir mye mer mening i en base – enhet kontekst. Tenk på dette bildet:

Dette ser ut som en førsteklasses kandidat for » uendelig delbarhet.»Det er imidlertid en illusjon . Til enhver tid, det er en base-enhet oppløsning til dette bildet. Når bildet «zoomer inn», opprettes nye enheter, alle denominert i form av piksler. På ingen måte ser du på uendelig; du ser alltid på et begrenset antall piksler. Hvis du tviler på dette, kan du telle pikslene. Objektet blir konstruert mens du ser det. Det samme skjer i matematikk; objektene blir konstruert som du tenker på dem. Mye mer vil bli sagt om dette i fremtidige artikler.
Polygoner og Greker
jeg vil raskt adressere en innvending som uunngåelig vil oppstå-de som hevder at bildene av sirkler i denne artikkelen egentlig ikke er sirkler; de er polygoner. Kantene er en haug med små rette linjer; de er ikke helt glatte. Hvis dette er sant, er det ingen kritikk av baseenhetens geometri, fordi alle de runde objektene vi møter vil være polygoner. Derfor bør våre matematiske teorier være om polygoner; vi opplever ingenting annet. Jeg vil vite om egenskapene til denne formen:

jeg bryr meg ikke hva du kaller det. Base-enhet geometri kan fortelle deg om egenskapene til den formen.Grekerne gjorde også denne feilen når De snakket om sirkler – som om De var konstruert fra et » uendelig antall linjer.»Dette er feil. Sirkler og polygoner består av et begrenset antall punkter, ikke linjer. Linjer komponerer ikke noe; de er selv sammensatte objekter.
Tenk deg å bygge en sirkel i sanden.

Hva er området i denne sirkelen? Jeg garanterer at det er et begrenset, rasjonelt tall. Du kan bokstavelig talt telle sandkornene som komponerer den. Omkretsen består av sandkorn, som er diameteren, som er området. De er alle heltall.
det siste argumentet jeg vil ta opp i artikkelen kommer fra de som tror at en «sirkel» ikke er en form; det er et matematisk uttrykk. Noe som (x2 + y2 = r2).
dette er bare en annen metafysisk forvirring som samler symboler med objektet symbolene skal beskrive. Det er som å si, «‘Epler’ er synonymt med ordene ‘ en rød frukt.»Dette er forvirret. Ordene «en rød frukt» er en beskrivelse av objektet, ikke selve objektet. Formelen som (x2 + y2 = r2) vil beskrive formen på en sirkel-eller, hvis du foretrekker å tenke på det på denne måten-det er en regel for å bygge en sirkel. Det er ikke i seg selv en sirkel.
det er der jeg skal avslutte denne artikkelen. Det er mye mer å si i fremtiden. Matematikk er ikke unntatt fra kritikk eller skeptisk forespørsel. Det er heller ikke unntatt behovet for presis metafysikk. Av alle grunnene jeg skisserte i dette innlegget, er det god plass til alternative og overlegne oppfatninger av geometri. Baseenhetsgeometri mister ingen forklaringskraft, eliminerer et uendelig antall unødvendige objekter, og gir et logisk grunnlag for å bygge en sterkere teori.Hvis du ikke tror på eksistensen av » perfekte sirkler – – som består av et uendelig antall nulldimensjonale punkter-så tror du ikke at pi er irrasjonell, og du har sluttet deg til en ekstremt liten gruppe intellektuelle spedalske. Du kan nå forvente hån og fordømmelse for din kjetteri.
hvis du likte denne artikkelen og ønsker å støtte etableringen av mer kjetteri, besøk patreon.com/stevepatterson.