BasicsEdit
først noen vokabular:
| aktivering | = tilstand verdi av nevronet. For binære nevroner er dette vanligvis 0 / 1 eller +1 / -1. |
| CAM | = innhold adresserbart minne. Tilbakekalling av et minne med et delvis mønster i stedet for en minneadresse. |
| konvergens | = stabilisering av et aktiveringsmønster på et nettverk. I sl betyr konvergens stabilisering av vekter & forstyrrelser i stedet for aktiveringer. |
| diskriminerende | = relatert til gjenkjenningsoppgaver. Også kalt analyse (I Mønsterteori), eller slutning. |
| energi | = en makroskopisk mengde som beskriver aktiveringsmønsteret i et nettverk. (se nedenfor) |
| generalisering | = oppfører seg nøyaktig på tidligere un-støtt innganger |
| generativ | = Maskin forestilt og tilbakekalling oppgave. noen ganger kalt syntese (I Mønsterteori), etterligning eller dype feil. |
| slutning | = «kjør» – fasen (i motsetning til trening). Under slutning nettverket utfører oppgaven det er opplært til å gjøre—enten gjenkjenne et mønster (SL) eller lage en (UL). Vanligvis kommer slutningen ned i gradienten til en energifunksjon. I motsetning TIL SL skjer gradient nedstigning under trening, IKKE innledning. |
| maskinvisjon | = maskinlæring på bilder. |
| NLP | = Naturlig Språkbehandling. Maskinlæring av menneskelige språk. |
| mønster | = nettverksaktiveringer som har en intern rekkefølge på en eller annen måte, eller som kan beskrives mer kompakt av funksjoner i aktiveringene. For eksempel har pikselmønsteret til null, enten det er gitt som data eller forestilt av nettverket, en funksjon som kan beskrives som en enkelt sløyfe. Funksjonene er kodet i de skjulte nevronene. |
| trening | = læringsfasen. Her justerer nettverket sine vekter & forspenninger for å lære av inngangene. |
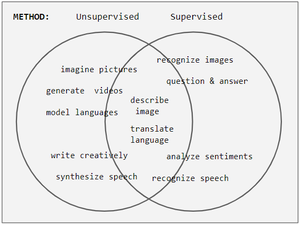
Oppgaver
Energi
en energifunksjon er et makroskopisk mål på et nettverk tilstand. Denne analogien med fysikk er inspirert Av Ludwig Boltzmanns analyse av en gass ‘ makroskopiske energi fra de mikroskopiske sannsynlighetene for partikkelbevegelse p ∝ {\displaystyle \propto }

eE/kT, hvor k er Boltzmannskonstanten og T er temperatur. I rbm-nettverket er forholdet p = e – E / Z, hvor p& e varierer over alle mulige aktiveringsmønstre Og Z = ∑ a L l p a t t e r n s {\displaystyle \sum _{AllPatterns}}

e-E (MØNSTER). For å være mer presis, p (a) = e-E ( a) / Z, hvor a er et aktiveringsmønster av alle nevroner (synlig og skjult). Derfor bærer tidlige nevrale nettverk Navnet Boltzmann-Maskinen. Paul Smolensky kaller-E Harmonien. Et nettverk søker lav energi som er høy Harmoni.
Nettverk
| Hopfield | Boltzmann | Rbm | Helmholtz | Autoencoder | VAE |
|---|---|---|---|---|---|
 |
 |
 restricted Boltzmann machine
|
 |
div boltzmann og helmholtz kom før nevrale nettverk formuleringer, men disse nettverkene lånt fra sine analyser, slik at disse nettverkene bærer sine navn. Hopfield bidro imidlertid direkte TIL UL.
IntermediateEdit
her vil distribusjonene p(x) og q(x) forkortes som p og q.
History
| 1969 | Perceptrons by Minsky & Papert shows a perceptron without hidden layers fails on XOR |
| 1970s | (approximate dates) AI winter I |
| 1974 | Ising magnetic model proposed by WA Little for cognition |
| 1980 | Fukushima introduces the neocognitron, which is later called a convolution neural network. Det er mest brukt I SL, men fortjener en omtale her. |
| 1982 | Ising variant Hopfield net beskrevet som CAMs og klassifiserere Av John Hopfield. |
| 1983 | Ising variant Boltzmann maskin med probabilistiske nevroner beskrevet Av Hinton&Sejnowski følgende Sherington & Kirkpatricks 1975 arbeid. |
| 1986 | Paul Smolensky publiserer Harmoniteori, som er en RBM med praktisk talt samme Boltzmann-energifunksjon. Smolensky ga ikke en praktisk opplæringsplan. Hinton gjorde i midten av 2000-tallet |
| 1995 | Schmidthuber introduserer LSTM neuron for språk. |
| 1995 | Dayan & Hinton introduces Helmholtz machine |
| 1995-2005 | (approximate dates) AI winter II |
| 2013 | Kingma, Rezende, & co. introduced Variational Autoencoders as Bayesian graphical probability network, with neural nets as components. |
Some more vocabulary:
| Sannsynlighet | |
| cdf | = kumulativ distribusjonsfunksjon. integralet av pdf. Sannsynligheten for å komme nær 3 er området under kurven mellom 2,9 og 3,1. |
| kontrastiv divergens | = en læringsmetode hvor man senker energien på treningsmønstre og øker energien på uønskede mønstre utenfor treningssettet. Dette er svært forskjellig FRA KL-divergensen, men deler en lignende ordlyd. |
| forventet verdi | = e(x) = ∑ x {\displaystyle \sum _{x}}
 x * p(x). Dette er middelverdien, eller gjennomsnittsverdien. For kontinuerlig inngang x, erstatt summeringen med et integral. |
| latent variabel | = en uobservert mengde som bidrar til å forklare observerte data. for eksempel kan en influensainfeksjon (ubemerket) forklare hvorfor en person nyser (observert). I probabilistiske nevrale nettverk fungerer skjulte nevroner som latente variabler, selv om deres latente tolkning ikke er eksplisitt kjent. |
| = funksjon for sannsynlighetstetthet. Sannsynligheten for at en tilfeldig variabel tar på seg en viss verdi. For kontinuerlig pdf kan p(3) = 1/2 fortsatt bety at det er nær null sjanse for å oppnå denne eksakte verdien av 3. Vi rasjonaliserer dette med cdf. | |
| stokastisk | = oppfører seg i henhold til en godt beskrevet sannsynlighetstetthetsformel. |
| Thermodynamics | |
| Boltzmann distribution | = Gibbs distribution. p ∝ {\displaystyle \propto }
 eE/kT |
| entropy | = expected information = ∑ x {\displaystyle \sum _{x}}
 p * log p |
| Gibbs free energy | = thermodynamic potential. Det er det maksimale reversible arbeidet som kan utføres av et varmesystem ved konstant temperatur og trykk. fri energi G = varme-temperatur * entropi |
| informasjon | = informasjonsmengden til en melding x = – logg p(x) |
| KLD | = relativ entropi. For probabilistiske nettverk er dette analogen av feilen mellom inngang & etterlignet utgang. Kullback-Liebler divergence (KLD) måler entropiavviket av 1 distribusjon fra en annen distribusjon. Kld(p,q) = ∑ x {\displaystyle \ sum _{x}}
 p * logg (p / q). Vanligvis reflekterer p inngangsdataene, q reflekterer nettverkets tolkning av det, OG KLD reflekterer forskjellen mellom de to. |
Sammenligning Av Nettverk
| Hopfieldth | boltzmann | rbm | helmholtz | autoencoder | vae | |
|---|---|---|---|---|---|---|
| bruk ¬ater | cam, reiser selger problem | cam. Friheten til tilkoblinger gjør dette nettverket vanskelig å analysere. | mønstergjenkjenning (MNIST, talegjenkjenning) | fantasi, etterligning | språk: kreativ skriving, oversettelse. Visjon: forbedre uklare bilder | generer realistiske data |
| neuron | deterministisk binær tilstand. Aktivering = { 0 (eller -1) hvis x er negativ, 1 ellers} | stokastisk Binær Hopfield neuron | stokastisk binær. Utvidet til real-verdsatt i midten av 2000s | binær, sigmoid | språk: LSTM. visjon: lokale mottakelige felt. vanligvis ekte verdsatt relu aktivering. | |
| tilkoblinger | 1-lag med symmetriske vekter. Ingen selvforbindelser. | 2-lag. 1-skjult & 1-synlig. symmetriske vekter. | 2-lag. symmetriske vekter. ingen sideforbindelser i et lag. | 3-lag: asymmetriske vekter. 2 nettverk kombinert til 1. | 3-lag. Inngangen betraktes som et lag, selv om det ikke har inngående vekter. tilbakevendende lag FOR NLP. feedforward konvolutter for visjon. inngang & utgang har samme nevronantall. | 3-lag: inngang, encoder, distribusjon sampler dekoder. sampler anses ikke som et lag (e) |
| slutning & energi | energi er gitt Ved Gibbs sannsynlighetsmål : E = − 1 2 hryvnias i , j w i j s i s j + ∑ i θ i {\displaystyle e=-{\frac {1}{2}}\sum _{i,j}{w_{ij}{s_{i}}{s_{j}}+\sum _{i} {\theta _{i}} {s_{i}}+\sum _{i} {\theta _{i}} {s_ {i}}
 |
← samme | ← samme | minimere kl-divergens | slutning er Bare feed-forward. tidligere ul-nettverk løp FREMOVER og bakover | minimer feil = rekonstruksjonsfeil-KLD |
| trening | Δ = si*sj, for +1/-1 neuron | Δ = e * (pij – p ‘ ij). Dette er avledet fra å minimere KLD. e = læringsrate, p ‘ = forventet og p = faktisk fordeling. | kontrastive divergens w/ Gibbs Sampling | wake-sleep 2 fase trening | tilbake forplante rekonstruksjon feil | reparameterize skjult tilstand for backprop |
| styrke | ligner fysiske systemer slik at den arver sine ligninger | <— samme. skjulte nevroner fungere som intern representasjon av den ytre verden | raskere mer praktisk trening ordningen Enn Boltzmann maskiner | mildt anatomisk. analytisk m/ informasjonsteori & statistisk mekanikk | ||
| svakhet | hopfield | RBM | Helmholtz |
spesifikke nettverk
her fremhever vi noen kjennetegn ved hvert nettverk. Ferromagnetisme inspirerte Hopfield-nettverk, Boltzmann-maskiner og Rbmer. En nevron tilsvarer et jerndomene med binære magnetiske momenter Opp Og Ned, og nevrale forbindelser tilsvarer domenets innflytelse på hverandre. Symmetriske forbindelser muliggjør en global energiformulering. Under slutning oppdaterer nettverket hver tilstand ved hjelp av standard aktiveringstrinn-funksjonen. Symmetriske vekter garanterer konvergens til et stabilt aktiveringsmønster.Hopfield-nettverk brukes Som Kameraer og er garantert å avgjøre seg til et mønster. Uten symmetriske vekter er nettverket svært vanskelig å analysere. Med riktig energifunksjon vil et nettverk konvergere.
Boltzmann maskiner er stokastiske Hopfield garn. Deres tilstandsverdi er samplet fra denne pdf-filen som følger: anta at en binær neuron brenner Med Bernoulli-sannsynligheten p(1) = 1/3 og hviler med p(0) = 2/3. Man prøver fra det ved å ta ET JEVNT fordelt tilfeldig tall y, og plugge det inn i den inverterte kumulative fordelingsfunksjonen, som i dette tilfellet er trinnfunksjonen terskel ved 2/3. Den inverse funksjonen = { 0 hvis x <= 2/3, 1 hvis x > 2/3 }
Helmholtz maskiner er tidlig inspirasjon For Variational Auto Kodere. Det er 2 nettverk kombinert i en-forover vekter opererer anerkjennelse og bakover vekter implementerer fantasi. Det er kanskje det første nettverket som gjør begge deler. Helmholtz jobbet ikke i maskinlæring, men han inspirerte visningen av «statistisk inferens motor hvis funksjon er å utlede sannsynlige årsaker til sensorisk inngang» (3). det stokastiske binære nevronet gir en sannsynlighet for at tilstanden er 0 eller 1. Datainngangen anses normalt ikke som et lag, men I Helmholtz – maskingenereringsmodus mottar datalaget innspill fra mellomlaget har separate vekter for dette formålet, så det regnes som et lag. Derfor har dette nettverket 3 lag.Variational Autoencoder (VAE) er inspirert Av Helmholtz-maskiner og kombinerer sannsynlighetsnettverk med nevrale nettverk. En Autoencoder er et 3-lags CAM-nettverk, hvor mellomlaget skal være en intern representasjon av inngangsmønstre. Vektene heter phi & theta i stedet For W og V som I Helmholtz-en kosmetisk forskjell. Koderneuralnettet er en sannsynlighetsfordeling qφ (z / x) og dekodernettverket er pθ (x|z). Disse 2 nettverkene her kan være fullt tilkoblet, eller bruk en ANNEN nn-ordning.Hebbian Learning, ART, SOM det klassiske eksempelet på uovervåket læring i studiet av nevrale nettverk er Donald Hebbs prinsipp, det vil si nevroner som brenner sammen ledning sammen. I Hebbian læring forsterkes forbindelsen uavhengig av en feil, men er utelukkende en funksjon av tilfeldigheten mellom handlingspotensialene mellom de to nevronene. En lignende versjon som endrer synaptiske vekter tar hensyn til tiden mellom handlingspotensialene (spike-timing-avhengig plastisitet eller STDP). Hebbian Læring har blitt antatt å ligge til grunn for en rekke kognitive funksjoner, for eksempel mønstergjenkjenning og erfaringslæring.Blant nevrale nettverksmodeller brukes selvorganiserende kart (som) og adaptiv resonansteori (ART) ofte i uovervåkede læringsalgoritmer. SOM er en topografisk organisasjon der nærliggende steder i kartet representerer innganger med lignende egenskaper. ART-modellen tillater antall klynger å variere med problemstørrelse og lar brukeren kontrollere graden av likhet mellom medlemmer av samme klynger ved hjelp av en brukerdefinert konstant kalt årvåkenhetsparameteren. KUNSTNETTVERK brukes til mange mønstergjenkjenningsoppgaver, for eksempel automatisk målgjenkjenning og seismisk signalbehandling.
