tehnicile de clasificare sunt o parte esențială a aplicațiilor de învățare automată și de extragere a datelor. Aproximativ 70% din problemele din știința datelor sunt probleme de clasificare. Există o mulțime de probleme de clasificare care sunt disponibile, dar regresia logistică este comună și este o metodă utilă de regresie pentru rezolvarea problemei de clasificare binară. O altă categorie de clasificare este clasificarea multinomială, care se ocupă de problemele în care sunt prezente mai multe clase în variabila țintă. De exemplu, IRIS dataset un exemplu foarte faimos de clasificare multi-clasă. Alte exemple sunt clasificarea articol/blog / document Categorie.
regresia logistică poate fi utilizată pentru diverse probleme de clasificare, cum ar fi detectarea spamului. Diabet predicție, în cazul în care un anumit client va achiziționa un anumit produs sau vor putinei un alt concurent, dacă utilizatorul va Faceți clic pe un link de publicitate dat sau nu, și multe alte exemple sunt în găleată.
regresia logistică este unul dintre cei mai simpli și frecvent utilizați algoritmi de învățare automată pentru clasificarea în două clase. Este ușor de implementat și poate fi folosit ca bază pentru orice problemă de clasificare binară. Conceptele sale fundamentale de bază sunt, de asemenea, constructive în învățarea profundă. Regresia logistică descrie și estimează relația dintre o variabilă binară dependentă și variabile independente.
în acest tutorial, veți învăța următoarele lucruri în regresia logistică:
- Introducere în regresia logistică
- regresia liniară Vs. regresia logistică
- estimarea probabilității maxime Vs. metoda obișnuită cea mai mică pătrată
- cum funcționează regresia logistică?
- construirea modelului în Scikit-aflați
- evaluarea modelului folosind matricea de confuzie.
- avantajele și dezavantajele regresiei logistice
regresia logistică
regresia logistică este o metodă statistică pentru prezicerea claselor binare. Variabila rezultat sau țintă este dihotomică în natură. Dihotom înseamnă că există doar două clase posibile. De exemplu, poate fi utilizat pentru probleme de detectare a cancerului. Se calculează probabilitatea apariției unui eveniment.
este un caz special de regresie liniară în care variabila țintă este de natură categorică. Acesta utilizează un jurnal de Cote ca variabila dependentă. Logistic Regression predicts the probability of occurrence of a binary event utilizing a logit function.
Linear Regression Equation:
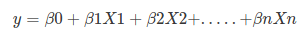
Where, y is dependent variable and x1, x2 … and Xn are explanatory variables.
Sigmoid Function:
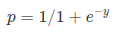
Apply Sigmoid function on linear regression:
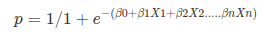
Properties of Logistic Regression:
- variabila dependentă în regresia logistică urmează distribuția Bernoulli.
- estimarea se face prin probabilitate maximă.
- nu R pătrat, modelul de fitness se calculează prin concordanță, KS-statistici.
regresia liniară Vs. regresia logistică
regresia liniară vă oferă o ieșire continuă, dar regresia logistică oferă o ieșire constantă. Un exemplu de ieșire continuă este prețul casei și prețul acțiunilor. Exemplu de ieșire discretă este prezicerea dacă un pacient are cancer sau nu, prezicerea dacă Clientul va putinei. Regresia liniară este estimată folosind cele mai mici pătrate obișnuite (OLS), în timp ce regresia logistică este estimată folosind estimarea probabilității maxime (MLE) abordare.
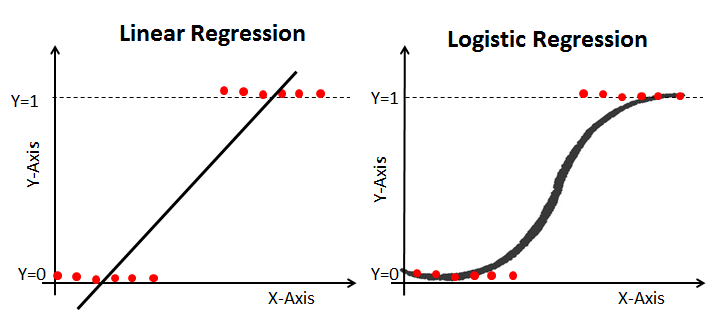
estimarea probabilității maxime Vs. metoda cea mai mică pătrată
MLE este o metodă de maximizare a „probabilității”, în timp ce OLS este o metodă de aproximare care minimizează distanța. Maximizarea funcției de probabilitate determină parametrii care sunt cel mai probabil să producă datele observate. Din punct de vedere statistic, MLE stabilește media și varianța ca parametri în determinarea valorilor parametrice specifice pentru un model dat. Acest set de parametri poate fi utilizat pentru prezicerea datelor necesare într-o distribuție normală.
estimările ordinare ale celor mai mici pătrate sunt calculate prin montarea unei linii de regresie pe punctele de date date care are Suma minimă a abaterilor pătrate (eroarea cea mai mică pătrată). Ambele sunt utilizate pentru a estima parametrii unui model de regresie liniară. MLE presupune o funcție de masă de probabilitate comună, în timp ce OLS nu necesită ipoteze stocastice pentru minimizarea distanței.
funcția sigmoidă
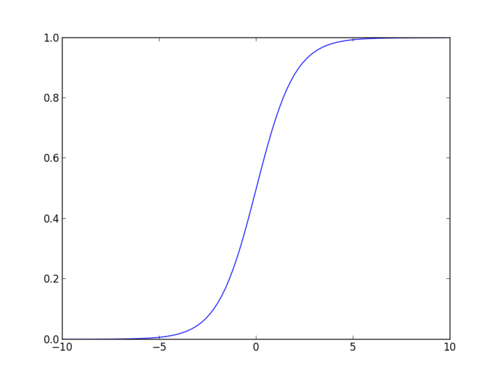
funcția sigmoidă, numită și funcție logistică, oferă o curbă în formă de ‘S’ care poate lua orice număr cu valoare reală și îl poate cartografia într-o valoare cuprinsă între 0 și 1. Dacă curba merge la infinit pozitiv, y prezis va deveni 1, iar dacă curba merge la infinit negativ, y prezis va deveni 0. Dacă ieșirea funcției sigmoid este mai mare de 0,5, putem clasifica rezultatul ca 1 sau da și dacă este mai mic de 0.5, putem clasifica ca 0 sau nu. Rezultatul nu poatede exemplu: dacă rezultatul este de 0,75, putem spune în termeni de probabilitate ca: există o șansă de 75% ca pacientul să sufere de cancer.
tipuri de regresie logistică
tipuri de regresie logistică:
- regresie logistică binară: variabila țintă are doar două rezultate posibile, cum ar fi spam sau nu spam, cancer sau fără cancer.
- regresie logistică multinomială: variabila țintă are trei sau mai multe categorii nominale, cum ar fi prezicerea tipului de vin.
- regresie logistică ordinală: variabila țintă are trei sau mai multe categorii ordinale, cum ar fi restaurantul sau evaluarea produsului de la 1 la 5.
construirea modelului în Scikit-aflați
să construim modelul de predicție a diabetului.
aici, aveți de gând să prezică diabet folosind logistic regresie clasificator.
să încărcăm mai întâi setul de date Pima Indian Diabetes necesar folosind funcția CSV de citire a pandelor. Puteți descărca date de la următorul link:https://www.kaggle.com/uciml/pima-indians-diabetes-database
încărcarea datelor
#import pandasimport pandas as pdcol_names = # load datasetpima = pd.read_csv("pima-indians-diabetes.csv", header=None, names=col_names)pima.head()
selectarea caracteristicii
aici, trebuie să împărțiți coloanele date în două tipuri de variabile dependente(sau variabile țintă) și variabile independente(sau variabile de caracteristici).
#split dataset in features and target variablefeature_cols = X = pima # Featuresy = pima.label # Target variableîmpărțirea datelor
pentru a înțelege performanța modelului, împărțirea setului de date într-un set de antrenament și un set de teste este o strategie bună.
Să împărțim setul de date utilizând funcția train_test_split(). Ai nevoie pentru a trece 3 parametri caracteristici, țintă, și dimensiunea test_set. În plus, puteți utiliza random_state pentru a selecta înregistrări aleatoriu.
# split X and y into training and testing setsfrom sklearn.cross_validation import train_test_splitX_train,X_test,y_train,y_test=train_test_split(X,y,test_size=0.25,random_state=0)/home/admin/.local/lib/python3.5/site-packages/sklearn/cross_validation.py:41: DeprecationWarning: This module was deprecated in version 0.18 in favor of the model_selection module into which all the refactored classes and functions are moved. Also, note that the interface of the new CV iterators is different from that of this module. This module will be removed in 0.20. "This module will be removed in 0.20.", DeprecationWarning)aici, setul de date este împărțit în două părți într-un raport de 75:25. Aceasta înseamnă că 75% date vor fi utilizate pentru formarea modelului și 25% pentru testarea modelului.
dezvoltarea și predicția modelului
în primul rând, importați modulul de regresie logistică și creați un obiect de clasificator de regresie logistică folosind funcția LogisticRegression ().
apoi, se potrivesc modelul pe setul de tren folosind fit() și de a efectua predicție pe setul de testare folosind prezice().
# import the classfrom sklearn.linear_model import LogisticRegression# instantiate the model (using the default parameters)logreg = LogisticRegression()# fit the model with datalogreg.fit(X_train,y_train)#y_pred=logreg.predict(X_test)evaluarea modelului folosind matricea de confuzie
o matrice de confuzie este un tabel care este utilizat pentru a evalua performanța unui model de clasificare. De asemenea, puteți vizualiza performanța unui algoritm. Fundamentalul unei matrice de confuzie este numărul de predicții corecte și incorecte sunt rezumate în clasă.
# import the metrics classfrom sklearn import metricscnf_matrix = metrics.confusion_matrix(y_test, y_pred)cnf_matrixarray(, ])aici puteți vedea matricea de confuzie sub forma obiectului matrice. Dimensiunea acestei matrice este 2 * 2 deoarece acest model este clasificare binară. Aveți două clase 0 și 1. Valorile diagonale reprezintă predicții exacte, în timp ce elementele non-diagonale sunt predicții inexacte. În ieșire, 119 și 36 sunt predicții reale, iar 26 și 11 sunt predicții incorecte.
vizualizarea matricei de confuzie folosind harta termică
să vizualizăm rezultatele modelului sub forma unei matrice de confuzie folosind matplotlib și seaborn.
aici, veți vizualiza matricea de confuzie folosind Heatmap.
# import required modulesimport numpy as npimport matplotlib.pyplot as pltimport seaborn as sns%matplotlib inlineclass_names= # name of classesfig, ax = plt.subplots()tick_marks = np.arange(len(class_names))plt.xticks(tick_marks, class_names)plt.yticks(tick_marks, class_names)# create heatmapsns.heatmap(pd.DataFrame(cnf_matrix), annot=True, cmap="YlGnBu" ,fmt='g')ax.xaxis.set_label_position("top")plt.tight_layout()plt.title('Confusion matrix', y=1.1)plt.ylabel('Actual label')plt.xlabel('Predicted label')Text(0.5,257.44,'Predicted label')
valori de evaluare a matricei de confuzie
să evaluăm modelul folosind valori de evaluare a modelului, cum ar fi precizia, precizia și rechemarea.
print("Accuracy:",metrics.accuracy_score(y_test, y_pred))print("Precision:",metrics.precision_score(y_test, y_pred))print("Recall:",metrics.recall_score(y_test, y_pred))Accuracy: 0.8072916666666666Precision: 0.7659574468085106Recall: 0.5806451612903226Ei bine, ai o rată de clasificare de 80%, considerată o precizie bună.
precizie: precizia înseamnă să fii precis, adică cât de precis este modelul tău. Cu alte cuvinte, puteți spune, atunci când un model face o predicție, cât de des este corect. În cazul tău de predicție, când modelul tău de regresie logistică a prezis că pacienții vor suferi de diabet, că pacienții au 76% din timp.
rechemare: dacă există pacienți care au diabet în setul de testare și modelul dvs. de regresie logistică îl poate identifica 58% din timp.
curba Roc
curba caracteristicii de funcționare a receptorului(Roc) este un grafic al ratei pozitive reale față de rata fals pozitivă. Acesta arată compromisul dintre sensibilitate și specificitate.
y_pred_proba = logreg.predict_proba(X_test)fpr, tpr, _ = metrics.roc_curve(y_test, y_pred_proba)auc = metrics.roc_auc_score(y_test, y_pred_proba)plt.plot(fpr,tpr,label="data 1, auc="+str(auc))plt.legend(loc=4)plt.show()
scorul ASC pentru caz este de 0,86. Scorul ASC 1 reprezintă clasificatorul perfect, iar 0,5 reprezintă un clasificator fără valoare.
avantaje
datorită naturii sale eficiente și directe, nu necesită o putere mare de calcul, ușor de implementat, ușor de interpretat, utilizat pe scară largă de analistul și omul de știință de date. De asemenea, nu necesită scalarea caracteristicilor. Regresia logistică oferă un scor de probabilitate pentru observații.
dezavantaje
regresia logistică nu este capabilă să gestioneze un număr mare de caracteristici / variabile categorice. Este vulnerabil la suprasolicitare. De asemenea, nu poate rezolva problema neliniară cu regresia logistică, de aceea necesită o transformare a caracteristicilor neliniare. Regresia logistică nu va funcționa bine cu variabile independente care nu sunt corelate cu variabila țintă și sunt foarte asemănătoare sau corelate între ele.
concluzie
în acest tutorial, ați acoperit o mulțime de detalii despre regresia logistică. Ați învățat ce este regresia logistică, cum să construiți modelele respective, cum să vizualizați rezultatele și unele dintre informațiile teoretice de fond. De asemenea, ați acoperit câteva concepte de bază, cum ar fi funcția sigmoidă, probabilitatea maximă, matricea de confuzie, curba ROC.
sperăm că acum Puteți utiliza tehnica de regresie logistică pentru a analiza propriile seturi de date. Vă mulțumim pentru citirea acestui tutorial!
Dacă doriți să aflați mai multe despre regresia logistică, urmați cursul Datacamp fundamentele analizei Predictive în Python (Partea 1).