3.3 ciclul Carnot | Maybaygiare.org

următor: 3.4 Frigidere și încălzire: 3. Prima lege anterioară: 3.2 reprezentarea generalizată a conținutului Index

un ciclu Carnot este prezentat în figura 3.4. Are patru procese. Există două picioare reversibile adiabatice și douăpicioare reversibile izoterme. Putem construi un ciclu Carnot cu multe sisteme diferite, dar conceptele pot fi arătate folosind un fluid de lucru familiar, gazul ideal. Sistemul poate fi privit cao cameră închisă de un piston și umplută cu acest gaz ideal.

figura 3.4: ciclul Carnot — diagrama termodinamică din stânga și schema diferitelor etape ale ciclului pentru un sistem compus dintr-un gaz ideal în dreapta

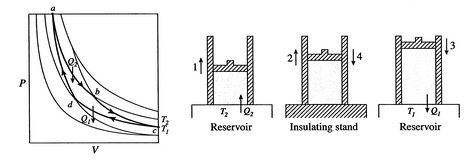
cele patru procese din ciclul Carnot sunt:

sistemul este la temperatura la starea. Este adus în contact cu un rezervor de căldură, care este doar o masă lichidă sau solidă de o măsură suficient de mare, astfel încât temperatura sa să nu se schimbe în mod apreciabil atunci când o anumită cantitate de căldură este transferată în sistem. Cu alte cuvinte, rezervorul de căldură este o temperatură constantăsursă (sau receptor) de căldură. Sistemul suferă apoi o expansiune anizotermică de la la , cu căldură absorbită .
Atstate, sistemul este izolat termic (scos din contactwith rezervorul de căldură) și apoi lăsați să se extindă la. În timpul thisexpansion temperatura scade la . Schimb de căldurăîn această parte a ciclului, $Q_{bc}=0.$ )
la starea sistemul este adus în contact cu un rezervor de căldură la temperatura . Este apoi comprimat la starea 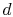, respingând căldura 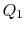în proces.
în cele din urmă, sistemul este comprimat adiabatic înapoi la starea inițială. Schimbul de căldură $Q_{da}=0$ .

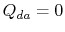eficiența termică a ciclului este dată de definiția

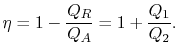$\displaystyle \eta = 1 - \frac{Q_R}{Q_A}=1+\frac{Q_1}{Q_2}.$

(3..4)

în această ecuație, există o convenție semn implicit. Cantitățile așa cum sunt definite sunt mărimile căldurii absorbite șijectate. Cantitățile pe de altă parte sunt definitecu referire la căldura primită de sistem. În acest exemplu, fostul este negativ, iar acesta din urmă este pozitiv. Căldura absorbită șirejectată de sistem are loc în timpul proceselor izoterme șiștim deja care sunt valorile lor din Eq.(3.1):

$\displaystyle Q_2 = w_{ab} =n\mathbf{R}T_2 ,$

$\displaystyle Q_1 = w_{cd} =N\mathbf{R}T_1 =-n\mathbf{r}T_1 .\ quad \ textrm {($Q_1 $ este negativ.)}$

eficiența poate fi acum scrisă în termeni de volume la diferite stări ca

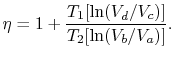$\displaystyle \eta = 1+ \frac{T_1}{T_2}.$

(3..5)

The path from states to and from to are bothadiabatic and reversible. For a reversible adiabatic process we knowthat $PV^\gamma= \textrm{constant}$ . Using the ideal gas equation ofstate, we have $T V^{\gamma-1} = \textrm{constant}$ . Along curve, therefore, $T_2 V_b^{\gamma-1}=T_1 V_c^{\gamma-1}$ . Alongthe curve $T_2 V_a^{\gamma-1}=T_1 V_d^{\gamma-1}$ . Thus,

$\displaystyle \left(\frac{V_d}{V_c}\right)^{\gamma-1} =\frac{(T_2/T_1)}{(T_2/T......right)^{\gamma-1},\textrm{ whichmeans that } \frac{V_d}{V_c}=\frac{V_a}{V_b}.$

Comparing the expression for thermal efficiencyEq. (3.4) with Eq. (3.5) arată două consecințe. În primul rând, încălzirile primite și respinse sunt legate de temperaturile părților izoterme ale ciclului de

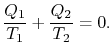$\displaystyle \frac{Q_1}{T_1}+\frac{Q_2}{T_2}= 0.$

(3..6)

în al doilea rând, eficiența unui ciclu Carnot este dată compact de

$\displaystyle \eta = 1 - \frac{T_1}{t_2}.\qquad \ textbf {eficiența ciclului Carnot.}$

(3..7)

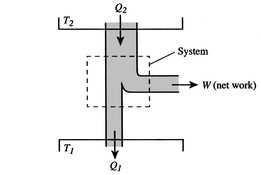
eficiența poate fi de 100% numai dacă temperatura la care este respinsă căldura este zero. Transferurile de căldură și de lucru către și dinspre sistem sunt prezentate schematic în figura 3.5.

figura 3.5:De lucru și transferuri de căldură Ina ciclu Carnot între două rezervoare de căldură

ă>

puncte noroioase

Din $\eta = 1- {T_1}/{T_2}$ , uita la grafic, doeaceasta înseamnă mai departe în afară izoterme sunt mai eficiente? Și dacă ar fi foarte apropiați, ar fifoarte ineficient? (MP 3.2)