expertiză: intermediar
Ce este o funcție spline?
trebuie să știm care sunt caracteristicile esențiale ale splinelor înainte de a ne gândi cum să construim un sistem de bază pentru ele.
funcțiile Spline sunt formate prin unirea polinoamelor împreună la puncte fixenumite noduri. Adică împărțim intervalul care se extinde de la limita inferioară tllimita superioară tU peste care dorim să aproximăm o curbă în L + 1 sub-intervalsseparat de l limitele interioare numite noduri, sau uneori puncte de întrerupere.) Există o distincție între acești doi termeni, dar vom ajunge la acest lucru mai târziu.luați în considerare cel mai simplu caz în care un singur punct de întrerupere împarte intervalul în două subintervale. Splinefuncția este, în fiecare interval, un polinom de grad specificat(cea mai mare putere care definește polinomul) sau ordine (numărul de coeficienți care definesc polinomul, care este încă unuldecât gradul său). Să folosim m pentru a desemna ordinea polinomului, astfel încâtgradul este m-1:
la punctul de întrerupere interior, cele două polinoame trebuie să se unească fără probleme. În cel mai frecvent caz, aceasta înseamnă că derivatele se potrivesc cu ordinul cu unul mai mic decât gradul. De fapt, dacă s-ar potrivi cu derivata a cărei ordine ar egala gradul, ar fi același polinom. Astfel, o funcție spline definită în acest was are un grad suplimentar de libertate decât un polinom care se extinde pe întregul interval.
De exemplu, fiecare polinom să fie un segment de linie dreaptă și, prin urmare, de gradul unu. În acest sens, se alătură la punctul de întrerupere cu derivative potrivitepână la gradul 0; pe scurt, se alătură pur și simplu și au valori identice la punctul de întrerupere. Deoarece primul polinom are două grade de libertate (pantă și interceptare), iar al doilea, având valoarea deja definită la punctul de rupere,este lăsat cu un singur grad de libertate (pantă), linia poligonală totală are treigrade de libertate.
în mod corespunzător ,dacă ambele polinoame sunt quadratice, atunci se potrivesc atât în termeni de valori, cât și în termeni de pantă a primului derivativla ecu1. Primul polinom are trei grade de libertate, dar al doilea pierde două, deoarece dacăconstrângerea asupra valorii și pantei sale la oquti, și astfel păstrează doar unul. Acest lucru lasă un total de patru grade de libertate pentru splinefunctionformed în acest fel, asopus la trei pentru un polinom pătratic pe întregul interval. Figura 1 prezintă acesteacazuri liniare și patratice cu un singur punct de întrerupere.
care sunt câteva exemple de funcții de bază utilizate în mod obișnuit?
acum putem generaliza situația la L puncte de întrerupere interioare, șio funcție spline fiind de ordinul m sau gradul m-1 pe fiecare sub-interval. Primul segment polinomial are o completare completă a gradelor m de libertate, dar fiecare segment ulterior are doar un grad de libertate din cauza constrângerilor m – 1 asupra comportamentului său.Acest lucru oferă un total de l + m grade de libertate, sau numărul depuncte interioare plus ordinea segmentelor polinomiale.
astfel, funcțiile spline sunt în esență generalizări ale noțiunii de poligonaline. Își câștigă flexibilitatea în două moduri: în primul rând, prin ordineapolinomii din care sunt construite și, în al doilea rând, prin numărul de puncte de spargereutilizate. De obicei, alegem să menținem ordinea fixă și să adăugăm puncte de întrerupere necesare pentru a obține flexibilitatea necesară.
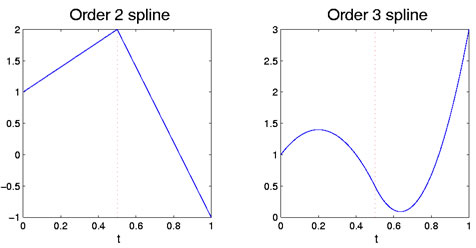
Figura 1: figura din stânga prezintă o funcție spline de ordinul doi, care este liniară în bucăți. Cifra corectă este o linie de comandă 3, careeste pătratică în bucăți. Punctul de pauză la 0,5 este indicat de linia punctată verticală roșie.