Distribuții normale( curba clopotului): definiție, probleme de cuvinte

Probabilitate și statistici > distribuții normale

cuprins:

1. ce este o distribuție normală?
2. modelul Normal standard
3. probleme normale cuvânt de distribuție.
4. distribuție normală pe TI 89 Exemple
5. articole conexe.

ce este o distribuție normală?

o distribuție normală.

o distribuție normală, uneori numită curba clopotului, este o distribuție care apare în mod natural în multe situații. De exemplu, curba clopotului este văzută în teste precum SAT și GRE. Cea mai mare parte a studenților va înscrie media (C), în timp ce un număr mai mic de studenți va înscrie un B sau D. Un procent și mai mic de studenți va înscrie un F sau un A. aceasta creează o distribuție care seamănă cu un clopot (de unde și porecla). Curba clopotului este simetrică. Jumătate din date vor cădea la stânga mediei; jumătate va cădea la dreapta.
multe grupuri urmează acest tip de model. De aceea este utilizat pe scară largă în afaceri, statistici și în organisme guvernamentale precum FDA:

• înălțimile oamenilor.
• erori de măsurare.
• tensiunea arterială.
• puncte pe un test.
• scoruri IQ.
• salarii.

regula empirică vă spune ce procent din datele dvs. se încadrează într-un anumit număr de abateri standard de la medie:
• 68% Din date se încadrează într-o abatere standard a mediei.• 95% din date se încadrează în două abateri standard ale mediei.• 99,7% din date se încadrează în trei abateri standard ale mediei.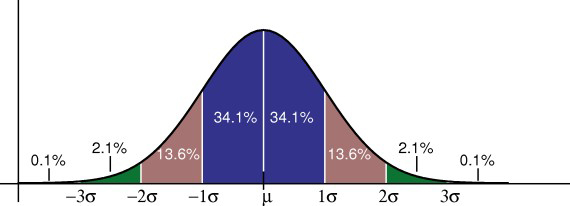

deviația standard controlează răspândirea distribuției. O abatere standard mai mică indică faptul că datele sunt strâns grupate în jurul mediei; distribuția normală va fi mai înaltă. O abatere standard mai mare indică faptul că datele sunt răspândite în jurul mediei; distribuția normală va fi mai plată și mai largă.

proprietățile unei distribuții normale

• media, modul și mediana sunt toate egale.
• curba este simetrică în centru (adică în jurul mediei, INQ).
• exact jumătate din valori sunt la stânga centrului și exact jumătate din valori sunt la dreapta.
• suprafața totală de sub curbă este 1.

modelul Normal Standard
un model normal standard este o distribuție normală cu o medie de 0 și o abatere standard de 1.

Modelul Standard Normal: Distribuția datelor

o modalitate de a afla cum sunt distribuite datele este de a le trasa într-un grafic. Dacă datele sunt distribuite uniform, puteți veni cu o curbă de clopot. O curbă clopot are un procent mic de puncte pe ambele cozi și procentul mai mare pe partea interioară a curbei. În modelul normal standard, aproximativ 5 la sută din datele dvs. ar cădea în „cozi” (portocaliu mai închis în imaginea de mai jos) și 90 la sută vor fi între ele. De exemplu, pentru scorurile de testare ale studenților, distribuția normală ar arăta 2,5% dintre studenți obținând scoruri foarte mici și 2.5 la sută obținând scoruri foarte mari. Restul va fi la mijloc; nu prea mare sau prea mic. Forma distribuției normale standard arată astfel:

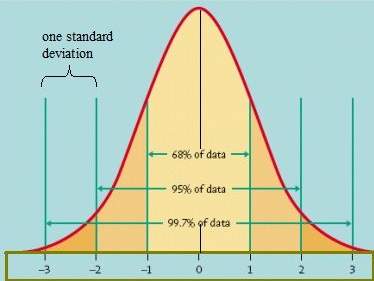
model normal standard. Credit imagine: Universitatea din Virginia.

aplicații practice ale modelului Normal Standard

distribuția normală standard vă poate ajuta să vă dați seama la ce subiect obțineți note bune și la ce subiecte trebuie să depuneți mai mult efort datorită procentelor scăzute de punctaj. Odată ce obțineți un scor într-un subiect care este mai mare decât scorul dvs. într-un alt subiect, ați putea crede că sunteți mai bine în subiectul în care ați obținut scorul mai mare. Acest lucru nu este întotdeauna adevărat.

puteți spune că sunteți mai bine într-un anumit subiect dacă obțineți un scor cu un anumit număr de abateri standard peste medie. Abaterea standard vă spune cât de strâns sunt grupate datele dvs. în jurul mediei; vă permite să comparați diferite distribuții care au diferite tipuri de date — inclusiv mijloace diferite.

de exemplu, dacă obțineți un scor de 90 la matematică și 95 în Engleză, ați putea crede că sunteți mai bun în engleză decât în matematică. Cu toate acestea, în matematică, scorul dvs. este de 2 abateri standard peste medie. În limba engleză, este doar o abatere standard peste medie. Vă spune că în matematică, scorul dvs. este mult mai mare decât majoritatea studenților (scorul dvs. cade în coadă).
pe baza acestor date, te-ai descurcat mai bine la matematică decât la engleză!

întrebările de probabilitate folosind modelul Standard

întrebările despre probabilitatea standard de distribuție normală pot părea alarmante, dar cheia rezolvării lor este înțelegerea a ceea ce reprezintă aria de sub o curbă normală standard. Suprafața totală sub o curbă de distribuție normală standard este de 100% (adică „1” ca zecimală). De exemplu, jumătatea stângă a curbei este de 50% sau .5. Deci probabilitatea ca o variabilă aleatorie să apară în jumătatea stângă a curbei este .5. desigur, nu toate problemele sunt chiar atât de simple, de aceea există un tabel Z. Tot ce face un tabel z este să măsoare acele probabilități (adică 50%) și să le plaseze în abateri standard de la medie. Media este în centrul distribuției normale standard și o probabilitate de 50% este egală cu zero abateri standard.

distribuție normală Standard: cum să găsiți probabilitatea (pașii)

Pasul 1: Desenați o curbă de clopot și o umbră în zona solicitată în întrebare. Exemplul de mai jos arată z >-0.8. Asta înseamnă că căutați probabilitatea ca z să fie mai mare de -0,8, deci trebuie să trasați o linie verticală la -0.8 abateri standard de la medie și umbră tot ceea ce este mai mare decât acest număr.

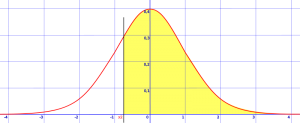
zona umbrită este z> -0.8

Pasul 2: Vizitați indexul normal al zonei de probabilitate și găsiți o imagine care arată ca graficul dvs. Urmați instrucțiunile de pe acea pagină pentru a găsi valoarea z pentru Grafic. Valoarea z este probabilitatea.

sfat: Pasul 1 este opțional din punct de vedere tehnic, dar este întotdeauna o idee bună să schițați un grafic atunci când încercați să răspundeți la probleme de probabilitate. Asta pentru că majoritatea greșelilor se întâmplă nu pentru că nu poți face matematica sau citi un tabel z, ci pentru că scazi un scor z în loc să adaugi (adică îți imaginezi probabilitatea sub curbă în direcția greșită. O schiță vă ajută să vă cimentați în cap exact ceea ce căutați.

dacă încă mai aveți probleme, consultați tutorii de la Chegg.com. primele 30 de minute cu un tutore live sunt gratuite!

probleme normale de distribuție a cuvintelor

acest videoclip prezintă un exemplu de problemă normală a cuvintelor de distribuție. Pentru mai multe exemple, citiți mai jos:

când abordați distribuția normală într-o clasă de statistici, încercați să găsiți zona de sub curbă. Suprafața totală este de 100% (ca zecimală, adică 1). Problemele normale de distribuție vin în șase tipuri de bază. De unde știi că o problemă de cuvânt implică o distribuție normală? Căutați expresia cheie” presupuneți că variabila este distribuită în mod normal „sau” presupuneți că variabila este aproximativ normală.”Pentru a rezolva o problemă de cuvânt, trebuie să vă dați seama ce tip aveți.

1. „între”: Conține expresia „între” și include o limită superioară și o limită inferioară (adică „găsiți numărul de case la prețuri cuprinse între $50k și 200k”).
2. „mai mult decât” sau „deasupra”: conține expresia” mai mult decât „sau”deasupra”.
3. „mai puțin de”.
4. Lower Cut Off exemplu (video)
5. Upper Cut Off exemplu (video)
6. Middle percent exemplu (video)

„între”

Acest mod de a acoperi rezolvarea problemelor care conțin expresia „între” și include o limită superioară și inferioară (adică „găsiți numărul de case la prețuri cuprinse între $50k și 200k”. Rețineți că acest lucru este diferit de găsirea „procentului mediu” al ceva.

probleme de cuvinte cu distribuție normală: „între”: pași

Pasul 1: identificați părțile problemei cuvântului. Cuvântul problemă va identifica:

1. media (medie sau INQ).
2. deviația Standard (XV).
3. numărul selectat (adică „alegeți unul la întâmplare” sau „selectați zece la întâmplare”).
4. X: numerele asociate cu „între” (adică „între 5.000 și 10.000 USD” ar avea X ca 5.000 și ca 10.000 USD).

în plus, vi se va da fie:

1. dimensiunea eșantionului (adică 400 de case, 33 de persoane, 99 de fabrici, 378 de instalatori etc.). Sau
2. s-ar putea să vi se solicite o probabilitate (caz în care dimensiunea eșantionului dvs. va fi cel mai probabil toată lumea, adică „instalatori călători” sau „piloți din primul an.”

Pasul 2: Desenați un grafic. Puneți media pe care ați identificat-o la Pasul 1 în centru. Puneți numărul asociat cu „Între” pe grafic (ghiciți unde ar cădea numerele–nu trebuie să fie exact). De exemplu, dacă media dvs. a fost de 100 USD și vi s-a cerut „salarii orare între 75 și 125 USD”) graficul dvs. va arăta cam așa:

Pasul 3: Aflați scorurile z. Conectați prima valoare X (în graficul meu de mai sus, este 75) în formula valorii z și rezolvați. Valoarea de 100 din graficul eșantionului. Puteți obține aceste cifre (inclusiv în funcție de cifra de afaceri, deviația standard) din răspunsurile dvs. la Pasul 1 :

*Notă: Dacă formula vă confundă, tot ce vă cere această formulă este:
1. scădeți media din X
2. împărțiți la deviația standard.

Pasul 4: Repetați pasul 3 pentru al doilea X.

Pasul 5: Luați numerele de la Pasul 3 și 4 și folosiți-le pentru a găsi zona din tabelul Z.

dacă vi s-a cerut să găsiți o probabilitate în întrebarea dvs., mergeți la Pasul 6a. dacă vi s-a cerut să găsiți un număr dintr-o anumită dimensiune a eșantionului, mergeți la Pasul 6b.

pasul 6a:

convertiți răspunsul de la Pasul 5 într-un procent.

de exemplu, 0,1293 este 12,93%.

asta este–săriți pasul 6b!

pasul 6b

înmulțiți dimensiunea eșantionului (găsită la Pasul 1) cu valoarea z pe care ați găsit-o la Pasul 4. De exemplu, 0,300 * 100 = 30.

asta e!

„mai mult decât” sau „mai sus”

acest mod de rezolvare a problemelor normale de distribuție care conțin expresia „mai mult decât” (sau o frază de genul „mai sus”).

Pasul 1: împărțiți cuvântul problemă în părți. Găsi:

1. media (medie sau INQ)
2. deviația Standard (INQ)
3. un număr (de exemplu, „alegeți cincizeci la întâmplare” sau „selectați 90 la întâmplare”)
4. X: numărul asociat cu declarația „mai puțin de”. De exemplu, dacă vi s-a cerut să găsiți „sub 9.999 USD”, atunci X este 9.999.

Pasul 2: Găsiți eșantionul din problemă. Veți avea fie o dimensiune specifică (cum ar fi „1000 de televizoare”), fie un eșantion general („fiecare televizor”).

desenați o imagine dacă problema cu media și zona pe care o căutați. De exemplu, dacă Media este de 15 USD și vi s-a cerut să aflați ce mese costă mai mult de 10 USD, graficul dvs. ar putea arăta astfel:

Pasul 3: Calculați scorul z (conectați valorile la Z valoare formula și rezolva). Utilizați răspunsurile de la Pasul 1 :

practic, tot ce faceți cu formula este scăderea mediei din X și apoi împărțirea răspunsului la deviația standard.

Pasul 4: Găsiți zona folosind scorul z de la Pasul 3. Utilizați tabelul Z. Nu sunteți sigur cum să citiți un tabel z? Vedeți videoclipul de pe pagina Z-table.

Pasul 6: mergeți la Pasul 6a pentru a găsi o probabilitate sau mergeți la Pasul 6b pentru a calcula un anumit număr sau sumă.

pasul 6a
transformați răspunsul pasului 5 într-un procent.

de exemplu, 0,1293 este 12,93%.

săriți pasul 6b: ați terminat!

pasul 6b
înmulțiți dimensiunea eșantionului de la Pasul 1 cu scorul z de la Pasul 4. De exemplu, 0,500 * 100 = 50.

ai terminat!

Less Than

acest mod de abordare acoperă rezolvarea problemelor normale ale cuvintelor de distribuție care au expresia „less than” (sau o expresie similară, cum ar fi „less than”).

probleme normale de distribuție a cuvintelor mai mici decât: pași

Pasul 1: împărțiți problema cuvântului în părți:

1. media (medie sau INQ)
2. deviația Standard (INQ)
3. numărul selectat (adică. „alegeți unul la întâmplare” sau „selectați zece la întâmplare”)
4. X: numărul care merge cu” mai puțin de „(adică” sub 99.000 USD ” ar Lista X ca 99.000)

în plus, veți avea fie:

1. o dimensiune specifică a eșantionului. De exemplu, 500 de bărci, 250 de sandvișuri, 100 de televizoare etc.
2. toată lumea din eșantion (vi se va cere să găsiți o probabilitate). De exemplu, „studenții la medicină din primul an”,” pacienții cu Cancer „sau” piloții companiilor aeriene.”

Pasul 2: Desenați o imagine pentru a vă ajuta să vizualizați problema. Următorul grafic arată o medie de 15 și o zonă „sub 4”):

Pasul 3: găsiți valoarea z conectând valorile date în formulă. „X” din graficul nostru de probă este 4, iar cel de-al doilea (sau media) este 15. Puteți obține aceste cifre (inclusiv în cazul în care deviația standard) de la răspunsurile la Pasul 1, în cazul în care ați identificat părțile problemei:

tot ce trebuie să faceți pentru a rezolva formula este:

1. scade media din X.
2. împărțiți la deviația standard.

Pasul 4: luați numărul de la Pasul 3, apoi utilizați tabelul z pentru a găsi zona.

Pasul 5:pentru a găsi o probabilitate, mergeți la Pasul 6a. pentru a găsi un număr dintr-o anumită dimensiune a eșantionului, mergeți la Pasul 6b.

pasul 6a

schimbați numărul de la Pasul 5 în procent.

de exemplu, 0,1293 este 12,93%.

asta e!

pasul 6b

înmulțiți dimensiunea eșantionului (găsită la Pasul 1) cu valoarea z pe care ați găsit-o la Pasul 4. De exemplu, 0,300 * 100 = 30.

asta e!

Lower Cut off

uneori, pe o problemă de distribuție normală cuvânt vi se va cere să găsească o „limită inferioară a unui procent superior” de ceva (de exemplu, „găsi punctul de cut-off pentru a trece un anumit examen în cazul în care partea de sus 40% din factorii de testare trece”). Un punct de tăiere mai mic este punctul în care scorurile vor scădea sub acel punct. De exemplu, s-ar putea să doriți să găsiți unde este punctul de tăiere pentru 10% din cei care efectuează teste.

vă rugăm să acceptați Statistici, Cookie-uri de marketing pentru a viziona acest videoclip.

consultați canalul nostru YouTube pentru mai multe probleme lucrate.

distribuție normală TI 89 Exemple

în Statisticile elementare, veți fi adesea confruntat cu o întrebare care vă cere punctele tăiate pentru un anumit procent din distribuția normală, cum ar fi primele 90% sau primele 10%. În timp ce elaborarea acestor tipuri de probleme de mână este greoaie, TI-89 calculator grafic face munca lumina de a găsi tăiat puncte pentru un procent de top cu funcția normală inversă. Ceea ce faci de fapt este în căutarea pentru tăiat puncte pentru o anumită percentila: de exemplu, dacă aveți o listă de note și doriți să știți ce scor este la percentila 99, puteți utiliza funcția normală inversă pentru a găsi acel punct de întrerupere procentual.

găsirea tăiat puncte pentru un procent de Top

problema eșantion: elevii de la un anumit colegiu medie 5 picioare 8 inch (68 inch) inaltime. Înălțimile sunt distribuite în mod normal, cu o abatere standard de 2,5 inci. Care este valoarea care separă primele 1% din înălțimi de restul populației?

Pasul 1: Apăsați aplicații și utilizați tastele de defilare pentru a evidenția statistici / listă Editor.

Pasul 2: Apăsați F5 2 1 (Aceasta vă duce la ecranul Normal invers).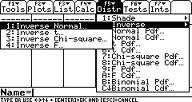

Pasul 3: Introduceți 0,99 în caseta zonă.

Pasul 4: Introduceți 68 în caseta de la numărul de telefon.

Pasul 5: Introduceți 2.5 în caseta de la numărul de telefon.

Pasul 6: apăsați ENTER.

Pasul 7: citiți rezultatele: invers=73.8159 înseamnă că înălțimea tăiată pentru percentila 99 este de 73.8159 inci.

asta e!

exemplu de proporție de probabilitate (funcția NormalCDF)

exemplu de întrebare: Un grup de studenți cu salarii distribuite în mod normal câștigă în medie 6.800 USD cu o abatere standard de 2.500 USD. Ce proporție de studenți câștigă între $6,500 și $7,300?

Pasul 1: Apăsați aplicații. Derulați până la editorul statistici/listă și apăsați ENTER.

Pasul 2: apăsați F5 4.

Pasul 3: Introduceți 6500 în caseta valoare inferioară.

Pasul 4: Introduceți 7300 în caseta valoare superioară.

Pasul 5: Introduceți 6800 în caseta de la numărul de telefon.

Pasul 6: Introduceți 2500 în caseta de la articolul de referință. Apăsați ENTER.

Pasul 7: citiți răspunsul. Cdf=.127018. Cu alte cuvinte,.013, sau 13% dintre studenți câștigă între 6.500 și 7.300 USD.

TI-89 graficarea unei curbe normale de distribuție

TI-89 nu poate calcula doar scorurile z și valorile de returnare pentru distribuțiile normale, ci poate și graficul curbei normale de distribuție. Graficarea unei distribuții normale vă poate ajuta să vedeți ce ar trebui să căutați și vă oferă încă un instrument în rezolvarea problemelor normale de distribuție. TI – 89 poate Grafic o curbă de distribuție normală cu o zonă umbrită pentru orice valoare. De exemplu, puteți crea un grafic care este: mai mic decât un anumit număr, mai mare decât un anumit număr sau între un anumit set de numere.

exemplu de problemă: desenați o curbă de distribuție normală pentru salariile studenților în timpul unui semestru tipic. Salariile studenților au o medie de $6,800 și deviația standard de $2,500. Umbriți zona de pe grafic care corespunde salariilor între 7.300 și 9.000 USD.

Pasul 1: Apăsați aplicații și selectați editorul statistici / listă.

Pasul 2: apăsați F2 3 și F2 4.

Pasul 3: Apăsați F5) 1.

Pasul 4: Derulați în jos și introduceți 7300 în caseta valoare inferioară.

Pasul 5: Derulați în jos și introduceți 9000 în caseta valoare superioară.

Pasul 6: defilați în jos și introduceți 6800 în caseta de la numărul de telefon.

Pasul 7: defilați în jos și introduceți 2500 în caseta de la numărul de telefon.

Pasul 8: Derulați în jos. Rotiți Scala automată la ” Da ” apăsând tasta de parcurgere din dreapta, apoi tasta de parcurgere în jos pentru a selecta Da. Apăsați ENTER.

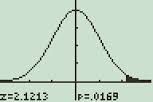
un grafic de distribuție normală afișat pe calculatorul TI-89.

asta e!

Tip: Dacă doriți să introduceți ca una dintre valorile dvs. inferioare sau superioare, apăsați tasta diamond și apoi Catalog.

Beyer, W. H. CRC tabele matematice standard, ediția a 28-a. Boca Raton, FL: CRC Press, pp. 533-534, 1987.Feller, W. O Introducere în teoria probabilităților și aplicațiile sale, Vol. 1, 3 ed. New York: Wiley, 1968.
Kenney, J. F. și păstrarea, E. S. matematica statisticii, pt. 2, Ediția a 2-a. Princeton, NJ: Van Nostrand, 1951.
Kraitchik, M. ” curba de eroare.”6.4 în recreații matematice. New York: W. W. Norton, PP. 121-123, 1942.Patel, J. K. și Read, C. B. Manualul distribuției normale. New York: Dekker, 1982.

1. care este regula 68-95-99.7?
2. caseta de transformare Cox
3. caseta Muller transforma
4. modele amestec Gaussian.
5. ce este un complot probabilitate normală?
6. cum se calculează un scor Z în statistici
7. găsiți zona din dreapta unui scor Z.
8. folosind aproximarea normală pentru a rezolva o problemă binomială
9. care este factorul de corecție a continuității?
10. zona sub un indice normal al curbei de distribuție
11. teorema limitei centrale.
12. distribuția normală oblică.
13. curba normală cu două cozi.
14. funcția Q.

citați acest lucru ca:
Stephanie Glen. „Distribuții normale (curba clopotului): definiție, probleme de cuvinte” din StatisticsHowTo.com: statistici elementare pentru restul dintre noi! https://www.statisticshowto.com/probability-and-statistics/normal-distributions/

——————————————————————————

aveți nevoie de ajutor cu o temă sau o întrebare de testare? Cu studiul Chegg, puteți obține soluții pas cu pas la întrebările dvs. de la un expert în domeniu. Primele 30 de minute cu un tutore Chegg sunt gratuite!