Parsimonie maximă pe rețelele filogenetice

definiția rețelelor filogenetice

urmăm definiția rețelelor filogenetice așa cum este dată în definiția 4 , Pagina 16]. Pentru toate celelalte definiții grafice-teoretice care nu sunt date aici, urmăm . O rețea filogenetică înrădăcinată, numită pur și simplu aici o rețea filogenetică, este definită ca un graf aciclic înrădăcinat, direcționat (DAG), a cărui rădăcină are gradul 0 și frunzele au gradul 0. Vârfurile a căror grad este mai mare de 1 se numesc vârfuri reticulate, iar marginile cu vârfuri reticulate ca vârfuri de cap se numesc margini reticulate. Toate celelalte margini sunt denumite margini de copac. Definiția dată în are grijă de așa-numita reținere a „consistenței timpului”, și anume că marginile arborelui au loc într-un timp pozitiv, iar vârfurile reticulate au părinți care pot „coexista doar în timp”. Prin urmare, înainte, ne amintim definiția formală a rețelelor filogenetice așa cum este dată în .

având în vedere orice grafic direcționat, spunem că două vârfuri u și v nu pot coexista în timp dacă există o secvență P = (p1, p2,…, p k ) de căi în N astfel încât:

1. p i este o cale direcționată care conține cel puțin o muchie de copac, pentru fiecare 1 ixtxtck,

2. u este coada lui p 1 , iar v este capul lui PK, și

3. pentru fiecare 1 ixtctck – 1, există un nod de rețea ai cărui doi părinți sunt Capul p i și coada lui p i+1.

o rețea filogenetică N este un DAG înrădăcinat care respectă următoarele constrângeri:

1. fiecare nod are un grad și un grad mai mare definite de una dintre cele patru combinații (0, 2), (1, 0), (1, 2), sau (2, 1) – corespunzând, respectiv, rădăcinii, frunzelor, vârfurilor interne ale arborelui și vârfurilor reticulate. Toate vârfurile, altele decât vârfurile reticulate, se numesc vârfuri de copac.

2. Dacă două noduri u și v nu pot coexista în timp, atunci nu există un nod de rețea w cu muchii (u, w) și (v, w).

3. având în vedere orice margine a rețelei, cel puțin unul dintre punctele sale finale trebuie să fie un nod arbore.

O altă componentă a acestei definiții este că pentru orice margine din rețeaua filogenetică, cel puțin unul dintre punctele sale finale (fie capul, fie coada) este un vârf de copac. Aici, vom folosi această definiție. Ori de câte ori este posibil, subliniem dacă sunt necesare condițiile definiției.

rețelele filogenetice pot fi gândite ca o rețea care conține subgrafuri, copacii care explică istoriile evolutive ale diferitelor segmente ale secvențelor terminale de intrare. Având în vedere o rețea filogenetică, ștergerea unuia din fiecare incident de margine la un vârf reticulat nu garantează un arbore filogenetic rezultat cu același set de frunze ca cel al rețelei. Aceasta este o proprietate nedorită, mai ales dacă criteriul parsimoniei este definit prin găsirea unui arbore filogenetic în interiorul rețelei care este cel mai parsimonios pentru site-ul dat, așa cum este definit în . Pentru a evita această problemă, este necesar să presupunem că nici un vârf intern nu are doi copii reticulați. Numim această clasă de rețele filogenetice ca o rețea filogenetică fără reticulări surori. Vezi Figura 1 pentru câteva exemple de rețele filogenetice.

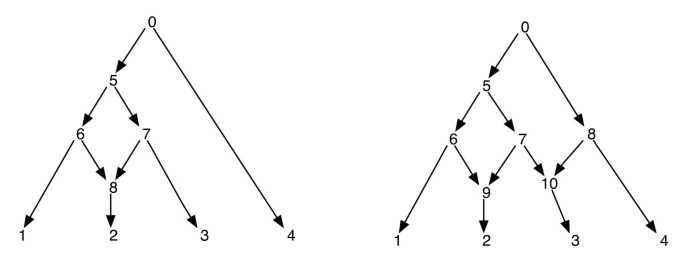
rețele filogenetice. Figura prezintă două rețele filogenetice; cea din stânga are doar un singur vârf reticulat, iar cea din dreapta are două vârfuri reticulate care sunt surori între ele. Rețineți că eliminarea marginilor (7, 9) și (7, 10) din rețeaua din dreapta nu are ca rezultat un copac în care vertex 7 este o frunză. Acest lucru arată că eliminarea unei muchii de intrare fiecare pe vertex reticulat nu produce neapărat un copac cu același set de frunze ca rețeaua. Post-ordonarea și precomanda nodurilor rețelei din stânga sunt 1, 2, 8, 6, 3, 7, 5, 4, 0 și 0, 5, 6, 1, 8, 2, 7, 3, 4 respectiv și pentru rețeaua din dreapta, acestea sunt 1, 2, 9, 6, 3, 10, 7, 5, 4, 8, 0 și 0, 5, 6, 1, 9, 2, 7, 10, 3, 8, 4 respectiv.

înainte de a trece la definirea problemelor parsimonie, ceea ce urmează este o observație utilă. Pentru o rețea filogenetică N fără reticulații surori și având r vârfuri reticulate și cu setul de frunze X, notăm T ( N ) ca mulțimea tuturor copacilor conținuți în N. fiecare astfel de copac este obținut urmând doi pași: (1) pentru fiecare vârf reticulat, îndepărtați una dintre marginile primite și apoi (2) pentru fiecare vârf v de grad și grad 1, al cărui părinte este u și copil este w, contractați marginile (u, v) și (v, w) într-o singură margine (u, w). Condiția ca fiecare margine din N să aibă un vârf de copac ca punct final și ca fiecare vârf de copac să aibă cel puțin un vârf de copac ca un copil, asigură că setul de frunze ale arborelui rezultat este același cu cel al rețelei. Prin urmare, setul T ( N ) conține exact 2rphylogenetic copaci al căror set de frunze este exact X.

Parsimonie maximă

ne referim la cititori pentru o descriere generală a ideii de parsimonie și la discutarea diferiților algoritmi de parsimonie. S-a subliniat că metoda de parsimonie pentru copaci poate fi extinsă la rețelele filogenetice. Într-o serie de lucrări , un astfel de criteriu de parsimonie este definit prin găsirea unui copac în rețea care are cel mai bun scor parsimonios și au fost concepuți algoritmi eficienți pentru optimizarea acestui criteriu pe o rețea filogenetică dată. Deși se arată că acești algoritmi funcționează bine în practică, ei pot funcționa corect numai pentru rețelele filogenetice fără reticulări surori, deoarece este simplu să căutați un arbore optim în aceste clase restrânse de rețele. În această secțiune, prezentăm o versiune alternativă a problemei parsimoniei și în secțiunile următoare oferim câteva soluții euristice pentru optimizarea scorului pe orice rețea filogenetică.

fie = {1, 2, …, n} denumiți setul de etichete de frunze ale unei rețele filogenetice date N. o funcție sec: sec {0, 1, …,|Σ| – 1} se numește un stat misiune funcția de peste alfabetul Σ (un non-vidă) pentru N. spunem că o funcție λ ^ :V ( N ) → { 0 , 1 , … , | Σ | – 1 } este o extensie a λ N, și dacă este de acord cu λ pe frunze de N. Pentru un vertex v în N, numim XV ^ (v ) ca o atribuire a lui XV ^ pe v. o rețea complet atribuită este o rețea în care toate vârfurile au etichete de la {0, 1, …, |Σ| – 1}. Fie C o matrice de cost a cărei ijth intrare c ij este costul transformării de la starea i la starea j de-a lungul oricărei margini din N. Dacă e = (u, v) este o margine în N, unde u este părintele lui v, denotăm w e ( ecuot ) ^ = c I j , unde i= ecuot ^ ( u ) și j= ecuot ^ ( v ) . Pentru un grafic G, lăsăm E (G) să desemneze setul de margini al lui G. apoi problema parsimoniei este definită după cum urmează.

intrare: Un filogenetic rețea N cu frunze de etichete și o stare de atribuire funcția λ peste alfabetul Σ pentru N.

Parcimonie criteriu: Pentru o extensie λ ^ de λ, să

și

ieșire: având în vedere P} {P1, P2}, găsiți ^ care minimizează p ( ^ ).

remarcăm că P 1 ( XV ^ ) este introdus în și P 2 ( XV ^ ) este definiția pe care o vom folosi în această lucrare. O abordare mai generală este aceea de a minimiza Q ( XV^) = XV e e ( n ) d e ( w e ( XV ^ ) ) , unde d e este o funcție de greutate non-negativă pe marginile N. În sensul acestei lucrări, ne limităm la P = P2, deși prima dintre abordările noastre, soluția de programare dinamică este valabilă și pentru p = Q.

algoritmi de Parsimonie pe rețele

traversând o rețea filogenetică

traversal se referă la procesul de vizitare a fiecărui vârf, exact o dată, într-un mod sistematic. Astfel de traversări sunt clasificate după ordinea în care sunt vizitate vârfurile. Avem nevoie de două tipuri de traversări de noduri de rețea pentru a descrie algoritmii noștri. Acestea sunt bine cunoscute pentru arborii filogenetici și le prezentăm aici pentru rețelele filogenetice. Algoritmii pentru traversările date mai jos pornesc de la orice vârf v dat în rețea. În această lucrare, vom efectua întotdeauna traversările de la vârful rădăcină al rețelei.

traversare precomandă a unei rețele filogenetice de la un vârf v

1. vizitați vârful v.

2. efectuați recursiv traversarea precomandă de la fiecare copil care nu a fost încă vizitat.

traversarea Post-comandă a unei rețele filogenetice dintr-un nod v

1. efectuați recursiv traversarea post-comandă de la fiecare copil care nu a fost încă vizitat.

2. vizitați vertexul v.

deoarece o rețea filogenetică este un DAG, astfel de traversări vor vizita toate vârfurile rețelei exact o dată. (Consultați pentru mai multe detalii despre existența pe astfel de traversări pe DAGs). În sensul acestei lucrări, presupunem că vârfurile unei rețele sunt etichetate în mod unic de numere întregi. Rețineți că frunzele sunt deja etichetate din set ; și astfel folosim alte numere întregi pentru alte vârfuri. Ori de câte ori vârfurile copil ale v sunt extrase, ele sunt, de asemenea, aranjate în ordinea crescătoare a etichetelor lor întregi, iar traversările pre – și post-order sunt efectuate în această ordine. Acest lucru va asigura următoarele: dacă vârfurile v și v ‘sunt astfel încât nu există o cale direcționată între ele, atunci vertexul v este traversat înainte de vertexul v’ în Precomandă dacă și numai dacă vertexul v este traversat înainte de vertexul v’ în post-ordine. Vezi Figura 1 pentru câteva exemple. Cu această proprietate, observăm că traversele pre – și post-comandă de la rădăcina unei rețele filogenetice urmăresc fiecare același arbore întins, pe care îl numim aici arborele transversal.

soluție de programare dinamică

programarea dinamică este utilizată pentru a oferi soluții eficiente pentru găsirea scorului exact de parsimonie atunci când rețeaua este un arbore filogenetic . În această secțiune, arătăm că aceeași abordare poate fi generalizată la rețelele filogenetice. Algoritmul lui Sankoff pe un copac traversează vârfurile arborelui prin post-comandă în timp ce calculează costurile minime ale fiecărei stări la fiecare vârf de la frunze la rădăcină și apoi alege cele mai bune sarcini pe fiecare vârf prin backtracking de la rădăcină la frunze prin traversarea vârfurilor arborelui prin precomandă. Ambele faze sunt prezentate pentru rețele în algoritmii 1 și respectiv 2. Le descriem pe scurt mai jos. Se poate observa că, dacă rețeaua este un copac, atunci algoritmii noștri se potrivesc cu fazele de precomandă și post-comandă ale metodei Sankoff pentru copaci.

având în vedere o rețea filogenetică N, cu vârfuri de frunze etichetate și cu funcție de atribuire a stării de peste alfabet de la sută, se atribuie fiecărui vârf v de la sută v o cantitate S v (i) pentru fiecare i de la sută. În arborii filogenetici, S v (i) denotă suma minimă a costurilor tuturor evenimentelor de la vârful v la toate frunzele care pot fi accesate de la v, având în vedere că lui v i se atribuie starea i și tuturor vârfurilor descendente din v li se atribuie fiecare o stare. În rețele, nu există o modalitate simplă de a calcula o astfel de cantitate. În schimb, permitem S v (i) să fie o limită inferioară a scorului exact de mai sus și se calculează în timpul fazei de traversare post-comandă.

faza de traversare Post-comandă: dacă v este o frunză de N, atunci S v (i) este atribuit 0 dacă starea observată este starea i și infinit altfel. Acum tot ce avem nevoie este o relație de recursivitate pentru a calcula S v (i) pentru restul vârfurilor. Pentru fiecare copil w din v, spunem că w satisface condiția de traversare post-Comandă cu privire la v sau pur și simplu condiția de traversare cu privire la v, având în vedere observația de la începutul acestei secțiuni, dacă următoarele dețin:

1. (i)

   vertexul w este un vertex reticulat și

2. (ii)

   dacă v’ este părintele lui w altul decât v, atunci vertexul v trebuie traversat înainte de v’ în traversala post-comandă a lui N.

acum definim recursiv pentru fiecare margine (v, w),

pentru un arbore filogenetic, s(v, w)(i) presupune întotdeauna prima dintre aceste cantități și astfel dă suma costurilor de substituție de-a lungul marginilor arborelui care se află sub vârful v, cu condiția ca vertexului v să i se atribuie Starea i. pentru rețelele filogenetice, pentru a ține cont de costurile de substituție de-a lungul marginilor care se află sub un vârf reticulat w doar o singură dată când vertexului v i se atribuie Starea i, lăsăm costurile de substituție de-a lungul tuturor marginilor care se află sub V. Pe de altă parte, dacă v nu este un părinte al lui w în arborele traversal, s(v, w)(i) denotă pur și simplu costul de substituție de la starea i la vârful v la o altă stare la w care este cel mai puțin costisitor.

definim apoi

unde suma se execută pentru toate nodurile copil(copii) w ale lui v. Așa cum am menționat anterior, în arborii filogenetici, S v (i) denotă suma minimă posibilă a costurilor de substituție de-a lungul tuturor marginilor de la vârful v la toate frunzele care sunt accesibile de la v, având în vedere că v este atribuit starea i și tuturor vârfurilor accesibile de la v li se atribuie fiecare o stare.

în rețelele filogenetice, în timp ce se calculează s(v, w)(i) unde w este un vârf reticulat astfel încât (v, w) nu este o margine în arborele traversal, nu există cunoștințe prealabile despre starea care va fi atribuită ulterior la vârful reticulat w. Astfel s(v, w) (i) poate fi doar o limită inferioară a marginilor rețelei care se află sub vârful v, dacă vertexului v i se atribuie starea i. raționamentul pentru aceasta este că s(v, w) (i) este costul de substituție de la starea i la vârful v la o altă stare la w care este cel mai puțin costisitor, în loc de costul de substituție de la starea i la v la starea la w care va fi atribuit ulterior. Deoarece definiția lui S v (i) depinde de definiția lui s(v, w) (i) și sunt definite recursiv, observăm următoarele: S v (i) este o limită inferioară a sumei costurilor de substituție de-a lungul marginilor rețelei care pot fi accesate de la vârful v, cu condiția ca v să i se atribuie starea i și tuturor vârfurilor arborelui descendent li se atribuie o stare unică, iar vârfurilor reticulate li se atribuie două stări care nu sunt neapărat aceleași. Stările atribuite ale vertexului reticulat contribuie la un conflict dacă stările nu sunt aceleași. Să presupunem că starea i este atribuită vertexului rădăcină r, iar tuturor vârfurilor arborelui li se atribuie o stare unică, în timp ce vârfurilor reticulate li se atribuie două stări. Apoi costul S r (i) denotă suma minimă posibilă a costurilor de substituție de-a lungul tuturor marginilor unui arbore transversal cu una dintre stările atribuite pentru vârfurile reticulate, plus suma costurilor de substituție de-a lungul marginilor reticulate rămase cu starea de atribuire alternativă la vârfurile reticulate. Deoarece căutăm o atribuire pe vârfurile rețelei fără conflicte în vârfurile reticulate, S r (i) este o limită inferioară a costului unei astfel de atribuiri în care vertexul rădăcină este atribuit i și toate vârfurile sunt atribuite cu o atribuire unică.

în această fază, stocăm și stările

pentru a putea urmări starea w care atinge cantitatea s(v, w)(i) în timpul fazei de precomandă. A Se Vedea Algoritmul 1.

precomandă faza de traversare: mai întâi alegem minimul

unde R este vârful rădăcină și atribuim starea care atinge minimul la vârful rădăcină, adică., fie hectolux ^ ( r ) = i r astfel încât S r (i r ) = S. pentru orice alt vârf w care nu este un vârf reticulat, al cărui părinte v este deja atribuit cu o stare i, atribuim starea t(v, w)(i). Pentru un nod reticulat w ale cărui noduri părinte sunt v și v’, să presupunem că v și v’ sunt atribuite stări I și i’ respectiv atunci când traversează prin precomandă. Stările posibile j = t(v, w)(i) și j’ = t(v’, w)(i’) din w care realizează s(v, w)(i) și s(v’, w)(i’) respectiv, nu trebuie să fie aceleași. Cu alte cuvinte, este posibil ca j j’. În acest caz, avem un conflict pe vertexul reticulat w. astfel, tehnica de programare dinamică nu reușește să dea o extensie pentru hectolix al cărui scor de parsimonie este S. În acest caz, alegem pur și simplu între j și j’ pentru XV(w) conform căruia dintre vârfurile dintre v și v’ este traversat mai întâi în Precomandă. Astfel, dacă vertexul w satisface condiția de traversare în raport cu v, avem un număr de x-x ^ ( w ) =j.

după finalizarea fazei de precomandă, putem obține scorul corespunzător extensiei x-x ^ setând mai întâi S ‘= S și actualizând S ‘ la fiecare vertex reticulat w după cum urmează: Scorul limitei superioare S’ este actualizat corespunzător atribuirii j la vertex w ca S’- c i’ j’ +c I ‘ j . A Se Vedea Algoritmul 2. Figura 2 prezintă un exemplu al modului în care algoritmul rulează într-o rețea. Din moment ce S r (i) este o limită inferioară pe atribuirea optimă unde vertexul rădăcină este atribuit i și toate vârfurile sunt atribuite cu o atribuire unică și din moment ce s = min I S r (i), concluzionăm că s este o limită inferioară a optimului pe care căutăm să-l găsim. A se vedea Lema 1 pentru o dovadă formală.

soluție de programare dinamică. Soluția de programare dinamică aplicată unei rețele filogenetice. Statele sunt 0, 1 și 2. Matricea de cost utilizată are toate 1s, cu excepția elementelor diagonale care sunt toate 0s. tabelele afișate pe fiecare vârf v sunt costurile, S v (i) (al doilea rând) al fiecărei stări, i (primul rând) care sunt calculate în timpul traversării post-comandă. De asemenea, afișate la vârfuri sunt stările copilului w, și anume t(v, w)(I) (al treilea rând) care corespund costurilor din al doilea rând; când există doi copii pentru un vârf, intrările din al treilea rând sunt reprezentate ca o pereche de stări ale copilului stâng și respectiv ale copilului drept. Fiecare margine(v, w) este etichetată cu s(v, w) (i) pentru fiecare stare i. în timpul traversării precomenzii, stările pentru fiecare vârf sunt selectate (afișate cu caractere aldine). Costul 2 evidențiat cu caractere aldine la vârful rădăcinii dă o limită inferioară, S. Starea atribuită la fiecare vârf este evidențiată cu caractere aldine. Algoritmul găsește un total de trei substituții (evidențiate prin margini îndrăznețe). Acest lucru se datorează faptului că stările atribuite la vârfurile părinte ale vârfului reticulat dau atribuiri conflictuale de 1 și respectiv 2, din care starea 1 este atribuită la vârful reticulat. Astfel, cu un cost suplimentar de 1, obținem scorul de 3 (o limită superioară a scorului optim) ca scor de parsimonie corespunzător atribuirii afișate. Rețineți că scorul optim de parsimonie în rețea este 2 (Egal cu limita inferioară), care poate fi găsit prin căutare exhaustivă și poate fi realizat prin schimbarea atribuirii de la 1 la 2 pentru părintele stâng al vârfului reticulat și de la 1 la 2 pentru vârful reticulat. Astfel, limita inferioară se potrivește cu scorul optim, deși atribuirea corespunzătoare limitei inferioare nu este lipsită de conflicte și nu este aceeași cu atribuirea corespunzătoare optimului.

Lema 1. Cantitatea S este o limită inferioară a scorului optim de parsimonie din rețeaua N.

dovada. De construcții de S, avem

în cazul în care cel de-al doilea sumand este pentru reticulate nod w cu părinții v și v’, v satisface traversare condiție w.r.t. w. Astfel, costul c λ ^ ( v ) , λ ^ ( w ) este substituirea costului de alocat de stat λ ^ ( v ), la v de stat λ ^ ( w ) la w. Pe de altă parte, costul c λ ^ ( v ‘) , t ( v ‘, w ) ( λ ^ ( v ‘) ) este substituirea costului de alocat de stat λ ^ ( v ), la v de stat t ( v ‘, w ) ( λ ^ ( v ‘ ) ) la w. Rețineți că starea t ( v ‘, w ) ( λ ^ ( v ‘ ) ) nu este neapărat aceeași ca statul λ ^ ( w ) , iar S este minim printre toate sarcinile care pot rezulta în conflicte la reticulate noduri.

Să presupunem că s ^ este scorul optim de parsimonie pe N cu funcția: v (n) {0, 1, …, / XV / – 1} ca extensie a lui XV avem

unde în al doilea summand W este un vârf reticulat cu părinții v și v’. Din moment ce XV este o sarcină fără conflicte care este conținută în setul tuturor sarcinilor dintre ale căror costuri S este minimul (comparați ecuația (3) și (4)) Avem s Inktoux s ^ . acum, pentru complexitatea algoritmului. Să presupunem că rețeaua N are n frunze și R vârfuri reticulate. Apoi numărul de vârfuri din N este 2 (n + r) -1. La fiecare vertex v și pentru fiecare stare i, cantitatea S poate fi calculată în O(k2) timp, unde k = |Hectol|. Pasul de traversare precomandă implică găsirea S în O (k) complexitate și atribuirea celor mai bune stări pentru fiecare nod. De asemenea, fixarea stărilor de noduri reticulate conflictuale necesită O(r) timp. Astfel, complexitatea algoritmului (prezentat aici)pentru a găsi o limită inferioară și superioară este o((n + r) k2). O limită superioară alternativă poate fi obținută în O(nk2) prin simpla atribuire în timpul fazei de traversare post-comandă, pentru fiecare vârf reticulat starea care apare de numărul maxim de ori la frunzele accesibile de la vârful reticulat respectiv; și procedând prin găsirea S v (i) pentru vârfurile rămase. Optimul exact poate fi obținut și prin restricționarea stărilor posibile la o singură stare pentru fiecare vârf reticulat, prin rularea algoritmului de programare dinamică pentru fiecare dintre combinațiile kr de stări pentru vârfurile reticulate și alegerea minimului dintre toate. Complexitatea în timp a acestui proces este O(nkr+2).

algoritm 1 faza de traversare Post-comandă: se calculează costul fiecărei stări la fiecare vârf

1. 1:

   intrare: rețea N și stările observate de la XV la frunzele lui N, adică, o funcție de atribuire a stării de la XV peste alfabetul de la N.

2. 2:

   pentru fiecare frunză de V, fie S v (i) = 0 dacă este cazul, dacă este cazul, în cazul lui.

3. 3:

   repetați în post-ordine pentru fiecare în vertex intern (rădăcină, nod arbore intern sau vertex reticulat) v în N: Pentru fiecare stare i, calculați S v (i) dat în(1) și t(v, w) (i) pentru fiecare copil w din v, dat în (2).

4. 4:

   ieșire: {(S v (i), ): v, v (n), v (n), i, v}.

minimizarea numărului de mutații pe o rețea filogenetică

algoritmul Fitch numără numărul de modificări într-un arbore filogenetic bifurcat pentru orice set de caractere, unde stările se pot schimba de la orice stare la orice altă stare. Astfel, matricea de cost este astfel încât elementele sale diagonale sunt toate zerouri, iar elementele off-diagonale sunt toate cele. În această secțiune, arătăm cum Algoritmul lui Fitch se extinde la găsirea limitelor superioare și inferioare pentru numărul de schimbări evolutive într-o rețea filogenetică dată. În primul rând, arătăm că algoritmul Fitch poate fi extins pentru a da o limită superioară pentru scorul optim de parsimonie. Ca și înainte, fazele de traversare post-comandă și precomandă sunt date în algoritmii 3 și 4 de mai jos. A se vedea Figura 3 pentru un exemplu de rulare a algoritmului.

soluție de tip Fitch. Soluția de tip Fitch aplicată aceleiași rețele filogenetice și datelor leaf din Figura 2. Fiecărui nod i se atribuie un set de toate stările posibile, împreună cu un scor atunci când nodurile de rețea sunt traversate în post-ordine. Scorul de la rădăcină oferă o limită superioară pentru scorul optim. Misiunile de stat sunt date în timpul fazei de traversare precomandă, iar numărul de substituții se potrivește cu scorul de la rădăcină.

algoritmul 2 faza de traversare precomandă: Se calculează limitele inferioare și superioare ale optimului și atribuirea corespunzătoare a limitei superioare

1. 1:

   intrare: {(S v (i), ): v inktv (n), i inktv}.

2. 2:

   fie S = min I S r ( i), unde r este vertexul rădăcinii și fie ^ (R ) =ARG min I S r (i ) .

3. 3:

   fie S’ = S

4. 4:

   pentru fiecare nod w în Precomandă al cărui nod părinte v precede imediat w în Precomandă, fie ca:

5. 5:

   vizitați fiecare vârf reticulat w cu părinții v și v’ astfel încât w să satisfacă condiția de traversare în raport cu v, cu i= hectolitri ^ ( v ) , i ‘= XIII ^ ( v ‘) , j ‘= t ( v ‘, w ) ( i ) și actualizați S’ după cum urmează:

   s ‘XIII S’ – C i ‘ j ‘+ c i ‘ J .
6. 6:

   ieșire: (limita inferioară, limita superioară) = (S, S’); extensie corespunzătoare scorului limitei superioare S ‘ : inqu ^ .

algoritmul 3 faza de traversare Post-comandă: calculați optimul

1. 1:

   intrare: Rețeaua filogenetică N și o funcție de atribuire a stării de pe alfabetul de pe alfabetul de pe N.

2. 2:

   pentru fiecare frunză v de N, ni se dă A(V) = {XV(v)}, un set singleton care conține starea observată la frunză.

3. 3:

   Set UB = 0.

4. 4:

   Recursa folosind post-comanda: pentru un vertex v de T cu copii w1 și w2, fie și dacă vertexul v are un singur copil w, atunci

și

5: ({a(v): v v (n)}, UB)

deoarece faza de traversare precomandă dă o atribuire fără conflicte pe vârfuri, UB este o limită superioară. Acesta este un caz special al algoritmului dinamic prezentat pentru matricea generală a costurilor. Să presupunem că restricționăm N pentru a fi o rețea filogenetică fără reticulări surori, atunci orice soluție Fitch pe orice arbore T în T (N ) formează o limită inferioară pentru scorul optim pe rețele; și adăugarea costului pe margini nu în T oferă o limită superioară pentru scorul optim. Astfel, este posibil să se calculeze limita noastră inferioară pentru numărarea numărului de modificări de caractere numai pentru rețelele filogenetice fără reticulări surori, unde este simplu să găsim un copac în T ( N ) .

algoritmul 4 faza de traversare precomandă: atribuirea stărilor

1. 1:

   intrare: arbore filogenetic N și ({a(v): v v (n)}, UB).

2. 2:

   pentru fiecare vârf v din arbore care nu este deja atribuit, algoritmul calculează ecuația ^ ( v ) după cum urmează: Pentru rădăcina R, (R) =(R), unde (R) este un element arbitrar al lui A (R). Atribuiți recursiv prin precomandă: pentru un vertex v al cărui părinte u este atribuit,

   XV ^ ( v ) = XV ^ ( u ) în cazul în care a ( V) A ( V ) ; A ( V ) în caz contrar .

3. 3:

   fixarea scorului: pentru fiecare vertex reticulat v, dacă u’ nu este părintele în precomandă și dacă u’) a ( V), dar u’) a ( V), apoi incrementați UB cu 1.

4. 4:

   ieșire: UB și funcția de extensie de la SEC.