V této části se budeme učit, jak vytvořit a použít jednoduchou lineární regresní model přeměnou prediktor x hodnoty. To může být první věc, kterou vyzkoušíte, pokud ve svých datech najdete nelineární trend. To znamená, že transformace hodnot x je vhodná, pokud je jediným problémem nelinearita (tj. jsou splněny podmínky nezávislosti, normality a rovného rozptylu). Všimněte si však, že může být nutné opravit nelinearitu, než budete moci posoudit předpoklady normality a stejné rozptylu. Taky, zatímco některé předpoklady se mohou zdát, že drží před aplikací transformace, po uplatnění transformace již nemusí držet. Jinými slovy, použití transformací je součástí iterativního procesu, kde jsou všechny předpoklady lineární regrese po každé iteraci znovu zkontrolovány.
Mějte na paměti, že i když jsme se zaměřením na jednoduchý lineární regresní model, základní myšlenky platí obecněji pro vícenásobné lineární regresní modely. Můžeme uvažovat o transformaci některého z prediktorů zkoumáním scatterplotů zbytků oproti každému prediktoru.
vytvoření modelu
příklad. Nejjednodušší způsob, jak se dozvědět o transformacích dat, je příklad. Uvažujme o datech z experimentu s uchováním paměti, ve kterém bylo 13 subjektů požádáno o zapamatování seznamu odpojených položek. Subjekty byly poté požádány, aby si položky stáhly v různých časech až o týden později. Podíl položek (y = prop) správně připomenout v různých časech (x = Čas, v minutách), protože seznam byl uložen do paměti byly zaznamenány (wordrecall.txt) a vyneseno. Uznávajíce, že neexistuje žádný dobrý důvod, že chyba hlediska by nemělo být nezávislé, pojďme zhodnotit zbývající tři podmínky — linearita, normality a rovností rozptylů — modelu.
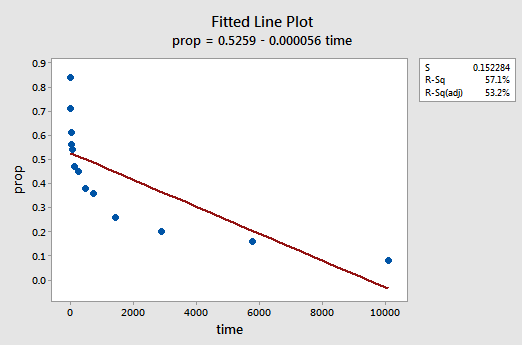
výsledná fitted line plot naznačuje, že podíl připomíná položky (y) je přímo úměrná času (x):
graf rezidua vs. zapadá děj také naznačuje, že vztah není lineární:
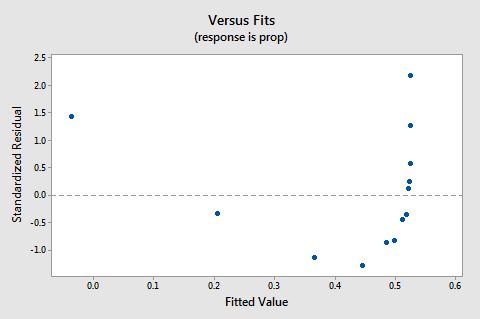
Protože nedostatek linearity dominuje děj, nemůžeme použít spiknutí s cílem vyhodnotit, zda je nebo není chyba rozptyly jsou stejné. Musíme vyřešit problém nelinearity, než budeme moci posoudit předpoklad stejných odchylek.
a co normální pravděpodobnostní graf zbytků? Co to naznačuje o chybových termínech? Můžeme dojít k závěru, že jsou normálně distribuovány?
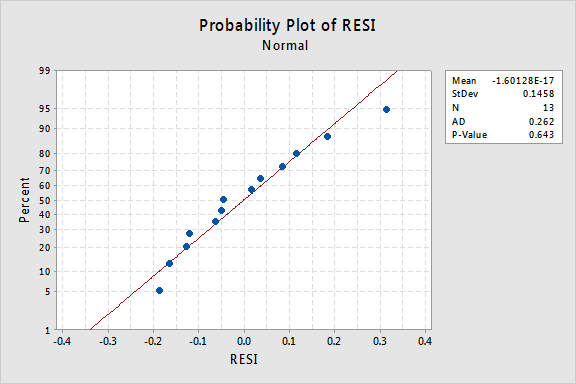
Anderson-Darling P-hodnota pro tento příklad je 0.643, což naznačuje, že nejsme schopni zamítnout nulovou hypotézu o normálním chybové podmínky. Neexistuje dostatek důkazů k závěru, že podmínky chyby nejsou normální.
V souhrnu máme datovou sadu, ve které je nelinearita jediným závažným problémem. Tato situace křičí na transformaci pouze hodnot prediktoru. Než tak učiníme, pojďme stranou a diskutovat o „logaritmické transformaci“, protože se jedná o nejběžnější a nejužitečnější dostupnou transformaci dat.
logaritmická transformace. Výchozí logaritmická transformace zahrnuje pouze převzetí přirozeného logaritmu-označeného ln nebo loge nebo jednoduše log-každé datové hodnoty. Dalo by se uvažovat o jiném druhu logaritmu, jako je log base 10 nebo log base 2. Přirozený logaritmus-který lze považovat za logovou základnu e, kde e je konstanta 2.718282… – je nejběžnější logaritmická stupnice používaná ve vědecké práci.
obecné charakteristiky přirozené logaritmické funkce jsou:
- přirozený logaritmus x, je energie e = 2.718282… že budete muset vzít s cílem získat x. To může být uvedeno notationally jako ln(ex) = x. Například, přirozený logaritmus 5 je moc, na které budete muset zvýšit e = 2.718282… za účelem získání 5. Protože 2.7182821.60944 je přibližně 5, říkáme, že přirozený logaritmus 5 je 1.60944. Notářsky říkáme ln (5) = 1.60944.
- přirozený logaritmus e se rovná jednomu, tj. ln (e) = 1.
- přirozený logaritmus jedničky se rovná nule, tedy ln (1) = 0.
graf přirozeného logaritmu funkce:
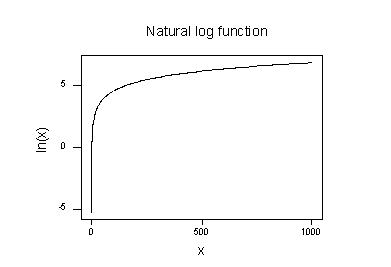
naznačují, že účinky užívání přírodních logaritmické transformace jsou:
- Malé hodnoty, které jsou blízko u sebe se šíří dál.
- velké hodnoty, které jsou rozloženy, jsou sblíženy.
zpět na příklad. Použijme přirozený logaritmus k transformaci hodnot x v datech experimentu uchovávání paměti. Protože X = time je prediktor, vše, co musíme udělat, je vzít přirozený logaritmus každé časové hodnoty, která se objeví v datové sadě. Přitom jsme se vytvořit nově transformované prediktor nazývá lntime:
| čas | prop | lntime |
| 1 | 0.84 | 0.00000 |
| 5 | 0.71 | 1.60944 |
| 15 | 0.61 | 2.70805 |
| 30 | 0.56 | 3.40120 |
| 60 | 0.54 | 4.09434 |
| 120 | 0.47 | 4.78749 |
| 240 | 0.45 | 5.48064 |
| 480 | 0.38 | 6.17379 |
| 720 | 0.36 | 6.57925 |
| 1440 | 0.26 | 7.27240 |
| 2880 | 0.20 | 7.96555 |
| 5760 | 0.16 | 8.65869 |
| 10080 | 0.08 | 9.21831 |
We take the natural logarithm for each value of time and place the results in their own column. To znamená, že „transformujeme“ každou časovou hodnotu prediktoru na hodnotu ln (čas). Například ln (1) = 0, ln(5) = 1.60944 a ln (15) = 2.70805 atd.
Nyní, když jsme transformovali hodnoty prediktoru, uvidíme, jestli to pomohlo opravit nelineární trend v datech. Model jsme znovu přizpůsobili y = prop jako odpověď a x = lntime jako prediktor.
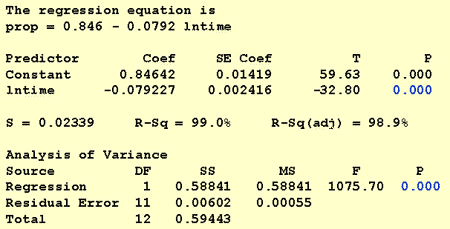
výsledný graf osazené čáry naznačuje, že je užitečné vzít přirozený logaritmus hodnot prediktoru.
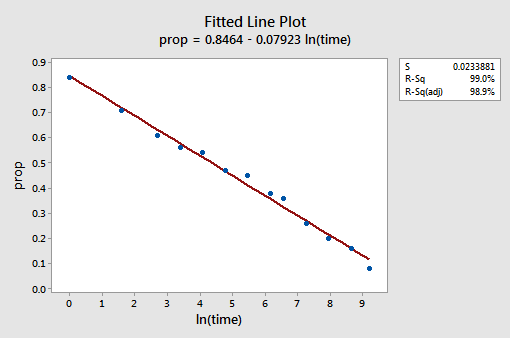
Opravdu, R2 hodnota se zvýšila z 57.1% 99.0%. Říká nám, že 99% variací v podílu vzpomínaných slov (prop) je sníženo zohledněním přirozeného protokolu času (lntime)!
nový graf residual vs. fits ukazuje významné zlepšení oproti grafu založenému na netransformovaných datech.
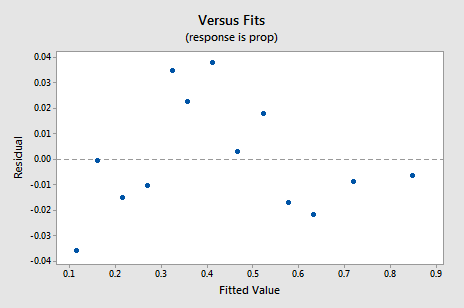
Ty by se mohly stát obavy o nějaký druh nahoru-dolů cyklický trend v grafu. Znovu vás varuji, abyste tyto grafy příliš neinterpretovali, zvláště když je datová sada takto malá. Opravdu byste neměli očekávat dokonalost, když se uchýlíte k provádění datových transformací. Někdy se musíte spokojit s významnými vylepšeními. Mimochodem, spiknutí také naznačuje, že je v pořádku předpokládat, že odchylky chyb jsou stejné.
normální pravděpodobnostní graf zbytků ukazuje, že transformace hodnot x neměla žádný vliv na normálnost chybových výrazů:
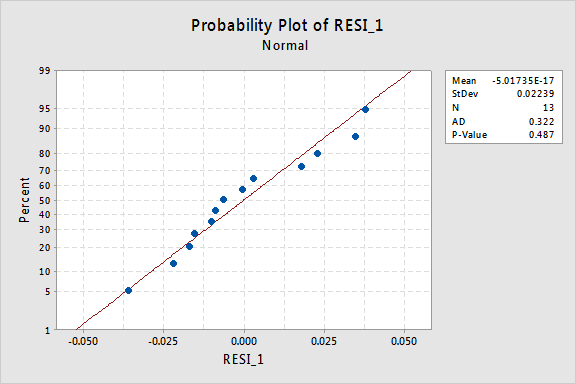
Opět Anderson-Darling P-hodnota je velký, takže se nám nepodaří nulovou hypotézu zamítnout normální chybové podmínky. Neexistuje dostatek důkazů k závěru, že podmínky chyby nejsou normální.
Co kdybychom místo toho transformovali hodnoty y? Dříve jsem řekl, že zatímco některé předpoklady se mohou zdát, že drží před aplikací transformace, po uplatnění transformace již nemusí držet. Pokud jsou například chybové výrazy dobře vychované, transformace hodnot y by je mohla změnit na špatně chované chybové výrazy. Chybové výrazy pro data Uchování paměti před transformací hodnot x se zdají být dobře vychované (v tom smyslu, že se zdají být přibližně normální). Proto bychom mohli očekávat, že transformace hodnot y namísto hodnot x by mohla způsobit špatné chování chybových výrazů. Podívejme se rychle na data uchovávání paměti, abychom viděli příklad toho, co se může stát, když transformujeme hodnoty y, když je jediným problémem nelinearita.
pokusem a omylem zjistíme, že mocninová transformace y, která dělá nejlepší práci při korekci nelinearity, je y-1,25. Vybavená line plot ukazuje, že transformace skutečně narovnat vztah — i když sice ne tak dobře jako log transformace hodnoty x.
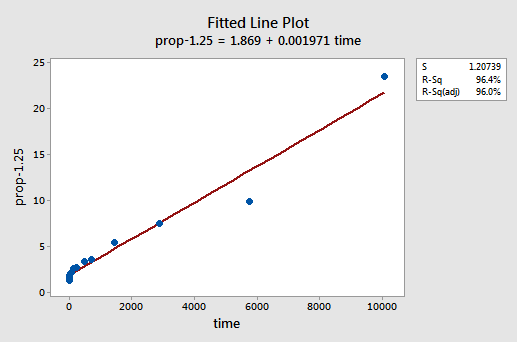
Všimněte si, že R2 hodnota se zvýšila z 57.1% 96.4%.
zbytky vykazují zlepšení s ohledem na nelinearitu, i když zlepšení není velké…
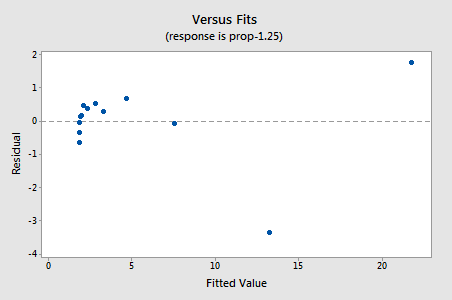
…ale teď máme neobvyklé chybové termíny! Andersonova-Darlingova p-hodnota je menší než 0,005, takže odmítáme nulovou hypotézu normálních chybových výrazů. Existuje dostatek důkazů k závěru, že chyba podmínky nejsou normální:
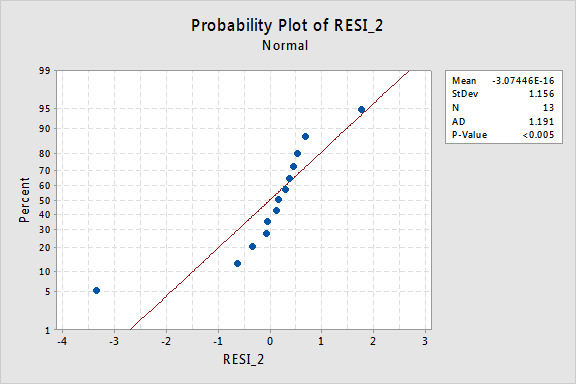
Opět platí, že pokud chyba termíny jsou dobře-choval před transformace, transformace y hodnoty se mohou měnit je do špatně vychovaný chybové podmínky.
pomocí modelu
jakmile najdeme nejlepší model pro naše regresní data, můžeme tento model použít k zodpovězení našich výzkumných otázek. Pokud náš model zahrnuje transformované hodnoty prediktoru (x), můžeme nebo nemusíme provádět drobné úpravy standardních postupů, které jsme se již naučili.
použijme náš lineární regresní model pro data uchovávání paměti-s y = prop jako odpovědí a x = lntime jako prediktorem-k zodpovězení čtyř různých výzkumných otázek.
Výzkumná otázka #1: Jaká je povaha vztahu mezi časem od zapamatování a účinností odvolání?
odpovědět Na tuto výzkumnou otázku jsme se jen popsat povahu tohoto vztahu. To znamená, že podíl správně připomněl slova je negativně úměrná přirozenému logaritmu času od slova nazpaměť. Není divu, že s rostoucím přirozeným záznamem času klesá podíl vzpomínaných slov.
Výzkumná otázka #2: Existuje souvislost mezi časem od zapamatování a účinností odvolání?
při zodpovězení této výzkumné otázky není nutná žádná úprava standardního postupu. My jen test nulové hypotézy H0: β1 = 0 buď pomocí F-testu nebo ekvivalent t-test:
Jako softwarový výstup ukazuje, P-hodnota je < 0.001. Existují významné důkazy na 0.05 úrovni k závěru, že existuje lineární vztah mezi podílem připomněl slova a přirozený logaritmus času, od paměti.
Výzkumná otázka #3: jaký podíl slov můžeme očekávat, že si náhodně vybraná osoba vzpomene po 1000 minutách?
stačí vypočítat interval predikce – s jednou malou modifikací-abychom odpověděli na tuto výzkumnou otázku. Naše prediktorová proměnná je přirozený logaritmus času. Proto, když budeme používat statistický software pro výpočet predikce intervalu, musíme se ujistit, že máme určit hodnotu prediktor hodnot v transformovaných jednotek, není původní jednotky. Přirozený protokol 1000 minut je 6,91 log-minut. Pomocí software vypočítat 95% predikční interval, kdy lntime = 6.91, dostaneme:
výstup nám říká, že můžeme být na 95% jisti, že po 1000 minut, náhodně vybraný člověk bude připomeňme mezi 24.5% a 35.3% slov.
Výzkumná otázka č. 4: Kolik se očekávané stažení změní, pokud se čas zvýší desetkrát?
pokud o tom přemýšlíte, odpověď na tuto výzkumnou otázku zahrnuje pouze odhad a interpretaci parametru svahu β1. No, ne tak docela—dochází k mírnému přizpůsobení. Obecně platí, že k-násobné zvýšení v prediktor x je spojena s:
β1 × ln(k)
změna v průměrné odezvy y.
Toto odvození vyplývá, že by ti mohlo pomoci pochopit a proto nezapomeňte tento vzorec.
To je ten-násobné zvýšení v x souvisí s β1 × ln(10) změna v y. A, dva-násobný nárůst x souvisí s β1 × ln(2) změna v y.
obecně platí, že byste měli používat pouze násobky k, které mají smysl pro rozsah modelu. Pokud se například hodnoty x ve vaší datové sadě pohybují od 2 do 8, má smysl uvažovat pouze o násobcích k, které jsou 4 nebo menší. Pokud by hodnota x byla 2, desetinásobné zvýšení (tj. k = 10) by vás vedlo od 2 do 2 × 10 = 20, což je hodnota mimo rozsah modelu. V datové sadě pro uchování paměti se hodnoty prediktoru pohybují od 1 do 10080, takže není problém uvažovat o desetinásobném zvýšení.
Když jsme se zajímají pouze o získání bodový odhad, můžeme pouze vzít odhad svahu parametr (b1 = -0.079227) ze softwaru výstup:

a vynásobím to tím, že ln(10):
b1 × ln(10) = -0.079227 × ln(10) = -0.182
očekáváme, že procento připomenout slova k poklesu (od znamení je negativní) 18.2% za každé desetinásobné zvýšení času od doby, kdy došlo k zapamatování.
Tento bodový odhad má samozřejmě omezenou užitečnost. Jak si můžeme být jisti, že odhad se blíží skutečné neznámé hodnotě? Samozřejmě bychom měli vypočítat 95% sebevědomý interval. Za tímto účelem vypočítáme 95% interval spolehlivosti pro β1, jak vždy máme: