i dette afsnit lærer vi, hvordan man bygger og bruger en simpel lineær regressionsmodel ved at transformere predictor-værdierne. Dette kan være den første ting, du prøver, hvis du finder en ikke-lineær tendens i dine data. Det vil sige, at transformation af værdierne er passende, når ikke-linearitet er det eneste problem (dvs.betingelserne for uafhængighed, normalitet og lige varians er opfyldt). Bemærk dog, at det kan være nødvendigt at rette op på ikke-lineariteten, før du kan vurdere normaliteten og antagelserne om lige varians. Selvom nogle antagelser kan synes at holde, før de anvender en transformation, kan de muligvis ikke længere holde, når en transformation er anvendt. Med andre ord er brug af transformationer en del af en iterativ proces, hvor alle de lineære regressionsforudsætninger kontrolleres igen efter hver iteration.
Husk, at selvom vi fokuserer på en simpel lineær regressionsmodel her, gælder de væsentlige ideer mere generelt også for flere lineære regressionsmodeller. Vi kan overveje at omdanne nogen af forudsigerne ved at undersøge scatterplots af resterne versus hver forudsigelse igen.
opbygning af modellen
et eksempel. Den nemmeste måde at lære om datatransformationer er ved eksempel. Lad os overveje dataene fra et hukommelsesopbevaringseksperiment, hvor 13 emner blev bedt om at huske en liste over frakoblede emner. Emnerne blev derefter bedt om at huske emnerne på forskellige tidspunkter op til en uge senere. Andelen af elementer (y = prop) korrekt tilbagekaldt på forskellige tidspunkter (tid, i minutter) siden listen blev gemt blev registreret (ordindkaldelse.tekst) og plottet. At erkende, at der ikke er nogen god grund til, at fejlbetingelserne ikke ville være uafhængige, lad os evaluere de resterende tre betingelser — linearitet, normalitet og lige afvigelser — af modellen.
det resulterende monterede linjeplot antyder, at andelen af tilbagekaldte genstande (y) ikke er lineært relateret til tiden:
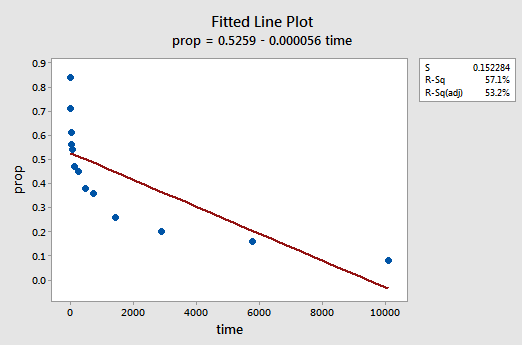
residualerne vs. passer plot foreslår også, at forholdet ikke er lineært:
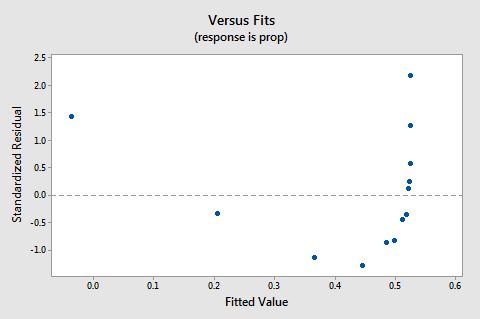
fordi manglen på linearitet dominerer plottet, kan vi ikke bruge plottet til at evaluere, om fejlafvigelserne er ens. Vi er nødt til at løse problemet med ikke-linearitet, før vi kan vurdere antagelsen om lige afvigelser.
hvad med den normale Sandsynlighed plot af resterne? Hvad antyder det om fejlbetingelserne? Kan vi konkludere, at de normalt distribueres?
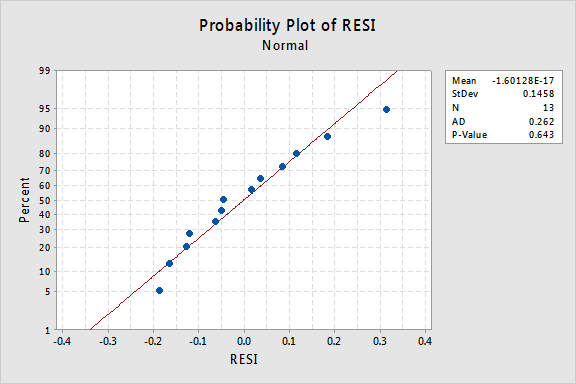
Anderson-Darling P-værdien for dette eksempel er 0,643, hvilket antyder, at vi ikke afviser nulhypotesen om normale fejlbetingelser. Der er ikke nok beviser til at konkludere, at fejlbetingelserne ikke er normale.
sammenfattende har vi et datasæt, hvor ikke-linearitet er det eneste store problem. Denne situation skriger ud for kun at transformere forudsigerens værdier. Før vi gør det, lad os tage en side og diskutere den “logaritmiske transformation”, da det er den mest almindelige og mest nyttige datatransformation, der er tilgængelig.
den logaritmiske transformation. Standardlogaritmisk transformation involverer blot at tage den naturlige logaritme-betegnet ln eller loge eller blot log — af hver dataværdi. Man kunne overveje at tage en anden slags logaritme, såsom log base 10 eller log base 2. Imidlertid er den naturlige logaritme-som kan betragtes som logbase e, hvor e er konstanten 2.718282… – er den mest almindelige logaritmiske skala, der anvendes i videnskabeligt arbejde.
de generelle egenskaber ved den naturlige logaritmiske funktion er:
- den naturlige logaritme er kraften i e = 2.718282… for eksempel er den naturlige logaritme på 5 den magt, som du skal hæve e = 2.718282… for at få 5. Da 2.7182821.60944 er cirka 5, siger vi, at den naturlige logaritme på 5 er 1.60944. Notationelt siger vi ln (5) = 1.60944.
- den naturlige logaritme af e er lig med en, det vil sige ln(e) = 1.
- den naturlige logaritme af en er lig med nul, det vil sige ln(1) = 0.
plottet for den naturlige logaritmefunktion:
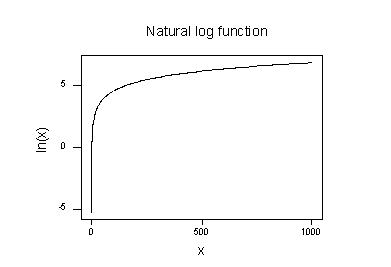
antyder, at virkningerne af at tage den naturlige logaritmiske transformation er:
- små værdier, der er tæt sammen, spredes længere ud.
- store værdier, der er spredt, bringes tættere sammen.
Tilbage til eksemplet. Lad os bruge den naturlige logaritme til at omdanne værdierne i hukommelsesopbevaringseksperimentdataene. Da tid er forudsigeren, er alt, hvad vi skal gøre, at tage den naturlige logaritme for hver tidsværdi, der vises i datasættet. Dermed opretter vi en nyligt transformeret forudsigelse kaldet lntime:
| time | prop | lntime |
| 1 | 0.84 | 0.00000 |
| 5 | 0.71 | 1.60944 |
| 15 | 0.61 | 2.70805 |
| 30 | 0.56 | 3.40120 |
| 60 | 0.54 | 4.09434 |
| 120 | 0.47 | 4.78749 |
| 240 | 0.45 | 5.48064 |
| 480 | 0.38 | 6.17379 |
| 720 | 0.36 | 6.57925 |
| 1440 | 0.26 | 7.27240 |
| 2880 | 0.20 | 7.96555 |
| 5760 | 0.16 | 8.65869 |
| 10080 | 0.08 | 9.21831 |
We take the natural logarithm for each value of time and place the results in their own column. Det vil sige, vi “transformerer” hver forudsigelsestidsværdi til en Ln(tid) værdi. For eksempel ln(1) = 0, ln(5) = 1.60944 og ln(15) = 2.70805 osv.
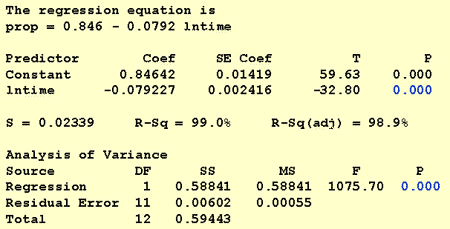
nu hvor vi har transformeret forudsigelsesværdierne, lad os se, om det hjalp med at korrigere den ikke-lineære tendens i dataene. Vi re-fit modellen med y = prop som svar og H = lntime som prædiktor.
det resulterende monterede linjeplot antyder, at det er nyttigt at tage den naturlige logaritme af forudsigelsesværdierne.
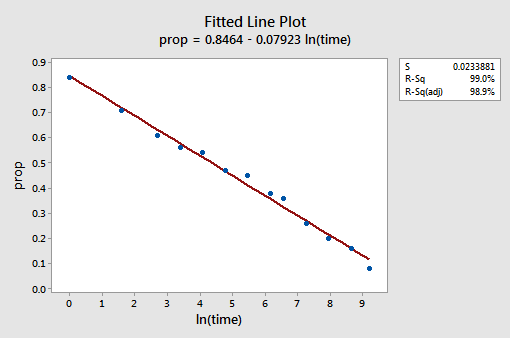
faktisk er R2-værdien steget fra 57,1% til 99,0%. Det fortæller os, at 99% af variationen i andelen af tilbagekaldte ord (prop) reduceres ved at tage hensyn til den naturlige log af tid (lntime)!
det nye resterende vs. fits-plot viser en signifikant forbedring i forhold til den, der er baseret på de ikke-transformerede data.
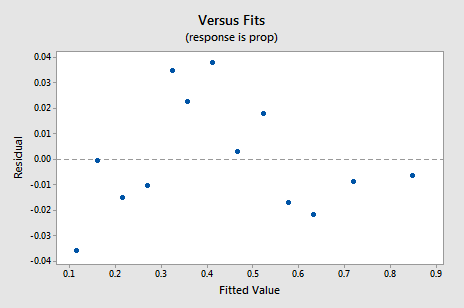
Du kan blive bekymret for en slags op-ned cyklisk tendens i plottet. Jeg advarer dig igen om ikke at overfortolke disse plot, især når datasættet er lille som dette. Du bør virkelig ikke forvente perfektion, når du ty til at tage datatransformationer. Nogle gange skal du bare være tilfreds med betydelige forbedringer. Forresten antyder plottet også, at det er okay at antage, at fejlafvigelserne er ens.
residualernes normale sandsynlighedsplot viser, at transformering af H-værdierne ikke havde nogen indflydelse på normaliteten af fejlbetingelserne:
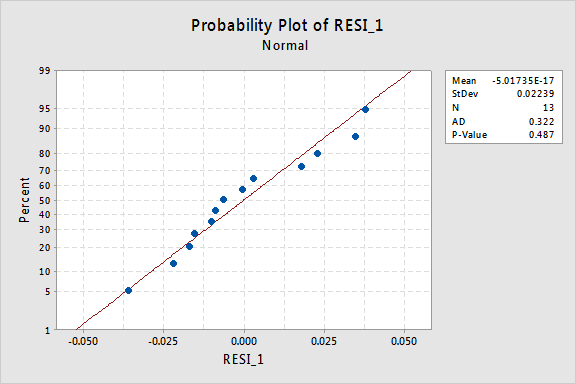
igen er Anderson-Darling P-værdien stor, så vi undlader at afvise nulhypotesen om normale fejlbetingelser. Der er ikke nok beviser til at konkludere, at fejlbetingelserne ikke er normale.
Hvad hvis vi havde transformeret y-værdierne i stedet? Tidligere sagde jeg, at mens nogle antagelser kan synes at holde før anvendelse af en transformation, kan de ikke længere holde, når en transformation er anvendt. For eksempel, hvis fejlbetingelserne er velopdragen, kan omdannelse af y-værdierne ændre dem til dårligt opførte fejlbetingelser. Fejlbetingelserne for hukommelsesopbevaringsdataene før omdannelse af værdierne ser ud til at være velopdragen (i den forstand, at de forekommer omtrent normale). Derfor kan vi forvente, at omdannelse af Y-værdierne i stedet for H-værdierne kan medføre, at fejlbetingelserne bliver dårligt opførte. Lad os se hurtigt på hukommelsesopbevaringsdataene for at se et eksempel på, hvad der kan ske, når vi transformerer y-værdierne, når ikke-linearitet er det eneste problem.
ved forsøg og fejl opdager vi, at krafttransformationen af y, der gør det bedste job til at korrigere ikke-lineariteten, er y-1.25. Det monterede linjeplot illustrerer, at transformationen faktisk retter forholdet ud — selvom det ganske vist ikke er så godt som logtransformationen af H-værdierne.
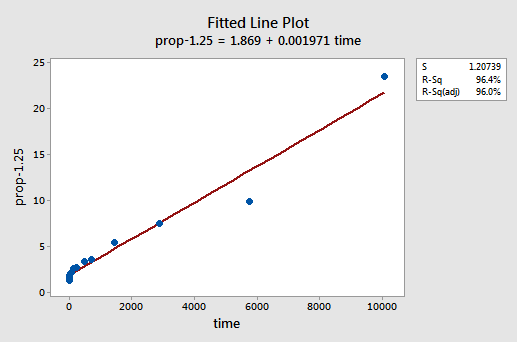
Bemærk, at R2-værdien er steget fra 57.1% til 96.4%.
restprodukterne viser en forbedring med hensyn til ikke-linearitet, selvom forbedringen ikke er stor…
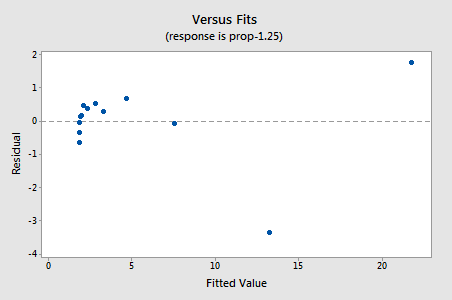
…men nu har vi ikke-normale fejlbetingelser! Anderson-Darling P-værdien er mindre end 0,005, så vi afviser nulhypotesen om normale fejlbetingelser. Der er tilstrækkelig dokumentation til at konkludere, at fejlbetingelserne ikke er normale:
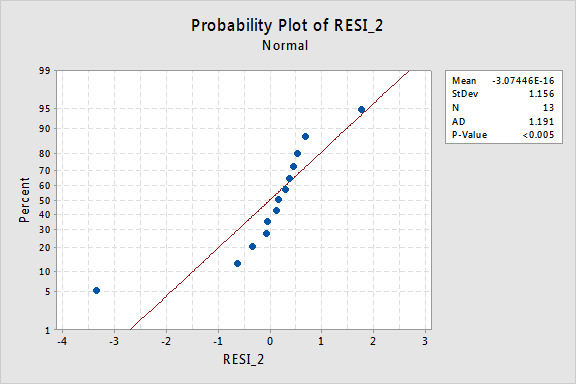
igen, hvis fejlbetingelserne er velopdragen før transformation, kan omdannelse af y-værdierne ændre dem til dårligt opførte fejlbetingelser.
brug af modellen
Når vi har fundet den bedste model til vores regressionsdata, kan vi derefter bruge modellen til at besvare vores forskningsspørgsmål af interesse. Hvis vores model involverer transformerede forudsigelsesværdier, er vi muligvis ikke nødt til at foretage små ændringer af de standardprocedurer, vi allerede har lært.
lad os bruge vores lineære regressionsmodel til hukommelsesretentionsdata—med y = prop som svar og H = lntime som forudsigelse—til at besvare fire forskellige forskningsspørgsmål.
forskningsspørgsmål #1: Hvad er karakteren af sammenhængen mellem tid siden husket og effektiviteten af tilbagekaldelse?
for at besvare dette forskningsspørgsmål beskriver vi bare forholdet. Det vil sige, at andelen af korrekt tilbagekaldte ord er negativt lineært relateret til den naturlige log af tiden, siden ordene blev husket. Ikke overraskende, da den naturlige log af tid stiger, falder andelen af tilbagekaldte ord.
forskningsspørgsmål #2: er der en sammenhæng mellem tiden siden husket og effektiviteten af tilbagekaldelse?
ved besvarelse af dette forskningsspørgsmål er ingen ændring af standardproceduren nødvendig. Vi tester blot nulhypotesen H0: prist1 = 0 ved hjælp af enten F-testen eller den tilsvarende t-test:
som programudgangen illustrerer, er P-værdien < 0.001. Der er betydelige beviser på 0.05 niveau for at konkludere, at der er en lineær sammenhæng mellem andelen af tilbagekaldte ord og den naturlige log af tiden siden gemt.3: Hvilken andel af ord kan vi forvente, at en tilfældigt udvalgt person husker efter 1000 minutter?
vi skal bare beregne et forudsigelsesinterval — med en lille ændring-for at besvare dette forskningsspørgsmål. Vores forudsigelsesvariabel er den naturlige log over tid. Derfor, når vi bruger statistiske programmer til at beregne forudsigelsesintervallet, skal vi sørge for, at vi angiver værdien af forudsigelsesværdierne i de transformerede enheder, ikke de oprindelige enheder. Den naturlige log på 1000 minutter er 6,91 log-minutter. Når lntime = 6.91, opnår vi:
outputtet fortæller os, at vi kan være 95% sikre på, at vi, efter at have modtaget en 1000 minutter vil en tilfældigt udvalgt person huske mellem 24,5% og 35.3% af ordene.4: Hvor meget ændres den forventede tilbagekaldelse, hvis tiden stiger ti gange?
Hvis du tænker over det, involverer besvarelse af dette forskningsspørgsmål kun estimering og fortolkning af hældningsparameteren karr1. Nå, ikke helt-der er en lille justering. Generelt er en k-fold stigning i prædiktoren forbundet med en:
LR1 Ln(k)
ændring i middelværdien af svaret y.
denne afledning, der følger, kan hjælpe dig med at forstå og derfor huske denne formel.
det vil sige, at en ti gange stigning i H er forbundet med en ændring i RR1 Ln(10) i middelværdien af y. og en to gange stigning i H er forbundet med en ændring i RR1 ln(2) i middelværdien af y.
generelt bør du kun bruge multipler af k, der giver mening for modelens omfang. Hvis f.eks. værdierne i dit datasæt varierer fra 2 til 8, giver det kun mening at overveje k-multipler, der er 4 eller mindre. Hvis værdien af H var 2, ville en ti gange stigning (dvs.k = 10) tage dig fra 2 op til 2 list 10 = 20, en værdi uden for modelens anvendelsesområde. I hukommelsesretentionsdatasættet varierer forudsigelsesværdierne fra 1 til 10080, så der er ikke noget problem med at overveje en ti gange stigning.
hvis vi kun er interesserede i at opnå et punktestimat, tager vi kun estimatet af hældningsparameteren (b1 = -0.079227) fra programudgangen:

og multiplicerer det med ln(10):
B1 Ln(10) = -0.079227 Ln(10) = -0.182
Vi forventer, at procentdelen af tilbagekaldte ord falder (da tegnet er negativt) 18.2% for hver ti gange stigning i tiden siden memorisering fandt sted.
selvfølgelig er dette punktestimat af begrænset anvendelighed. Hvor sikre kan vi være på, at estimatet er tæt på den sande ukendte værdi? Naturligvis skal vi beregne et 95% selvsikker interval. For at gøre det beregner vi bare et 95% konfidensinterval for kr1, som vi altid har: