In diesem Abschnitt erfahren Sie, wie Sie ein einfaches lineares Regressionsmodell erstellen und verwenden, indem Sie die x-Werte des Prädiktors transformieren. Dies ist möglicherweise das erste, was Sie versuchen, wenn Sie einen nichtlinearen Trend in Ihren Daten finden. Das heißt, die Transformation der x-Werte ist angemessen, wenn die Nichtlinearität das einzige Problem ist (dh die Bedingungen für Unabhängigkeit, Normalität und gleiche Varianz erfüllt sind). Beachten Sie jedoch, dass es möglicherweise erforderlich ist, die Nichtlinearität zu korrigieren, bevor Sie die Annahmen zur Normalität und zur gleichen Varianz bewerten können. Während einige Annahmen vor dem Anwenden einer Transformation zu gelten scheinen, gelten sie möglicherweise nicht mehr, sobald eine Transformation angewendet wird. Mit anderen Worten, die Verwendung von Transformationen ist Teil eines iterativen Prozesses, bei dem alle linearen Regressionsannahmen nach jeder Iteration erneut überprüft werden.
Denken Sie daran, dass, obwohl wir uns hier auf ein einfaches lineares Regressionsmodell konzentrieren, die wesentlichen Ideen allgemeiner auch für multiple lineare Regressionsmodelle gelten. Wir können erwägen, einen der Prädiktoren zu transformieren, indem wir Streudiagramme der Residuen gegenüber jedem Prädiktor der Reihe nach untersuchen.
Erstellen des Modells
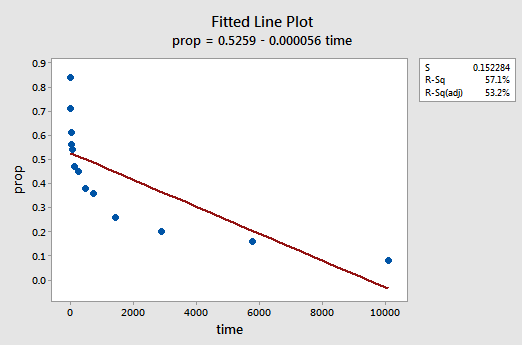
Ein Beispiel. Der einfachste Weg, etwas über Datentransformationen zu lernen, ist das Beispiel. Betrachten wir die Daten aus einem Experiment zur Gedächtniserhaltung, bei dem 13 Probanden gebeten wurden, sich eine Liste nicht verbundener Elemente zu merken. Die Probanden wurden dann gebeten, sich bis zu einer Woche später zu verschiedenen Zeiten an die Gegenstände zu erinnern. Der Anteil der Elemente (y = prop) korrekt zu verschiedenen Zeiten abgerufen (x = Zeit, in Minuten), da die Liste gespeichert wurden aufgezeichnet (wordrecall.txt) und geplottet. Wenn wir erkennen, dass es keinen guten Grund dafür gibt, dass die Fehlerterme nicht unabhängig wären, bewerten wir die verbleibenden drei Bedingungen — Linearität, Normalität und gleiche Varianzen — des Modells.
Das resultierende angepasste Liniendiagramm legt nahe, dass der Anteil der zurückgerufenen Artikel (y) nicht linear mit der Zeit (x) zusammenhängt:
Das Residuen-vs. Fits-Diagramm legt auch nahe, dass die Beziehung nicht linear ist:
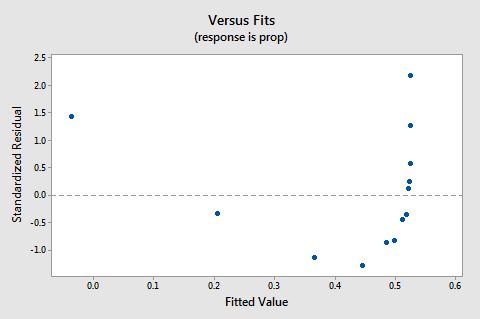
Da die fehlende Linearität das Diagramm dominiert, können wir das Diagramm nicht verwenden, um zu bewerten, ob die Fehlervarianzen gleich sind oder nicht. Wir müssen das Nichtlinearitätsproblem beheben, bevor wir die Annahme gleicher Varianzen beurteilen können.
Was ist mit dem Normalwahrscheinlichkeitsdiagramm der Residuen? Was sagt es über die Fehlerbedingungen aus? Können wir daraus schließen, dass sie normalverteilt sind?
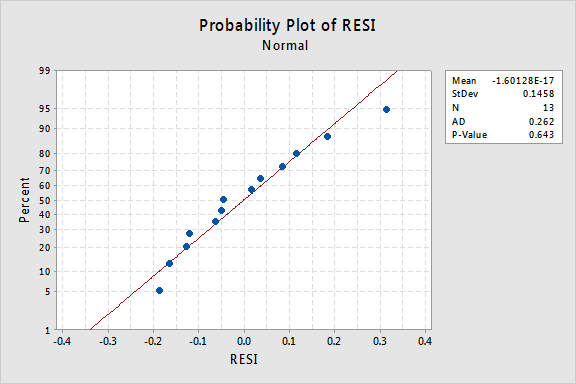
Der Anderson-Darling-P-Wert für dieses Beispiel ist 0,643, was darauf hindeutet, dass wir die Nullhypothese normaler Fehlerterme nicht ablehnen können. Es gibt nicht genügend Beweise, um zu dem Schluss zu kommen, dass die Fehlerbedingungen nicht normal sind.
Zusammenfassend haben wir einen Datensatz, in dem Nichtlinearität das einzige große Problem ist. Diese Situation schreit danach, nur die Werte des Prädiktors zu transformieren. Bevor wir dies tun, lassen Sie uns beiseite nehmen und die „logarithmische Transformation“ diskutieren, da es die häufigste und nützlichste verfügbare Datentransformation ist.
Die logarithmische Transformation. Bei der standardmäßigen logarithmischen Transformation wird lediglich der natürliche Logarithmus — bezeichnet als ln oder loge oder einfach log — jedes Datenwerts verwendet. Man könnte in Betracht ziehen, eine andere Art von Logarithmus zu verwenden, z. B. log base 10 oder log base 2. Der natürliche Logarithmus — der als Log-Basis e betrachtet werden kann, wobei e die Konstante 2,718282 ist… – ist die häufigste logarithmische Skala, die in wissenschaftlichen Arbeiten verwendet wird.
Die allgemeinen Eigenschaften der natürlichen logarithmischen Funktion sind:
- Der natürliche Logarithmus von x ist die Potenz von e = 2,718282… dies kann notationell als ln (ex) = x angegeben werden. Zum Beispiel ist der natürliche Logarithmus von 5 die Potenz, auf die Sie e = 2,718282 erhöhen müssen… um 5 zu bekommen. Da 2.7182821.60944 ungefähr 5 ist, sagen wir, dass der natürliche Logarithmus von 5 1.60944 ist. Notationell sagen wir ln (5) = 1,60944.
- Der natürliche Logarithmus von e ist gleich eins, dh ln(e) = 1.
- Der natürliche Logarithmus von eins ist gleich Null, dh ln(1) = 0.
Die Darstellung der natürlichen Logarithmusfunktion:
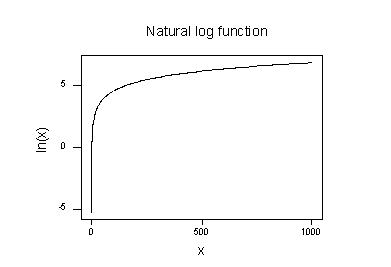
legt nahe, dass die Auswirkungen der natürlichen logarithmischen Transformation sind:
- Kleine Werte, die nahe beieinander liegen, werden weiter ausgebreitet.
- Große Werte, die verteilt sind, werden näher zusammengebracht.
Zurück zum Beispiel. Verwenden wir den natürlichen Logarithmus, um die x-Werte in den Experimentdaten zur Speichererhaltung zu transformieren. Da x = Zeit der Prädiktor ist, müssen wir nur den natürlichen Logarithmus jedes Zeitwerts verwenden, der im Datensatz erscheint. Dabei erstellen wir einen neu transformierten Prädiktor namens lntime:
| time | prop | lntime |
| 1 | 0,84 | 0.00000 |
| 5 | 0.71 | 1.60944 |
| 15 | 0.61 | 2.70805 |
| 30 | 0.56 | 3.40120 |
| 60 | 0.54 | 4.09434 |
| 120 | 0.47 | 4.78749 |
| 240 | 0.45 | 5.48064 |
| 480 | 0.38 | 6.17379 |
| 720 | 0.36 | 6.57925 |
| 1440 | 0.26 | 7.27240 |
| 2880 | 0.20 | 7.96555 |
| 5760 | 0.16 | 8.65869 |
| 10080 | 0.08 | 9.21831 |
We take the natural logarithm for each value of time and place the results in their own column. Das heißt, wir „transformieren“ jeden Prädiktorzeitwert in einen ln (Zeit) -Wert. Zum Beispiel ist ln (1) = 0, ln (5) = 1,60944 und ln (15) = 2,70805 und so weiter.
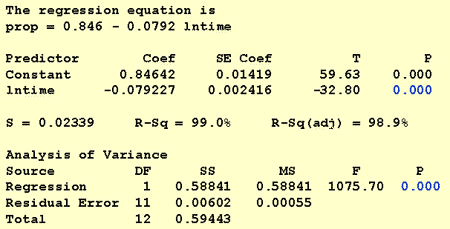
Nachdem wir nun die Prädiktorwerte transformiert haben, wollen wir sehen, ob dies dazu beigetragen hat, den nichtlinearen Trend in den Daten zu korrigieren. Wir passen das Modell mit y = prop als Antwort und x = lntime als Prädiktor neu an.
Das resultierende angepasste Liniendiagramm legt nahe, dass die Verwendung des natürlichen Logarithmus der Prädiktorwerte hilfreich ist.
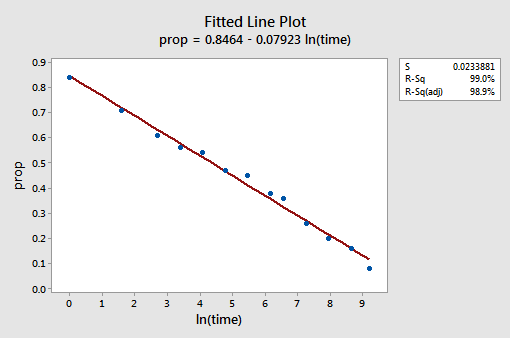
Tatsächlich ist der R2-Wert von 57,1% auf 99,0% gestiegen. Es sagt uns, dass 99% der Variation des Anteils der zurückgerufenen Wörter (prop) durch Berücksichtigung des natürlichen Zeitprotokolls (lntime) reduziert wird!
Das neue Residual-vs. Fits-Diagramm zeigt eine signifikante Verbesserung gegenüber dem Diagramm, das auf den nicht transformierten Daten basiert.
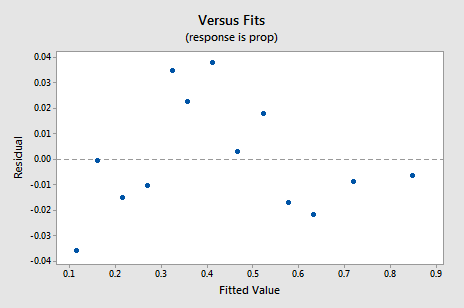
Sie könnten sich Sorgen über eine Art zyklischen Auf-Ab-Trend im Diagramm machen. Ich warne Sie erneut, diese Diagramme nicht zu überinterpretieren, insbesondere wenn der Datensatz so klein ist. Sie sollten wirklich keine Perfektion erwarten, wenn Sie auf Datentransformationen zurückgreifen. Manchmal muss man sich einfach mit signifikanten Verbesserungen zufrieden geben. Übrigens legt das Diagramm auch nahe, dass es in Ordnung ist anzunehmen, dass die Fehlervarianzen gleich sind.
Das Normalwahrscheinlichkeitsdiagramm der Residuen zeigt, dass die Transformation der x-Werte keinen Einfluss auf die Normalität der Fehlerterme hatte:
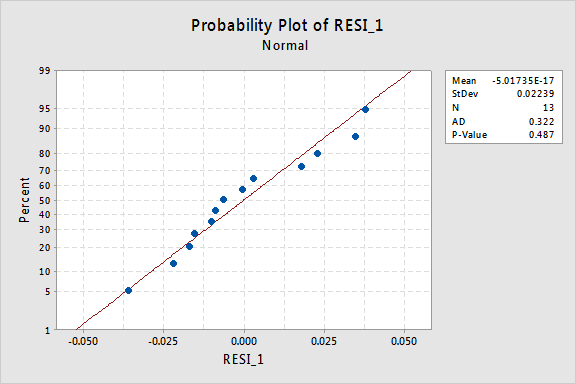
Auch hier ist der Anderson-Darling-P-Wert groß, so dass wir die Nullhypothese normaler Fehlerterme nicht ablehnen können. Es gibt nicht genügend Beweise, um zu dem Schluss zu kommen, dass die Fehlerbedingungen nicht normal sind.
Was wäre, wenn wir stattdessen die y-Werte transformiert hätten? Vorhin habe ich gesagt, dass einige Annahmen vor dem Anwenden einer Transformation zu gelten scheinen, sie jedoch nach dem Anwenden einer Transformation möglicherweise nicht mehr gelten. Wenn sich die Fehlerterme beispielsweise gut verhalten, können sie durch Transformieren der y-Werte in Fehlerterme mit schlechtem Verhalten umgewandelt werden. Die Fehlerterme für die Speichererhaltungsdaten vor der Transformation der x-Werte scheinen sich gut zu verhalten (in dem Sinne, dass sie ungefähr normal erscheinen). Daher können wir erwarten, dass die Transformation der y-Werte anstelle der x-Werte dazu führen kann, dass sich die Fehlerterme schlecht verhalten. Werfen wir einen kurzen Blick auf die Daten zur Speichererhaltung, um ein Beispiel dafür zu sehen, was passieren kann, wenn wir die y-Werte transformieren, wenn Nichtlinearität das einzige Problem ist.
Durch Versuch und Irrtum entdecken wir, dass die Potenztransformation von y, die die Nichtlinearität am besten korrigiert, y-1,25 ist. Das angepasste Liniendiagramm zeigt, dass die Transformation die Beziehung tatsächlich glättet — wenn auch zugegebenermaßen nicht so gut wie die Log-Transformation der x-Werte.
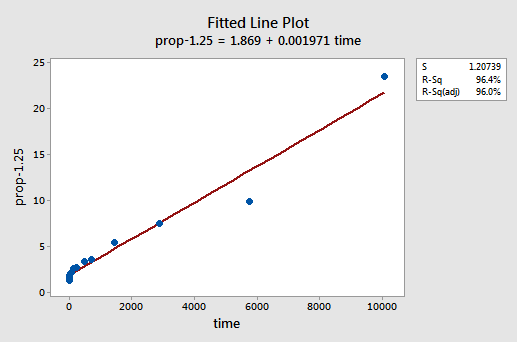
Beachten Sie, dass der R2-Wert von 57,1% auf 96,4% gestiegen ist.
Die Residuen zeigen eine Verbesserung in Bezug auf die Nichtlinearität, obwohl die Verbesserung nicht groß ist…
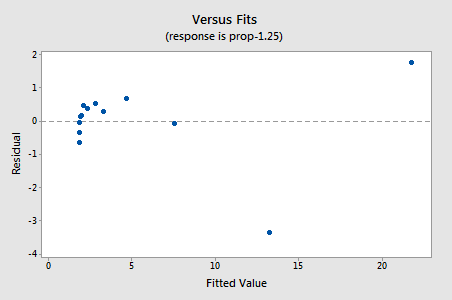
…aber jetzt haben wir nicht normale Fehlerbedingungen! Der Anderson-Darling-P-Wert ist kleiner als 0,005, daher lehnen wir die Nullhypothese normaler Fehlerterme ab. Es gibt genügend Beweise, um zu dem Schluss zu kommen, dass die Fehlerterme nicht normal sind:
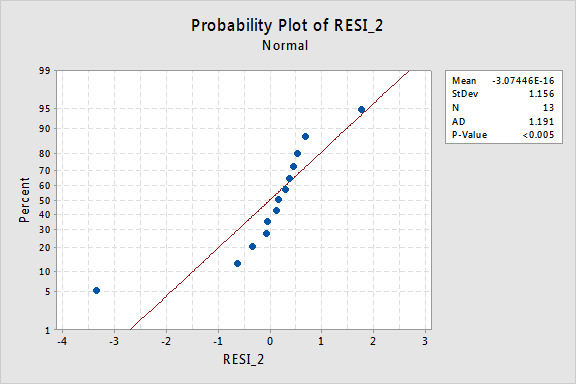
Wenn sich die Fehlerterme vor der Transformation gut verhalten haben, kann die Transformation der y-Werte sie wiederum in schlecht erzogene Fehlerterme verwandeln.
Verwendung des Modells
Sobald wir das beste Modell für unsere Regressionsdaten gefunden haben, können wir das Modell verwenden, um unsere Forschungsfragen von Interesse zu beantworten. Wenn unser Modell transformierte Prädiktorwerte (x) enthält, müssen wir möglicherweise geringfügige Änderungen an den bereits erlernten Standardverfahren vornehmen.
Verwenden wir unser lineares Regressionsmodell für die Daten zur Speichererhaltung — mit y = prop als Antwort und x = lntime als Prädiktor —, um vier verschiedene Forschungsfragen zu beantworten.
Forschungsfrage #1: Was ist die Art der Assoziation zwischen der Zeit seit dem Auswendiglernen und der Wirksamkeit des Rückrufs?
Um diese Forschungsfrage zu beantworten, beschreiben wir nur die Art der Beziehung. Das heißt, der Anteil der korrekt abgerufenen Wörter hängt negativ linear mit dem natürlichen Protokoll der Zeit zusammen, seit die Wörter gespeichert wurden. Es überrascht nicht, dass mit zunehmendem natürlichen Zeitprotokoll der Anteil der zurückgerufenen Wörter abnimmt.Forschungsfrage 2: Gibt es einen Zusammenhang zwischen der Zeit seit dem Auswendiglernen und der Wirksamkeit des Rückrufs?
Bei der Beantwortung dieser Forschungsfrage ist keine Änderung des Standardverfahrens erforderlich. Wir testen lediglich die Nullhypothese H0: β1 = 0 entweder mit dem F-Test oder dem äquivalenten t-Test:
Wie die Softwareausgabe veranschaulicht, ist der P-Wert < 0,001. Es gibt erhebliche Beweise an der 0.05 Ebene zu dem Schluss, dass es eine lineare Assoziation zwischen dem Anteil der zurückgerufenen Wörter und dem natürlichen Protokoll der Zeit seit dem Auswendiglernen gibt.Forschungsfrage #3: Welchen Anteil an Wörtern können wir erwarten, dass sich eine zufällig ausgewählte Person nach 1000 Minuten daran erinnert?
Wir müssen nur ein Vorhersageintervall berechnen — mit einer leichten Modifikation — um diese Forschungsfrage zu beantworten. Unsere Prädiktorvariable ist das natürliche Protokoll der Zeit. Wenn wir statistische Software verwenden, um das Vorhersageintervall zu berechnen, müssen wir daher sicherstellen, dass wir den Wert der Prädiktorwerte in den transformierten Einheiten angeben, nicht in den ursprünglichen Einheiten. Das natürliche Protokoll von 1000 Minuten beträgt 6,91 Protokollminuten. Wenn wir Software verwenden, um ein 95% -Vorhersageintervall zu berechnen, wenn lntime = 6.91 ist, erhalten wir:
Die Ausgabe sagt uns, dass wir zu 95% sicher sein können, dass nach 1000 Minuten eine zufällig ausgewählte person wird zwischen 24,5% und 35 erinnern.3% der Wörter.Forschungsfrage #4: Wie stark verändert sich der erwartete Rückruf, wenn sich die Zeit verzehnfacht?
Wenn Sie darüber nachdenken, bedeutet die Beantwortung dieser Forschungsfrage lediglich die Schätzung und Interpretation des Steigungsparameters β1. Nun, nicht ganz— es gibt eine leichte Anpassung. Im Allgemeinen ist eine k-fache Erhöhung des Prädiktors x mit a verbunden:
β1 × ln(k)
Änderung des Mittelwerts der Antwort y.
Diese folgende Ableitung kann Ihnen helfen, diese Formel zu verstehen und sich daher daran zu erinnern.
Das heißt, ein zehnfacher Anstieg von x ist mit einer β1 × ln (10) -Änderung des Mittelwerts von y verbunden. Und ein zweifacher Anstieg von x ist mit einer β1 × ln(2) -Änderung des Mittelwerts von y verbunden.
Im Allgemeinen sollten Sie nur Vielfache von k verwenden, die für den Umfang des Modells sinnvoll sind. Wenn die x-Werte in Ihrem Datensatz beispielsweise zwischen 2 und 8 liegen, ist es nur sinnvoll, k-Vielfache zu berücksichtigen, die 4 oder kleiner sind. Wenn der Wert von x 2 wäre, würde eine zehnfache Erhöhung (dh k = 10) Sie von 2 auf 2 × 10 = 20 bringen, ein Wert außerhalb des Geltungsbereichs des Modells. Im Datensatz zur Speichererhaltung reichen die Prädiktorwerte von 1 bis 10080, so dass es kein Problem gibt, eine zehnfache Erhöhung in Betracht zu ziehen.
Wenn wir nur an einer Punktschätzung interessiert sind, nehmen wir einfach die Schätzung des Steigungsparameters (b1 = -0,079227) aus der Softwareausgabe:

und multiplizieren sie mit ln(10):
b1 × ln(10) = -0.079227 × ln(10) = -0.182
Wir erwarten, dass der Prozentsatz der zurückgerufenen Wörter abnimmt (da das Vorzeichen negativ ist) 18.2% für jede Verzehnfachung der Zeit seit dem Auswendiglernen.
Natürlich ist diese Punktschätzung von begrenztem Nutzen. Wie sicher können wir sein, dass die Schätzung nahe am wahren unbekannten Wert liegt? Natürlich sollten wir ein Zeitintervall von 95% berechnen. Dazu berechnen wir einfach ein 95% -Konfidenzintervall für β1, wie wir es immer haben: