Escaleno triángulo es un triángulo con todos los lados de longitudes diferentes.
Todos los ángulos también son diferentes.
Por lo tanto, ningún lado es igual y ningún ángulo es igual.
Fórmula para el Área del Triángulo Escaleno :
= √
donde
S = (a + b + c) / 2
Aquí a, b y c son las longitudes de los lados del triángulo.
Problemas de práctica
Problema 1:
Encuentre el área del triángulo escaleno cuya longitud de lados sea de 12 cm, 18 cm y 20 cm.
Solución :
Debido a que las longitudes de los tres lados son diferentes, el triángulo es escaleno.
S = (a + b + c) / 2
Substitute 12 for a, 18 for b and 20 for c.
S = (12 + 18 + 20) / 2
S = 50/2
S = 25
Formula for area of scalene triangle :
= √
Substitute.
= √
= √(25 x 13 x 7 x 5)
= 5√455
Así, área del triángulo escaleno es de 5 √455 cm cuadrados.
Problema 2 :
Los lados de un triángulo escaleno son de 12 cm, 16 cm y 20 cm. Encuentra la altitud hasta el lado más largo.
Solución :
con el fin De encontrar la altitud para el lado más largo de un triángulo, primero tenemos que hallar el área del triángulo.
S = (a + b + c) / 2
Substitute 12 for a, 16 for b and 20 for c.
S = (12 + 16 + 20) / 2
S = 48/2
S = 24
Formula for area of scalene triangle :
= √
Substitute.
= √
= √(24 x 12 x 8 x 4)
= 96 cm2
Porque queremos encontrar la altitud para el lado más largo, el lado más largo será la base del triángulo, como se muestra a continuación.
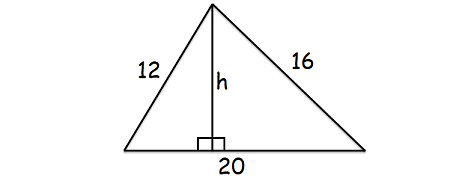
Aquí, el lado más largo es de 20 cm.
Área de las anteriores triángulo = 96 cm2
(1/2) x 20 x h = 96
10h = 96
Dividir cada lado por 10.
h = 9,6 cm
Por lo tanto, la altitud hasta el lado más largo es de 9,6 cm.
Problema 3 :
Los lados de un triángulo escaleno están en la relación (1/2) : (1/3) : (1/4). Si el perímetro es de 52 cm, busque la longitud del lado más pequeño.
Solución :
From the given information, the sides the triangle are
x/2, x/3 and x/4
Perimeter of the triangle = 52 cm
(x/2) + (x/3) + (x/4) = 52
(6x + 4x + 3x) / 12 = 52
13x / 12 = 52
13x = 624
x = 48
Then,
x/2 = 24
x/3 = 16
x/4 = 12
So, the length del lado más pequeño es de 12 cm.
Problema 4:
El área del triángulo escaleno es de 216 cm2 y los lados están en una proporción de 3: 4: 5. Encuentra el perímetro del triángulo.
Solución :
From the given information, the sides the triangle are
3x, 4x and 5x
S = (3x + 4x + 5x) / 2
S = 6x
Area of the triangle = 216 cm2
√ = 216
√ = 216
√ = 216
√(36×4) = 216
6×2 = 216
x2 = 36
x = 6
Then,
3x = 18
4x = 24
5x = 30
el Perímetro del triángulo escaleno es
= 18 + 24 + 30
= 72 cm
Problema 5 :
Uno de los lados de un ángulo recto triángulo escaleno es el doble de la otra,y la hipotenusa es 10 cm. Encuentra el área del triángulo.
Solución:
Sea ‘x’ la longitud de una de las patas del triángulo.
Entonces, la longitud de la otra pierna es 2x.
Using Pythagorean theorem,
x2 + (2x)2 = 102
x2 + 4×2 = 100
5×2 = 100
x2 = 20
√x2 = √20
x = √(4 x 5)
x = 2√5
Then,
2x = 2(2√5)
2x = 4√5
Area of the given right angle scalene triangle is
= (1/2)(x) (2x)
= (1/2)(2√5)(4√5)
= 20 cm2

Aparte de las cosas de arriba, si usted necesita cualquier otra cosa en matemáticas, por favor, utilice nuestra búsqueda personalizada de google aquí.
Si tiene algún comentario sobre nuestro contenido matemático, envíenos un correo electrónico a:
Siempre agradecemos sus comentarios.
También puede visitar las siguientes páginas web sobre diferentes temas de matemáticas.
PROBLEMAS VERBALES
Problemas verbales HCF y LCM
Problemas verbales en ecuaciones simples
Problemas verbales en ecuaciones lineales
Problemas verbales en ecuaciones cuadráticas
Problemas verbales de álgebra
Problemas verbales en trenes
Problemas verbales de área y perímetro
Problemas verbales de variación directa e inversa
Problemas verbales de precio unitario
Problemas verbales de tasa unitaria
Problemas verbales de comparación de tasas
Problemas verbales de conversión de unidades habituales
Conversión de unidades métricas de palabras problemas
Problemas verbales de interés simple
Problemas verbales de interés compuesto
Problemas verbales de tipos de ángulos
Problemas verbales de ángulos complementarios y suplementarios
Problemas verbales de hechos dobles
Problemas verbales de trigonometría
Problemas verbales de porcentaje
Problemas verbales de pérdidas y ganancias
problemas verbales de rebaja
Problemas verbales decimales
Problemas verbales en fracciones
Problemas verbales en fractriones mixtos
Problemas verbales de ecuación de un paso
Problemas verbales de desigualdades lineales
Relación y problemas verbales de proporción
Problemas verbales de tiempo y trabajo
Problemas verbales en conjuntos y diagramas de venn
Problemas verbales en edades
Teorema de pitágoras problemas verbales
Porcentaje de un número problemas verbales
Problemas verbales en velocidad constante
Problemas verbales en velocidad media
Problemas verbales en la suma de los ángulos de un triángulo es de 180 grados
OTROS TEMAS
Atajos de pérdidas y ganancias
Atajos de porcentaje
Atajos de tabla de tiempos
Atajos de tiempo, velocidad y distancia
Atajos de proporción y proporción
Dominio y rango de funciones racionales
Dominio y rango de funciones racionales con agujeros
Graficar funciones racionales
Graficar funciones racionales con agujeros
Convertir decimales repetidos en fracciones
Representación decimal de números racionales
Encontrar raíz cuadrada usando división larga
L. C.Método M para resolver problemas de tiempo y trabajo
Traducir los problemas verbales a expresiones algebraicas
Resto cuando 2 potencias 256 se dividen por 17
Resto cuando 17 potencias 23 se dividen por 16
Suma de los tres números divisibles por 6
Suma de los tres números divisibles por 7
Suma de todos los números de tres dígitos divisibles por 8
Suma de todos los números de tres dígitos formados con 1, 3, 4
Suma de los tres números de cuatro dígitos formados con dígitos distintos de cero
Suma de los tres números de cuatro dígitos formados con 0, 1, 2, 3
Suma de los tres números de cuatro dígitos formados con 1, 2, 5, 6