3.3 El Ciclo de Carnot | Maybaygiare.org

Siguiente: 3.4 Refrigerador y Calor Arriba: 3. La Primera Ley Anterior: 3.2 Representación Generalizada del Índice de Contenidos

Un ciclo de Carnot se muestra en la Figura 3.4. Tiene cuatro procesos. Hay dos patas reversibles adiabáticas y dos patas reversibles térmicas. Podemos construir un ciclo de Carnot con muchos sistemas diferentes, pero los conceptos se pueden mostrar utilizando un fluido de trabajo familiar, el gas ideal. El sistema puede considerarse como una cámara encerrada por un pistón y llena con este gas ideal.

Figura 3.4: Ciclo de Carnot diagram diagrama termodinámico a la izquierda y esquema de las diferentes etapas del ciclo para un sistema compuesto de un gas ideal a la derecha

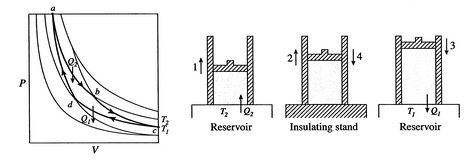
Los cuatro procesos en el ciclo de Carnot son:

El sistema está a temperatura 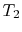en el estado . Se produce en contacto con un depósito de calor, que es solo una masa líquida o sólida de una extensión lo suficientemente grande como para que su temperatura no cambie apreciablemente cuando se transfiere cierta cantidad de calor al sistema. En otras palabras, el depósito de calor es una fuente de temperatura constante (o receptor) de calor. A continuación, el sistema se somete a anisothermal expansión de a , con el calor absorbido .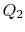
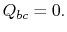Atstate , el sistema está aislado térmicamente (se elimina del contacto con el depósito de calor) y luego se deja expandir a . Durante esta expansión, la temperatura disminuye a . El intercambiador de calor durante esta parte del ciclo, $Q Q_{bc} = 0.$$ )
En el estado el sistema está en contacto con un depósito de calor a temperatura . Es isthen comprimido a estado 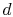, rechazando calor 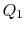en el proceso.
Finalmente, el sistema se comprime adiabáticamente de nuevo al estado inicial . El intercambio de calor $Q_{da}=0$ .

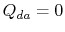La eficiencia térmica del ciclo está dado por la definición

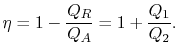$\displaystyle \eta = 1 - \frac{Q_R}{Q_A}=1+\frac{Q_1}{Q_2}.$

(3..4)

En esta ecuación, hay una convención de signos implícita. Las cantidades como se define son las magnitudes del calor absorbido andrejected. Las cantidades en el otro lado están definedwith referencia al calor recibido por el sistema. En este ejemplo, elformador es negativo y el segundo es positivo. El calor absorbido y proyectado por el sistema tiene lugar durante los procesos isotérmicos y ya sabemos cuáles son sus valores a partir de la Ec.(3.1):

$\displaystyle Q_2 = W_{ab} =N\mathbf{R}T_2 ,$

$$\displaystyle Q_1 = W_{cd} =N\mathbf{R}T_1 =-N\mathbf{R}T_1 .\quad \ textrm {(Q Q_1 is es negativo.)}$

La eficiencia ahora se puede escribir en términos de volúmenes en los diferentes estados como

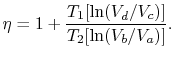$\\displaystyle \eta = 1+ \ frac{T_1}{T_2}.$$

(3..5)

The path from states to and from to are bothadiabatic and reversible. For a reversible adiabatic process we knowthat $PV^\gamma= \textrm{constant}$ . Using the ideal gas equation ofstate, we have $T V^{\gamma-1} = \textrm{constant}$ . Along curve, therefore, $T_2 V_b^{\gamma-1}=T_1 V_c^{\gamma-1}$ . Alongthe curve $T_2 V_a^{\gamma-1}=T_1 V_d^{\gamma-1}$ . Thus,

$\displaystyle \left(\frac{V_d}{V_c}\right)^{\gamma-1} =\frac{(T_2/T_1)}{(T_2/T......right)^{\gamma-1},\textrm{ whichmeans that } \frac{V_d}{V_c}=\frac{V_a}{V_b}.$

Comparing the expression for thermal efficiencyEq. (3.4) with Eq. (3.5) muestra dos consecuencias. En primer lugar, los calores recibidos y rechazados se relacionan con las temperaturas de las partes isotérmicas del ciclo por

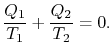$\\displaystyle\frac{Q_1}{T_1}+ \ frac{Q_2}{T_2}= 0.$$

(3..6)

en Segundo lugar, la eficiencia de un ciclo de Carnot se da de forma compacta por

$$\displaystyle \eta = 1 - \frac{T_1}{T_2}.\qquad\textbf{Eficiencia del ciclo de Carnot.}}$

(3..7)

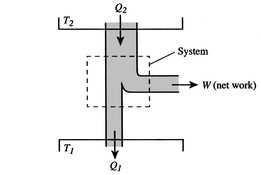
La eficiencia puede ser del 100% solo si la temperatura a la que se rechaza el calor es cero. Las transferencias de calor y trabajo hacia y desde el sistema se muestran esquemáticamente en la figura 3.5.

Figura 3.5:El trabajo y las transferencias de calor ina ciclo de Carnot entre dos reservorios de calor

Barro Puntos

Desde $\eta = 1- {T_1}/{T_2}$ , busca en la etiqueta gráfico, doesthat significa el más separados, el isotermas son, thegreater eficiencia? Y que si estaban muy cerca, sería muy ineficiente? (MP 3.2)