Experiencia: Intermedio
¿Qué es una función spline?Necesitamos saber cuáles son las características esenciales de las tablillas antes de considerar cómo construir un sistema de base para ellas.Las funciones Spline se forman uniendo polinomios en puntos fijos llamados nudos. Es decir, dividimos el intervalo que se extiende desde el límite inferior TL límite toupper tU sobre el que deseamos aproximar una curva en L+1 sub-intervalos separados por L límites interiores ξl llamados nudos, o a veces puntos de interrupción.Hay una distinción entre estos dos términos, pero llegaremos a esto más adelante.Considere el caso más simple en el que un único punto de interrupción divide el intervalo en dos subintervalos. La función férula es, dentro de cada intervalo, un polinomio de grado especificado(la potencia más alta que define el polinomio) u orden (el número de coeficientes que definen el polinomio, que es uno más que su grado). Usemos m para designar el orden del polinomio, de modo que el grado sea m – 1:
En el punto de interrupción interior ξ1, se requiere que los dos polinomios se unan sin problemas. En el caso más común, esto significa que las derivadas coinciden hasta el orden uno menos que el grado. De hecho, si coinciden con la derivada cuyo orden iguala el grado, serían el mismo polinomio. Por lo tanto, una función estriada definida en este was tiene un grado de libertad adicional que un polinomio que se extiende sobre todo el intervalo.
Por ejemplo, deje que cada polinomio sea un segmento de línea recta, y por lo tanto de grado uno. En esto, se unen en el punto de interrupción con derivados coincidentes hasta el grado 0; en resumen, simplemente se unen y tienen valores idénticos en el punto de interrupción. Dado que el primer polinomio tiene dos grados de libertad (pendiente e intersección), y el segundo, que tiene su valor ya definido en el punto de ruptura,queda con un solo grado de libertad (pendiente), la línea poligonal total tiene tres grados de libertad.
Correspondientemente, si ambos polinomios son cuadráticos, entonces la coincidencia en términos de valores y en términos de pendiente del primer derivado en ξ1. El primer polinomio tiene tres grados de libertad, pero el segundo pierde dos porque si la restricción en su valor y pendiente en ξi, y por lo tanto retiene solo uno. Esto deja un total de cuatro grados de libertad para la función de férula formada de esta manera, como opuesto a tres para un polinomio cuadrático durante todo el intervalo. La Figura 1 muestra los casos lineales y cuadráticos con un único punto de interrupción.
¿Cuáles son algunos ejemplos de funciones básicas de uso común?Ahora podemos generalizar la situación a L puntos de interrupción interiores, y una función de spline de orden m o grado m-1 en cada intervalo sub. El primer segmento polinómico tiene un complemento completo de m grados de libertad, pero cada segmento subsiguiente solo tiene un grado de libertad debido a las restricciones m – 1 en su comportamiento.Esto da un total de L + m grados de libertad, o número de puntos de ruptura interiores más el orden de los segmentos polinómicos.
Por lo tanto, las funciones spline son esencialmente generalizaciones de la noción de poligonalinas. Obtienen su flexibilidad de dos maneras: En primer lugar, por el orden de los polinomios a partir de los cuales se construyen, y en segundo lugar, por el número de puntos de ruptura utilizados. Por lo general, elegimos mantener el orden fijo y agregar puntos de interrupción según sea necesario para obtener la flexibilidad requerida.
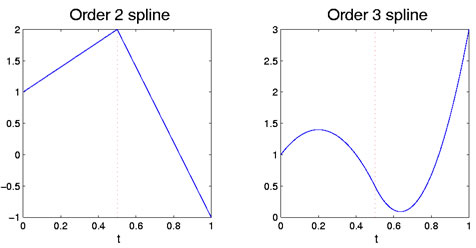
Figura 1: La figura de la izquierda muestra una función de orden de dos estrías, que es lineal por partes. La figura derecha es una estría de orden 3, que es cuadrática por partes. El punto de ruptura en 0,5 se indica con la línea de puntos vertical roja.