Definición
Un polinomio en la variable x es una función que puede ser escrita en la forma,
donde an, an-1 , …, a2, a1, a0 son constantes. Llamamos al término que contiene la potencia más alta de x (es decir, anxn) el término principal, y llamamos a un coeficiente principal. El grado del polinomio es la potencia de x en el término principal. Ya hemos visto polinomios de grado 0, 1 y 2 que eran las funciones constantes, lineales y cuadráticas, respectivamente. Los polinomios de grado 3, 4 y 5 también tienen nombres especiales: funciones cúbicas, cuarticas y quinticas. Los polinomios con grado n > 5 se denominan polinomios de enésimo grado. Los nombres de las diferentes funciones polinómicas se resumen en la siguiente tabla.
| Degree of the polynomial | Name of the function |
| 0 | Constant function |
| 1 | Linear function |
| 2 | Quadratic function |
| 3 | Cubic function |
| 4 | Quartic function |
| 5 | Quintic Function |
| n (where n > 5) | nth degree polynomial |
Some examples of polynomials include:
El comportamiento Limitante de Polinomios
El comportamiento limitante de una función describe lo que le sucede a la función como x → ±∞. El grado de un polinomio y el signo de su coeficiente principal dictan su comportamiento limitante. En particular,
Estos resultados se resumen en el cuadro que figura a continuación.
Puede usar esta información para determinar si un polinomio tiene grado impar o par y si el coeficiente principal es positivo o negativo, simplemente inspeccionando su gráfico.
Los siguientes gráficos de polinomios ejemplifican cada uno de los comportamientos descritos en la tabla anterior.
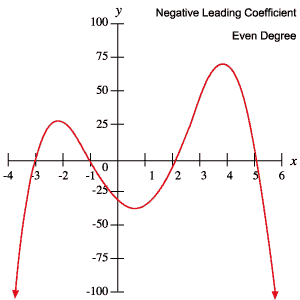
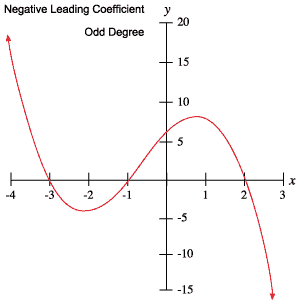
las Raíces y los Puntos de Inflexión
El grado de un polinomio se dice que incluso más que el comportamiento limitante. Específicamente, un polinomio de enésimo grado puede tener como máximo n raíces reales (x-interceptas o ceros) contando multiplicidades. Por ejemplo, supongamos que estamos viendo un polinomio de 6º grado que tiene 4 raíces distintas. Si dos de las cuatro raíces tienen multiplicidad 2 y las otras 2 tienen multiplicidad 1, sabemos que no hay otras raíces porque hemos tenido en cuenta las 6 raíces. Esto se debe a que las raíces con una multiplicidad de dos (también conocidas como raíces dobles) se cuentan como dos raíces.
Tenga en cuenta que un polinomio de enésimo grado no necesita tener n raíces reales, podría tener menos porque tiene raíces imaginarias. Observe que un polinomio de grado impar debe tener al menos una raíz real, ya que la función se aproxima a – ∞ en un extremo y a + ∞ en el otro; una función continua que cambia de negativo a positivo debe intersecar el eje x en algún lugar intermedio. Además, un polinomio de enésimo grado puede tener como máximo n-1 puntos de inflexión. Un punto de inflexión es un punto en el que la función cambia de aumentar a disminuir o disminuir a aumentar como se ve en la figura a continuación. Una vez más, un polinomio de enésimo grado no necesita tener n – 1 puntos de inflexión, podría tener menos.
Nota de Precaución
es importante darse cuenta de la diferencia entre par e impar y funciones pares e impares de grado de los polinomios. Cualquier función, f(x), es incluso si,
f(−x) = x,
para todo x en el dominio de f(x), o impar si,
f(−x) = −x,
para todo x en el dominio de f(x), o ni siquiera ni impar si ninguno de los anteriores son verdaderas declaraciones.
Se dice que un polinomio de grado k, p(x), tiene grado par si k es un número par y grado impar si k es un número impar. Recuerde que incluso si p (x) tiene un grado par, no es necesariamente una función par. Del mismo modo, si p(x) tiene grado impar, no es necesariamente una función impar.
También usamos los términos par e impar para describir raíces de polinomios. Específicamente, un polinomio p(x) tiene raíz x = a de multiplicidad k (es decir, x = a es una raíz repetido k veces) si (x − a)k es un factor de p(x). Decimos que x = a tiene incluso multiplicidad si k es un número par y multiplicidad impar si k es un número impar.
Dominio y rango
Todos los polinomios tienen el mismo dominio que consiste en todos los números reales. El rango de polinomios de grado impar también consiste en todos los números reales. El rango de polinomios de grado par es un poco más complicado y no podemos declarar explícitamente el rango de todos los polinomios de grado par. Si el coeficiente principal es positivo, la función se extenderá a + ∞; mientras que si el coeficiente principal es negativo, se extenderá a – ∞. Esto significa que los polinomios de grado uniforme con coeficiente inicial positivo tienen un rango donde ymax denota el máximo global que alcanza la función. En general, no es posible determinar analíticamente los máximos o mínimos de polinomios.
*****
En la siguiente sección aprenderás la división polinómica, una técnica utilizada para encontrar las raíces de las funciones polinómicas.
División polinómica