Comprender la regresión logística en Python

Las técnicas de clasificación son una parte esencial de las aplicaciones de aprendizaje automático y minería de datos. Aproximadamente el 70% de los problemas en la ciencia de datos son problemas de clasificación. Hay muchos problemas de clasificación disponibles, pero la regresión logística es común y es un método de regresión útil para resolver el problema de clasificación binaria. Otra categoría de clasificación es la clasificación multinomial, que maneja los problemas en los que hay varias clases presentes en la variable de destino. Por ejemplo, el conjunto de datos IRIS es un ejemplo muy famoso de clasificación de varias clases. Otros ejemplos son la clasificación de categoría de artículo / blog / documento.

La regresión logística se puede utilizar para varios problemas de clasificación, como la detección de spam. Predicción de diabetes, si un cliente determinado comprará un producto en particular o eliminará a otro competidor, si el usuario hará clic en un enlace de anuncio determinado o no, y muchos más ejemplos están en el cubo.

La regresión logística es uno de los algoritmos de aprendizaje automático más simples y comúnmente utilizados para la clasificación de dos clases. Es fácil de implementar y se puede usar como base para cualquier problema de clasificación binaria. Sus conceptos fundamentales básicos también son constructivos en el aprendizaje profundo. La regresión logística describe y estima la relación entre una variable binaria dependiente y variables independientes.

En este tutorial, aprenderá las siguientes cosas en Regresión Logística:

• Introducción a la Regresión Logística
• Regresión Lineal Vs. Regresión Logística
• Estimación de Máxima Verosimilitud Vs. Método Ordinario de Mínimos Cuadrados
• ¿Cómo funciona la Regresión Logística?
• Creación de modelos en Scikit-aprenda
• Evaluación de modelos utilizando la Matriz de Confusión.
• Ventajas y desventajas de la Regresión Logística

Regresión Logística

La regresión logística es un método estadístico para predecir clases binarias. La variable de resultado o meta es de naturaleza dicotómica. Dicotómico significa que solo hay dos clases posibles. Por ejemplo, se puede usar para problemas de detección de cáncer. Calcula la probabilidad de que ocurra un evento.

Es un caso especial de regresión lineal donde la variable objetivo es de naturaleza categórica. Utiliza un registro de probabilidades como variable dependiente. Logistic Regression predicts the probability of occurrence of a binary event utilizing a logit function.

Linear Regression Equation:

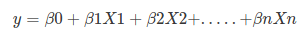
Where, y is dependent variable and x1, x2 … and Xn are explanatory variables.

Sigmoid Function:

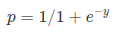
Apply Sigmoid function on linear regression:

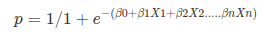
Properties of Logistic Regression:

• La variable dependiente en regresión logística sigue la distribución de Bernoulli.
• La estimación se realiza a través de la máxima verosimilitud.
• Sin R Cuadrado, la aptitud del modelo se calcula a través de la Concordancia, Estadísticas KS.

Regresión lineal Vs. Regresión logística

La regresión lineal le da una salida continua, pero la regresión logística proporciona una salida constante. Un ejemplo de la producción continua es el precio de la vivienda y el precio de las acciones. El ejemplo de la salida discreta es predecir si un paciente tiene cáncer o no, predecir si el cliente se retirará. La regresión lineal se estima utilizando Mínimos Cuadrados Ordinarios (OLS), mientras que la regresión logística se estima utilizando el enfoque de Estimación de Máxima Verosimilitud (MLE).

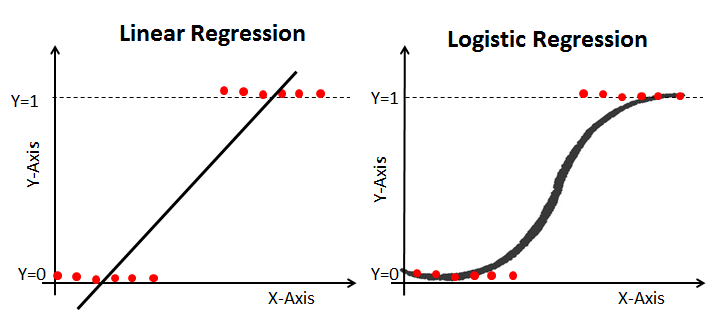
Estimación de máxima Verosimilitud Vs. Método de Mínimos Cuadrados

El MLE es un método de maximización de» verosimilitud», mientras que el OLS es un método de aproximación que minimiza la distancia. La maximización de la función de verosimilitud determina los parámetros que tienen más probabilidades de producir los datos observados. Desde un punto de vista estadístico, MLE establece la media y la varianza como parámetros para determinar los valores paramétricos específicos para un modelo dado. Este conjunto de parámetros se puede utilizar para predecir los datos necesarios en una distribución normal.

Las estimaciones de mínimos cuadrados ordinarios se calculan ajustando una línea de regresión en puntos de datos dados que tiene la suma mínima de las desviaciones al cuadrado (error de mínimos cuadrados). Ambos se utilizan para estimar los parámetros de un modelo de regresión lineal. MLE asume una función de masa de probabilidad conjunta, mientras que OLS no requiere suposiciones estocásticas para minimizar la distancia.

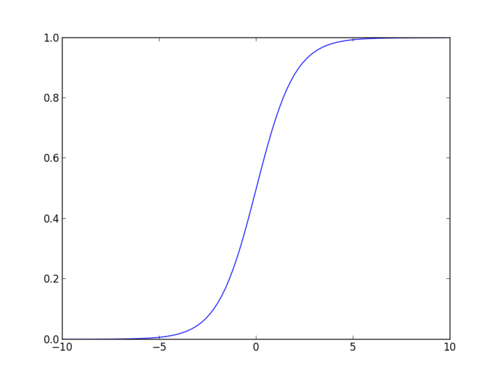
Función sigmoide

La función sigmoide, también llamada función logística, da una curva en forma de » S » que puede tomar cualquier número de valor real y asignarlo a un valor entre 0 y 1. Si la curva va a infinito positivo, y predicho se convertirá en 1, y si la curva va a infinito negativo, y predicho se convertirá en 0. Si la salida de la función sigmoide es superior a 0,5, podemos clasificar el resultado como 1 o SÍ, y si es inferior a 0.5, podemos clasificarlo como 0 o NO. El resultado No puede por ejemplo: Si el resultado es de 0,75, podemos decir en términos de probabilidad como: Hay un 75 por ciento de probabilidades de que el paciente sufra cáncer.

Tipos de Regresión Logística

Tipos de Regresión Logística:

• Regresión Logística Binaria: La variable tiene sólo dos resultados posibles, tales como Spam o No Spam, Cáncer o No Cáncer.
• Regresión Logística Multinomial: La variable objetivo tiene tres o más categorías nominales, como predecir el tipo de Vino.
• Regresión Logística Ordinal: la variable objetivo tiene tres o más categorías ordinales, como la clasificación de restaurantes o productos de 1 a 5.

Creación de modelos en Scikit-aprenda

Construyamos el modelo de predicción de diabetes.

Aquí, va a predecir la diabetes utilizando el Clasificador de Regresión Logística.

Primero carguemos el conjunto de datos de Diabetes India Pima requerido usando la función CSV de lectura de pandas. Usted puede descargar los datos desde el siguiente enlace: https://www.kaggle.com/uciml/pima-indians-diabetes-database

los Datos de Carga

#import pandasimport pandas as pdcol_names = # load datasetpima = pd.read_csv("pima-indians-diabetes.csv", header=None, names=col_names)

pima.head()

Selección de Función

Aquí, es necesario dividir el dado columnas en dos tipos de variables dependientes(o variable objetivo) y la variable independiente(o función de variables).

#split dataset in features and target variablefeature_cols = X = pima # Featuresy = pima.label # Target variable

Dividir datos

Para comprender el rendimiento del modelo, dividir el conjunto de datos en un conjunto de entrenamiento y un conjunto de pruebas es una buena estrategia.

Dividamos el conjunto de datos usando la función train_test_split (). Debe pasar 3 parámetros, características, destino y tamaño del conjunto de pruebas. Además, puede usar random_state para seleccionar registros de forma aleatoria.

# split X and y into training and testing setsfrom sklearn.cross_validation import train_test_splitX_train,X_test,y_train,y_test=train_test_split(X,y,test_size=0.25,random_state=0)

/home/admin/.local/lib/python3.5/site-packages/sklearn/cross_validation.py:41: DeprecationWarning: This module was deprecated in version 0.18 in favor of the model_selection module into which all the refactored classes and functions are moved. Also, note that the interface of the new CV iterators is different from that of this module. This module will be removed in 0.20. "This module will be removed in 0.20.", DeprecationWarning)

Aquí, el conjunto de datos se divide en dos partes, en una proporción de 75:25. Significa que el 75% de los datos se utilizarán para el entrenamiento de modelos y el 25% para las pruebas de modelos.

Desarrollo y predicción de modelos

Primero, importe el módulo de Regresión Logística y cree un objeto clasificador de Regresión Logística utilizando la función LogisticRegression ().

Luego, ajuste su modelo en el conjunto de trenes usando fit () y realice la predicción en el conjunto de pruebas usando predict ().

# import the classfrom sklearn.linear_model import LogisticRegression# instantiate the model (using the default parameters)logreg = LogisticRegression()# fit the model with datalogreg.fit(X_train,y_train)#y_pred=logreg.predict(X_test)

Evaluación del modelo mediante Matriz de confusión

Una matriz de confusión es una tabla que se utiliza para evaluar el rendimiento de un modelo de clasificación. También puede visualizar el rendimiento de un algoritmo. Lo fundamental de una matriz de confusión es el número de predicciones correctas e incorrectas que se resumen en términos de clase.

# import the metrics classfrom sklearn import metricscnf_matrix = metrics.confusion_matrix(y_test, y_pred)cnf_matrix

array(, ])

Aquí, se puede ver la matriz de confusión en la forma de la matriz objeto. La dimensión de esta matriz es 2*2 porque este modelo es de clasificación binaria. Tienes dos clases 0 y 1. Los valores diagonales representan predicciones precisas, mientras que los elementos no diagonales son predicciones inexactas. En la salida, 119 y 36 son predicciones reales, y 26 y 11 son predicciones incorrectas.

Visualizando la matriz de confusión usando Mapa de calor

Visualicemos los resultados del modelo en forma de una matriz de confusión usando matplotlib y seaborn.

Aquí, visualizará la matriz de confusión usando Mapa de calor.

# import required modulesimport numpy as npimport matplotlib.pyplot as pltimport seaborn as sns%matplotlib inline

class_names= # name of classesfig, ax = plt.subplots()tick_marks = np.arange(len(class_names))plt.xticks(tick_marks, class_names)plt.yticks(tick_marks, class_names)# create heatmapsns.heatmap(pd.DataFrame(cnf_matrix), annot=True, cmap="YlGnBu" ,fmt='g')ax.xaxis.set_label_position("top")plt.tight_layout()plt.title('Confusion matrix', y=1.1)plt.ylabel('Actual label')plt.xlabel('Predicted label')

Text(0.5,257.44,'Predicted label')

Métricas de evaluación de matriz de confusión

Evaluemos el modelo utilizando métricas de evaluación del modelo como precisión, precisión y recuperación.

print("Accuracy:",metrics.accuracy_score(y_test, y_pred))print("Precision:",metrics.precision_score(y_test, y_pred))print("Recall:",metrics.recall_score(y_test, y_pred))

Accuracy: 0.8072916666666666Precision: 0.7659574468085106Recall: 0.5806451612903226

Bueno, tienes una tasa de clasificación del 80%, considerada como buena precisión.

Precisión: La precisión se trata de ser preciso, es decir, cuán preciso es su modelo. En otras palabras, se puede decir, cuando un modelo hace una predicción, con qué frecuencia es correcta. En su caso de predicción, cuando su modelo de Regresión Logística predijo que los pacientes sufrirán diabetes, los pacientes tienen el 76% del tiempo.

Recordar: Si hay pacientes que tienen diabetes en el conjunto de pruebas y su modelo de Regresión Logística puede identificarlo el 58% de las veces.

Curva ROC

La curva de Características de Funcionamiento del receptor(ROC) es una gráfica de la tasa positiva verdadera contra la tasa positiva falsa. Muestra el equilibrio entre sensibilidad y especificidad.

y_pred_proba = logreg.predict_proba(X_test)fpr, tpr, _ = metrics.roc_curve(y_test, y_pred_proba)auc = metrics.roc_auc_score(y_test, y_pred_proba)plt.plot(fpr,tpr,label="data 1, auc="+str(auc))plt.legend(loc=4)plt.show()

AUC puntuación para el caso es de 0,86. La puntuación AUC 1 representa un clasificador perfecto, y 0,5 representa un clasificador sin valor.

Ventajas

Debido a su naturaleza eficiente y directa, no requiere un alto poder de cálculo, fácil de implementar, fácilmente interpretable, utilizado ampliamente por analistas y científicos de datos. Además, no requiere escalado de características. La regresión logística proporciona una puntuación de probabilidad para las observaciones.

Desventajas

La regresión logística no es capaz de manejar un gran número de características/variables categóricas. Es vulnerable al sobreajuste. Además, no puede resolver el problema no lineal con la regresión logística, por eso requiere una transformación de características no lineales. La regresión logística no funcionará bien con variables independientes que no están correlacionadas con la variable objetivo y son muy similares o correlacionadas entre sí.

Conclusión

En este tutorial, cubriste muchos detalles sobre la Regresión logística. Ha aprendido qué es la regresión logística, cómo construir los modelos respectivos, cómo visualizar los resultados y parte de la información de fondo teórica. Además, cubrió algunos conceptos básicos como la función sigmoide, máxima verosimilitud, matriz de confusión, curva ROC.

Con suerte, ahora puede utilizar la técnica de Regresión Logística para analizar sus propios conjuntos de datos. Gracias por leer este tutorial!

Si desea obtener más información sobre la Regresión Logística, tome el curso Fundamentos del Análisis Predictivo en Python de DataCamp (Parte 1).