En astronomía, los tamaños de los objetos celestes a menudo se dan en términos de su diámetro angular visto desde la Tierra, en lugar de sus tamaños reales. Dado que estos diámetros angulares son típicamente pequeños, es común presentarlos en segundos de arco («). Un segundo de arco es 1/3600 de un grado (1°) y un radián es 180/ π {\displaystyle \pi }

grados. Así que un radián es igual a 3.600 × 180/ π {\displaystyle \pi }

segundos de arco, que es aproximadamente 206.265 segundos de arco (1 rad ≈ 206.264, 806247″). Por lo tanto, el diámetro angular de un objeto con diámetro físico d a una distancia D, expresado en segundos de arco, está dado por: δ = 206 , 265 ( d / D ) a r c s e c o n d s {\displaystyle \delta =206,265~(d/D)~\mathrm {segundos de arco} }

.
Estos objetos tienen un diámetro angular de 1″:
- un objeto de diámetro 1 cm a una distancia de 2,06 km
- un objeto de diámetro 725,27 km a una distancia de 1 unidad astronómica (UA)
- un objeto de diámetro 45 866 916 km a 1 año luz
- un objeto de diámetro 1 UA (149 597 871 km) a una distancia de 1 parsec (pc)
, el diámetro angular de la órbita de la Tierra alrededor del Sol visto desde una distancia de 1 PC es de 2″, ya que 1 UA es el radio medio de la órbita de la Tierra.
El diámetro angular del Sol, desde una distancia de un año luz, es de 0,03″, y el de la Tierra de 0,0003″. El diámetro angular 0.03″ del Sol dado arriba es aproximadamente lo mismo que el de un cuerpo humano a una distancia del diámetro de la Tierra.
Esta tabla muestra los tamaños angulares de cuerpos celestes notables vistos desde la Tierra:
| Cuerpo celeste | Diámetro o tamaño angular | Tamaño relativo |
|---|---|---|
| Galaxia de Andrómeda | 3°10′ por 1° | Aproximadamente seis veces el tamaño del Sol o de la Luna. Solo el núcleo mucho más pequeño es visible sin fotografía de larga exposición. |
| Sun | 31′27″ – 32′32″ | 30–31 times the maximum value for Venus (orange bar below) / 1887–1952″ |
| Moon | 29′20″ – 34′6″ | 28–32.5 times the maximum value for Venus (orange bar below) / 1760–2046″ |
| Helix Nebula | about 16′ by 28′ | |
| Spire in Eagle Nebula | 4′40″ | length is 280″ |
| Venus | 9.7″ – 1′6″ | |
| Jupiter | 29.8″ – 50.1″ | |
| Saturn | 14.5″ – 20.1″ | |
| Mars | 3.5″ – 25.1″ | |
| Mercury | 4.5″ – 13.0″ | |
| Uranus | 3.3″ – 4.1″ | |
| Neptune | 2.2″ – 2.4″ | |
| Ceres | 0.33″ – 0.84″ | |
| Vesta | 0.20″ – 0.64″ | |
| Pluto | 0.06″ – 0.11″ | |
| R Doradus | 0.052″ – 0.062″ | |
| Betelgeuse | 0.049″ – 0.060″ | |
| Eris | 0.034″ – 0.089″ | |
| Alphard | 0.00909″ | |
| Alpha Centauri A | 0.007″ | |
| Canopus | 0.006″ | |
| Sirius | 0.005936″ | |
| Altair | 0.003″ | |
| Deneb | 0.002″ | |
| Proxima Centauri | 0.001″ | |
| Alnitak | 0.0005″ | |
| Event horizon of black hole M87* at center of the M87 galaxy, imaged by the Event Horizon Telescope in 2019. | 0.000025″
(2.5×10-5) |
|
| Una estrella como Alnitak a una distancia donde el Telescopio Espacial Hubble acaba de ser capaz de ver | 6×10-10 segundos de arco |


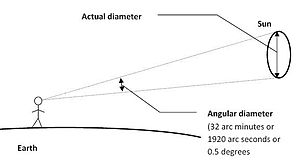
La tabla muestra que el diámetro angular del Sol, visto desde la Tierra, es de aproximadamente 32′ (1920 » o 0,53°), como se ilustra arriba.
Por lo tanto, el diámetro angular del Sol es aproximadamente 250.000 veces mayor que el de Sirio. (Sirio tiene el doble de diámetro y su distancia es de 500.000 veces más; el Sol es 1010 veces más brillante, lo que corresponde a una relación de diámetro angular de 105, por lo que Sirio es aproximadamente 6 veces más brillante por unidad de ángulo sólido.)
El diámetro angular del Sol es también aproximadamente 250.000 veces el de Alpha Centauri A (tiene aproximadamente el mismo diámetro y la distancia es de 250.000 veces más; el Sol es 4×1010 veces más brillante, lo que corresponde a una relación de diámetro angular de 200.000, por lo que Alpha Centauri A es un poco más brillante por unidad de ángulo sólido).
El diámetro angular del Sol es aproximadamente el mismo que el de la Luna. (El diámetro del Sol es 400 veces más grande y su distancia también; el Sol es de 200.000 a 500.000 veces más brillante que la Luna llena (las cifras varían), lo que corresponde a una relación de diámetro angular de 450 a 700, por lo que un cuerpo celeste con un diámetro de 2,5–4″ y el mismo brillo por unidad de ángulo sólido tendría el mismo brillo que la Luna llena.)
Aunque Plutón es físicamente más grande que Ceres, cuando se ve desde la Tierra (por ejemplo, a través del Telescopio Espacial Hubble) Ceres tiene un tamaño aparente mucho mayor.
Los tamaños angulares medidos en grados son útiles para zonas de cielo más grandes. (Por ejemplo, las tres estrellas de la banda cubren aproximadamente 4,5° de tamaño angular. Sin embargo, se necesitan unidades mucho más finas para medir los tamaños angulares de galaxias, nebulosas u otros objetos del cielo nocturno.
Los grados, por lo tanto, se subdividen de la siguiente manera:
- 360 grados (°) en un círculo completo
- 60 minutos de arco (‘) en un grado
- 60 segundos de arco («) en un minuto de arco
Para poner esto en perspectiva, la Luna llena vista desde la Tierra es de aproximadamente 1⁄2°, o 30′ (o 1800″). El movimiento de la Luna a través del cielo se puede medir en tamaño angular: aproximadamente 15° cada hora, o 15″ por segundo. Una línea de una milla de largo pintada en la cara de la Luna aparecería de la Tierra como de 1″ de largo.
En astronomía, es típicamente difícil medir directamente la distancia a un objeto, sin embargo, el objeto puede tener un tamaño físico conocido (quizás es similar a un objeto más cercano con distancia conocida) y un diámetro angular medible. En ese caso, la fórmula de diámetro angular se puede invertir para obtener la distancia de diámetro angular a objetos distantes como
d d 2 D tan ( δ 2 ) {\displaystyle d\equiv 2D\tan \left({\frac {\delta }{2}}\right)}

.
En el espacio no euclidiano, como nuestro universo en expansión, la distancia de diámetro angular es solo una de varias definiciones de distancia, de modo que puede haber diferentes «distancias» al mismo objeto. Ver Medidas de distancia (cosmología).
Objetos no circulareseditar
Muchos objetos de cielo profundo, como galaxias y nebulosas, parecen no circulares y, por lo tanto, suelen tener dos medidas de diámetro: eje mayor y eje menor. Por ejemplo, la Pequeña Nube de Magallanes tiene un diámetro aparente visual de 5° 20′ × 3° 5′.
Defecto de iluminacióneditar
El defecto de iluminación es el ancho angular máximo de la parte no iluminada de un cuerpo celeste visto por un observador dado. Por ejemplo, si un objeto tiene 40″ de arco y está iluminado al 75%, el defecto de iluminación es de 10″.