Distribuciones Normales (Curva de campana): Definición, Problemas verbales

Probabilidad y estadística > Distribuciones normales

Contenido:

1. ¿Qué es una distribución normal?
2. El Modelo Normal Estándar
3. Problemas Verbales de Distribución Normal.
4. Distribución normal en el TI 89 Ejemplos
5. Artículos relacionados.

¿Qué es una distribución Normal?

Una distribución normal.

Una distribución normal, a veces llamada curva de campana, es una distribución que ocurre naturalmente en muchas situaciones. Por ejemplo, la curva de campana se ve en pruebas como el SAT y el GRE. La mayor parte de los estudiantes obtendrán el promedio (C), mientras que un número menor de estudiantes obtendrán una B o D. Un porcentaje aún menor de estudiantes obtendrán una F o una A. Esto crea una distribución que se asemeja a una campana (de ahí el apodo). La curva de campana es simétrica. La mitad de los datos caerá a la izquierda de la media; la mitad caerá a la derecha.Muchos grupos siguen este tipo de patrón. Es por eso que se usa ampliamente en negocios, estadísticas y en organismos gubernamentales como la FDA:

• Heights of people.
• Errores de medición.
• presión Arterial.
• Puntos en una prueba.
• Puntuaciones de CI.
• Salarios.

La regla empírica dice qué porcentaje de sus datos cae dentro de un cierto número de desviaciones estándar de la media:
• el 68% de los datos cae dentro de una desviación estándar de la media.
* el 95% de los datos se encuentran dentro de dos desviaciones estándar de la media.r• * el 99,7% de los datos se encuentran dentro de tres desviaciones estándar de la media.

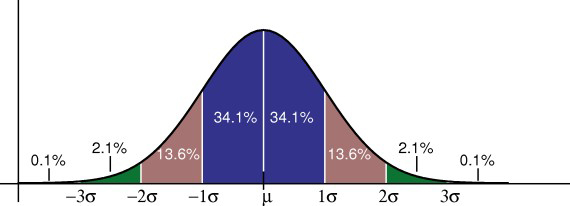
La desviación estándar controla la propagación de la distribución. Una desviación estándar más pequeña indica que los datos están agrupados estrechamente alrededor de la media; la distribución normal será más alta. Una desviación estándar mayor indica que los datos se extienden alrededor de la media; la distribución normal será más plana y más amplia.

Propiedades de una distribución normal

• La media, el modo y la mediana son todos iguales.
• La curva es simétrica en el centro (es decir, alrededor de la media, μ).
• Exactamente la mitad de los valores están a la izquierda del centro y exactamente la mitad de los valores están a la derecha.
• el área total bajo La curva es 1.

El Modelo Normal Estándar
Un modelo normal estándar es una distribución normal con una media de 0 y una desviación estándar de 1.

Modelo normal estándar: Distribución de datos

Una forma de averiguar cómo se distribuyen los datos es trazarlos en un gráfico. Si los datos están distribuidos de manera uniforme, es posible que aparezca una curva de campana. Una curva de campana tiene un pequeño porcentaje de los puntos en ambas colas y el mayor porcentaje en la parte interna de la curva. En el modelo normal estándar, aproximadamente el 5 por ciento de sus datos caerían en las «colas» (de color naranja más oscuro en la imagen de abajo) y el 90 por ciento estaría en el medio. Por ejemplo, para los puntajes de los exámenes de los estudiantes, la distribución normal mostraría que el 2.5 por ciento de los estudiantes obtienen puntajes muy bajos y 2.5 por ciento obteniendo puntuaciones muy altas. El resto estará en el medio; no demasiado alto ni demasiado bajo. La forma de la distribución normal estándar se ve así:

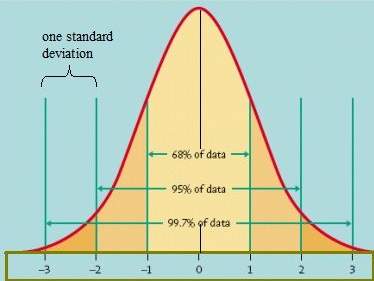
Modelo normal estándar. Crédito de la imagen: Universidad de Virginia.

Aplicaciones prácticas del Modelo Normal Estándar

La distribución normal estándar podría ayudarlo a averiguar en qué asignatura está obteniendo buenas calificaciones y en qué asignaturas debe esforzarse más debido a los bajos porcentajes de puntuación. Una vez que obtenga una puntuación en una asignatura que sea más alta que su puntuación en otra asignatura, podría pensar que es mejor en la asignatura en la que obtuvo la puntuación más alta. Esto no siempre es cierto.

Solo puede decir que es mejor en un tema en particular si obtiene una puntuación con un cierto número de desviaciones estándar por encima de la media. La desviación estándar le indica qué tan apretados están los datos agrupados alrededor de la media; le permite comparar diferentes distribuciones que tienen diferentes tipos de datos, incluidas diferentes medias.

Por ejemplo, si obtiene una puntuación de 90 en Matemáticas y 95 en inglés, podría pensar que es mejor en inglés que en Matemáticas. Sin embargo, en matemáticas, su puntuación es de 2 desviaciones estándar por encima de la media. En inglés, es solo una desviación estándar por encima de la media. Te dice que en Matemáticas, tu puntaje es mucho más alto que la mayoría de los estudiantes (tu puntaje cae en la cola).Basado en estos datos, ¡en realidad te desempeñaste mejor en Matemáticas que en inglés!

Preguntas de probabilidad usando el Modelo estándar

Las preguntas sobre la probabilidad de distribución normal estándar pueden parecer alarmantes, pero la clave para resolverlas es comprender lo que representa el área bajo una curva normal estándar. El área total bajo una curva de distribución normal estándar es del 100% (es decir, «1» como decimal). Por ejemplo, la mitad izquierda de la curva es del 50%, o .5. Así que la probabilidad de una variable aleatoria que aparece en la mitad izquierda de la curva es .5.

Por supuesto, no todos los problemas son tan simples, por lo que hay una tabla z. Todo lo que hace una tabla z es medir esas probabilidades (es decir, 50%) y ponerlas en desviaciones estándar de la media. La media está en el centro de la distribución normal estándar, y una probabilidad de 50% equivale a cero desviaciones estándar.

Distribución normal estándar: Cómo Encontrar la probabilidad (Pasos)

Paso 1: Dibuja una curva de campana y sombra en el área que se solicita en la pregunta. El siguiente ejemplo muestra z >-0.8. Eso significa que está buscando la probabilidad de que z sea mayor que -0.8, por lo que necesita dibujar una línea vertical en -0.8 desviaciones estándar de la media y sombrear todo lo que es mayor que ese número.

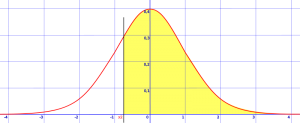
el área sombreada es z > -0.8

Paso 2: Visite el índice de área de probabilidad normal y encuentre una imagen que se parezca a su gráfico. Siga las instrucciones de esa página para encontrar el valor z del gráfico. El valor z es la probabilidad.

Consejo: El paso 1 es técnicamente opcional, pero siempre es una buena idea dibujar un gráfico cuando intentas responder problemas verbales de probabilidad. Esto se debe a que la mayoría de los errores ocurren no porque no puedas hacer las matemáticas o leer una tabla z, sino porque restas una puntuación z en lugar de sumar (es decir, imaginas la probabilidad bajo la curva en la dirección equivocada. Un boceto le ayuda a cimentar en su cabeza exactamente lo que está buscando.

Si todavía tienes problemas, echa un vistazo a los tutores en Chegg.com. ¡Tus primeros 30 minutos con un tutor en vivo son gratis!

Problemas verbales de distribución normal

Este vídeo muestra un ejemplo de un problema verbal de distribución normal. Para obtener más ejemplos, siga leyendo a continuación:

Cuando aborda la distribución normal en una clase de estadísticas, está tratando de encontrar el área debajo de la curva. El área total es del 100% (como decimal, es 1). Los problemas de distribución normales vienen en seis tipos básicos. ¿Cómo sabes que un problema de palabras implica una distribución normal? Busque la frase clave » asumir que la variable está distribuida normalmente «o» asumir que la variable es aproximadamente normal.»Para resolver un problema de palabras, debes averiguar qué tipo tienes.

1. «Entre»: Contiene la frase «entre» e incluye un límite superior y un límite inferior (es decir, «encontrar el número de casas con un precio entre 5 50K y 200K»).
2. «Más que» o «Arriba»: contiene la frase «más que»o » arriba».
3. «Menos Que».
4. Ejemplo de Corte inferior (video)
5. Ejemplo de Corte superior (video)
6. Ejemplo de Porcentaje medio (video)

«Entre»

Este manual cubre la resolución de problemas que contienen la frase «entre» e incluye un límite superior e inferior (es decir, «encontrar el número de casas con un precio entre $50K y 200K»). Tenga en cuenta que esto es diferente de encontrar el «porcentaje medio» de algo.

Problemas verbales con distribución normal:» Entre»: Pasos

Paso 1: Identificar las partes del problema verbal. La palabra problema identificará:

1. La media (promedio o μ).
2. desviación Estándar (σ).
3. Número seleccionado (es decir, «elija uno al azar» o «seleccione diez al azar»).
4. X: los números asociados con «entre» (es decir, «entre 5 5,000 y 1 10,000» tendrían X como 5,000 y como $10,000).

además, se le dará BIEN:

1. Tamaño de la muestra (es decir, 400 casas, 33 personas, 99 fábricas, 378 plomeros, etc.). O
2. Es posible que se le pida una probabilidad (en cuyo caso, el tamaño de la muestra probablemente sea para todos, es decir, «fontaneros oficiales» o «pilotos de primer año».»

Paso 2: Dibuja un gráfico. Ponga la media que identificó en el Paso 1 en el centro. Ponga el número asociado con «entre» en el gráfico (adivine dónde caerían los números, no tiene que ser exacto). Por ejemplo, si su media era de $100, y se le preguntó por «salarios por hora entre 7 75 y 1 125») su gráfico se verá algo como esto:

Paso 3: Calcule las puntuaciones z. Introduce el primer valor X (en mi gráfico de arriba, es 75) en la fórmula del valor z y resuelve. El μ (la media), es 100 del gráfico de muestra. Puede obtener estas cifras (incluida σ, la desviación estándar) de sus respuestas en el paso 1 :

* Nota: si la fórmula lo confunde, todo lo que esta fórmula le pide que haga es:
1. reste la media de X
2. divida por la desviación estándar.

Paso 4: Repita el paso 3 para la segunda X.

Paso 5: Tome los números de los pasos 3 y 4 y utilícelos para encontrar el área en la tabla z.

Si se le pidió que encontrara una probabilidad en su pregunta, vaya al paso 6a. Si se le pidió que encontrara un número de un tamaño de muestra específico, vaya al paso 6b.

Paso 6a:

Convierte la respuesta del paso 5 en un porcentaje.

Por ejemplo, 0.1293 es 12.93%.

Eso es todo–sáltese el paso 6b!

Paso 6b

Multiplique el tamaño de la muestra (que se encuentra en el paso 1) por el valor z que encontró en el paso 4. Por ejemplo, 0,300 * 100 = 30.

Eso es todo!

«Más que»o «Arriba»

Este manual cubre la resolución de problemas de distribución normales que contienen la frase «más que»(o una frase como «arriba»).

Paso 1: Divida el problema de palabras en partes. Encontrar:

1. La media (promedio o μ)
2. Desviación estándar (σ)
3. Un número (por ejemplo, «elija cincuenta al azar» o «seleccione 90 al azar»)
4. X: el número asociado con la instrucción «menos que». Por ejemplo, si se le pidió que encontrara «menos de $9,999», entonces X es 9,999.

Paso 2: Encuentre la muestra del problema. Tendrás un tamaño específico (como «1000 televisores») o una muestra general («Todos los televisores»).

Dibuje un dibujo si el problema con la media y el área que está buscando. Por ejemplo, si la media es de $15 y se le pidió que encontrara qué cenas cuestan más de 1 10, su gráfico podría tener este aspecto:

Paso 3: Calcule la puntuación z (incluya sus valores en el fórmula de valor z y resolver). Usa tus respuestas del paso 1 :

Básicamente, todo lo que está haciendo con la fórmula es restar la media de X y luego dividir esa respuesta por la desviación estándar.

Paso 4: Encuentre el área usando la puntuación z del paso 3. Usa la tabla z. ¿No está seguro de cómo leer una tabla z? Vea el video en la página de la tabla z.

Paso 6: Vaya al Paso 6a para encontrar una probabilidad O vaya al paso 6b para calcular un cierto número o cantidad.

Paso 6a
Convierte la respuesta del paso 5 en un porcentaje.

Por ejemplo, 0.1293 es 12.93%.

Omita el paso 6b: ¡ya está!

Paso 6b
Multiplique el tamaño de la muestra del paso 1 por la puntuación z del paso 4. Por ejemplo, 0,500 * 100 = 50.

¡Ya está!

Menos Que

Este manual cubre la resolución de problemas verbales de distribución normales que tienen la frase «menos que» (o una frase similar como «menos que»).

distribución Normal problemas de palabras menos: Pasos

Paso 1: dividir el problema en partes:

1. La media (o promedio µ)
2. desviación Estándar (σ)
3. Número seleccionado (es decir, «elija uno al azar «o»seleccione diez al azar»)
4. X: el número que va con » menos de «(es decir,» menos de 9 99,000 » enumeraría X como 99,000)

Además, tendrá:

1. Un tamaño de muestra específico. Por ejemplo, 500 botes, 250 sándwiches, 100 televisores, etc.
2. Todos en la muestra (se le pedirá que encuentre una probabilidad). Por ejemplo, «estudiantes de primer año de medicina», «pacientes con cáncer» o » pilotos de aerolíneas.»

Paso 2: Dibuja un dibujo para ayudarte a visualizar el problema. El siguiente gráfico muestra una media de 15 y un área «por debajo de 4»):

Paso 3: Encuentre el valor z conectando los valores dados a la fórmula. La » X » en nuestro gráfico de muestra es 4, y el μ (o media) es 15. Puede obtener estas cifras (incluida σ, la desviación estándar) de sus respuestas en el paso 1, donde identificó las partes del problema:

Todo lo que tiene que hacer para resolver la fórmula es:

1. Restar la media de X.
2. Dividir por la desviación estándar.

Paso 4: Toma el número del paso 3, luego usa la tabla z para encontrar el área.

Paso 5:Para encontrar una probabilidad, vaya al paso 6a. Para encontrar un número de un tamaño de muestra específico, vaya al paso 6b.

Paso 6a

Cambie el número del paso 5 a porcentaje.

Por ejemplo, 0.1293 es 12.93%.

Eso es todo!

Paso 6b

Multiplique el tamaño de la muestra (que se encuentra en el paso 1) por el valor z que encontró en el paso 4. Por ejemplo, 0,300 * 100 = 30.

Eso es todo!

Corte inferior

A veces, en un problema de distribución de palabras normal, se le pedirá que encuentre un» límite inferior de un porcentaje superior «de algo (es decir,»encontrar el punto de corte para aprobar un determinado examen en el que el 40% superior de los participantes del examen aprueba»). Un punto de corte inferior es el punto donde las puntuaciones caerán por debajo de ese punto. Por ejemplo, es posible que desee encontrar dónde está el punto de corte para el 10% inferior de los participantes del examen.

Echa un vistazo a nuestro canal de YouTube para más problemas trabajados.

Distribución normal TI 89 Ejemplos

En estadísticas elementales, a menudo se enfrentará a una pregunta que le preguntará los puntos de corte para un cierto porcentaje de la distribución normal, como el 90% superior o el 10% superior. Si bien resolver este tipo de problemas a mano es engorroso, la calculadora gráfica TI-89 hace un trabajo liviano de encontrar puntos de corte para un porcentaje superior con la función Normal Inversa. Lo que realmente estás haciendo es buscar los puntos de corte para un cierto percentil: por ejemplo, si tiene una lista de calificaciones y desea saber qué puntuación está en el percentil 99, puede usar la función normal inversa para encontrar ese punto de corte porcentual.

Encontrar Puntos de Corte Para un Porcentaje Superior

Problema de la muestra: Los estudiantes de cierta universidad miden en promedio 5 pies y 8 pulgadas (68 pulgadas) de alto. Las alturas se distribuyen normalmente, con una desviación estándar de 2,5 pulgadas. ¿Cuál es el valor que separa el 1% superior de las alturas del resto de la población?

Paso 1: Presione APLICACIONES y use las teclas de desplazamiento para resaltar el Editor de estadísticas/Listas.

Paso 2: Pulse F5 2 1 (esto le llevará a la pantalla Normal Inversa).

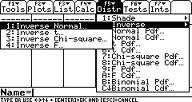
Paso 3: Ingrese 0.99 en el cuadro de Área.

Paso 4: Ingrese 68 en el cuadro μ.

Paso 5: Ingrese 2.5 en el cuadro σ.

Paso 6: Presione ENTRAR.

Paso 7: Lea los resultados: Inverso = 73.8159 significa que la altura de corte para el percentil 99 es de 73.8159 pulgadas.

Eso es todo!

Ejemplo de proporción de probabilidad (función NormalCDF)

Pregunta de muestra: Un grupo de estudiantes con salarios normalmente distribuidos gana un promedio de 6 6,800 con una desviación estándar de 2 2,500. ¿Qué proporción de estudiantes gana entre 6 6,500 y 7 7,300?

Paso 1: Pulse APLICACIONES. Desplácese hasta el Editor de estadísticas/Listas y presione ENTRAR.

Paso 2: Pulse F5 4.

Paso 3: Ingrese 6500 en el cuadro de valor inferior.

Paso 4: Ingrese 7300 en el cuadro de valor superior.

Paso 5: Introduzca 6800 en el μ cuadro.

Paso 6: Ingrese 2500 en el cuadro σ. Pulse INTRO.

Paso 7: Lea la respuesta. Cdf=.127018. En otras palabras,.013, o el 13% de los estudiantes ganan entre 6 6,500 y 7 7,300.

TI-89 Graficando una Curva de distribución normal

El TI-89 no solo puede calcular puntuaciones z y valores de retorno para distribuciones normales, también puede graficar la curva de distribución normal. La representación gráfica de una distribución normal puede ayudarlo a ver qué se supone que debe estar buscando, y le brinda una herramienta más para resolver problemas de distribución normales. El TI-89 puede graficar una curva de distribución normal con un área sombreada para cualquier valor. Por ejemplo, podría crear un gráfico que sea: menos de un cierto número, mayor que un cierto número, o entre un determinado conjunto de números.

Problema de muestra: Dibuje una curva de distribución normal para los salarios de los estudiantes durante un semestre típico. Los salarios de los estudiantes tienen un promedio de 6 6,800 y una desviación estándar de 2 2,500. Sombrear el área en el gráfico que corresponde a salarios entre 7 7,300 y 9 9,000.

Paso 1: Pulse APLICACIONES y seleccione el Editor de Estadísticas / Listas.

Paso 2: Presione F2 3 y F2 4.

Paso 3: Pulse F5) 1.

Paso 4: Desplácese hacia abajo e ingrese 7300 en el cuadro de valor inferior.

Paso 5: Desplácese hacia abajo e ingrese 9000 en el cuadro de valor superior.

Paso 6: Desplácese hacia abajo e ingrese 6800 en el cuadro μ.

Paso 7: Desplácese hacia abajo e ingrese 2500 en el cuadro σ.

Paso 8: Desplácese hacia abajo. Gire la escala automática a » sí » presionando la tecla de desplazamiento derecho, luego la tecla de desplazamiento hacia abajo para seleccionar sí. Pulse INTRO.

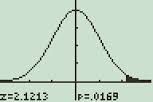
Un gráfico de distribución normal que se muestra en la calculadora TI-89.

Eso es todo!

Tip: Si desea introducir ∞ (infinito) como uno de sus valores inferiores o superiores, pulse la tecla diamante y, a continuación, Catalogue.

Beyer, W. H. CRC Standard Mathematical Tables, 28ª ed. Boca Raton, FL: CRC Press, págs. 533 y 534, 1987.
Feller, W. An Introduction to Probability Theory and Its Applications, Vol. 1, 3rd ed. Nueva York: Wiley, 1968.Kenney, J. F. and Keeping, E. S. Mathematics of Statistics, Pt. 2, 2nd ed. Princeton, NJ: Van Nostrand, 1951.Kraitchik, M. » The Error Curve.»§6.4 en Recreaciones matemáticas. Nueva York: W. W. Norton, pp 121-123, 1942.Patel, J. K. and Read, C. B. Manual de la Distribución Normal. Nueva York: Dekker, 1982.

1. ¿Cuál es la Regla 68-95-99.7?
2. Transformación de Caja Cox
3. Transformación de caja Muller
4. Modelos de mezcla Gaussiana.
5. ¿Qué es un Gráfico de Probabilidad Normal?
6. Cómo calcular una puntuación Z en Estadísticas
7. Encuentre el área a la derecha de una puntuación z.
8. Usando la Aproximación Normal para resolver un Problema Binomial
9. ¿Cuál es el factor de corrección de continuidad?
10. Área Bajo un Índice de Curva de Distribución Normal
11. Teorema del Límite Central.
12. La Distribución Normal Sesgada.
13. Curva Normal de Dos Colas.
14. La Función Q.

——————————————————————————

Necesito ayuda con una tarea o cuestión de prueba? Con Chegg Study, puede obtener soluciones paso a paso a sus preguntas de un experto en el campo. ¡Tus primeros 30 minutos con un tutor de Chegg son gratis!