Máxima Parsimonia en redes Filogenéticas

Definición de redes filogenéticas

Seguimos la definición de redes filogenéticas que se da en, Definición 4, página 16]. Para todas las demás definiciones gráficas teóricas que no se dan aquí, seguimos . Una red filogenética enraizada, llamada simplemente aquí red filogenética, se define como un gráfico acíclico enraizado, dirigido (DAG), cuya raíz tiene grado 0 y las hojas tienen grado 0. Los vértices cuyo grado de inclinación es mayor que 1 se denominan vértices reticulados y las aristas con vértices reticulados como vértices de cabeza se denominan aristas reticuladas. Todos los demás bordes se denominan bordes de árbol. La definición dada en se ocupa de la llamada restricción de» consistencia temporal», es decir, que los bordes de los árboles tienen lugar en un tiempo positivo y los vértices reticulados tienen padres que solo pueden»coexistir en el tiempo». Por lo tanto, en adelante, recordamos la definición formal de redes filogenéticas como se da en .

Dado cualquier grafo dirigido, decimos que dos vértices u y v no pueden coexistir en el tiempo si existe una secuencia P = (p1, p2,…, p, k ) de las rutas en N tal que:

1. p i es una trayectoria que contiene al menos un árbol de la orilla, para cada 1 ≤ i ≤ k,

2. u es la cola de p 1, y v es la cabeza de p, k , y

3. para cada 1 ≤ i ≤ k – 1, existe una red de vértices cuyos dos padres están a la cabeza de p i y la cola de p i+1.

Una red filogenética N es un DAG arraigado que obedece a las siguientes restricciones:

1. Cada vértice tiene indegree y outdegree definido por una de las cuatro combinaciones (0, 2), (1, 0), (1, 2), or (2, 1) – correspondiente a, respectivamente, la raíz, las hojas, los vértices internos de los árboles y los vértices reticulados. Todos los vértices que no sean vértices reticulados se denominan vértices de árbol.

2. Si dos vértices u y v no pueden coexistir en el tiempo, entonces no existe una red vértice w con aristas (u, w) y (v, w).

3. Dado cualquier borde de la red, al menos uno de sus extremos debe ser un vértice de árbol.

Otro componente de esta definición es que para cualquier borde de la red filogenética, al menos uno de sus extremos (ya sea la cabeza o la cola) es un vértice de árbol. Aquí, usaremos esta definición. En la medida de lo posible, señalamos si las condiciones de la definición son necesarias.

Las redes filogenéticas pueden considerarse ingenuamente como una red que contiene como subgrafos, los árboles que explican las historias evolutivas de diferentes segmentos de las secuencias terminales de entrada. Dada una red filogenética, eliminar uno de cada borde incidente en un vértice reticulado no garantiza un árbol filogenético resultante con el mismo conjunto de hojas que el de la red. Esta es una propiedad indeseable, especialmente si el criterio de parsimonia se define encontrando un árbol filogenético dentro de la red que es más parsimonioso para el sitio dado, como se define en . Para evitar este problema, es necesario asumir que ningún vértice interno tiene dos hijos reticulados. Llamamos a esta clase de redes filogenéticas una red filogenética sin reticulaciones hermanas. Vea la Figura 1 para algunos ejemplos de redes filogenéticas.

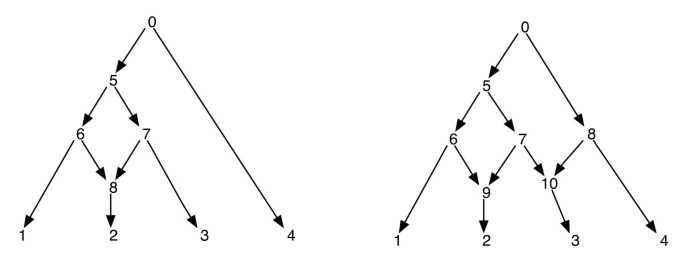
Filogenético de las Redes. La figura muestra dos redes filogenéticas; la de la izquierda tiene solo un vértice reticulado y la de la derecha tiene dos vértices reticulados que son hermanas entre sí. Tenga en cuenta que la eliminación de los bordes (7, 9) y (7, 10) de la red de la derecha no da lugar a un árbol en el que el vértice 7 sea una hoja. Esto muestra que la eliminación de un borde entrante por vértice reticulado no produce necesariamente un árbol con el mismo conjunto de hojas que la red. El post de pedidos y la pre-orden de los vértices de la red de la izquierda son 1, 2, 8, 6, 3, 7, 5, 4, 0 y 0, 5, 6, 1, 8, 2, 7, 3, 4 respectivamente, y para la red de la derecha, ellos son 1, 2, 9, 6, 3, 10, 7, 5, 4, 8, 0 y 0, 5, 6, 1, 9, 2, 7, 10, 3, 8, 4 respectivamente.

Antes de proceder a la definición de los problemas de parsimonia, la siguiente es una observación útil. Para una red filogenética N sin reticulaciones hermanas, y con vértices reticulados r y con conjunto de hojas X, denotamos T ( N ) como el conjunto de todos los árboles contenidos en N. Cada árbol se obtiene siguiendo dos pasos: (1) para cada vértice reticulado, eliminar uno de los bordes entrantes, y luego (2) para cada vértice v de grado indegree y outdegree 1, cuyo padre es u y el hijo es w, contraer los bordes (u, v) y (v, w) en un solo borde (u, w). La condición de que cada borde en N tenga un vértice de árbol como punto final y que cada vértice de árbol tenga al menos un vértice de árbol como hijo, asegura que el conjunto de hojas del árbol resultante sea el mismo que el de la red. Por lo tanto, el conjunto T ( N ) contiene exactamente 2 árboles filogenéticos cuyo conjunto de hojas es exactamente X.

Parsimonia máxima

Nos referimos a los lectores para una descripción general de la idea de parsimonia y para la discusión de varios algoritmos de parsimonia. Se ha señalado que el método de parsimonia para árboles puede extenderse a redes filogenéticas. En una serie de artículos , uno de estos criterios de parsimonia se define al encontrar un árbol en la red que tenga la mejor puntuación parsimoniosa, y se han ideado algoritmos eficientes para optimizar este criterio en una red filogenética dada. Aunque se ha demostrado que estos algoritmos funcionan bien en la práctica, solo pueden funcionar correctamente para redes filogenéticas sin reticulaciones hermanas, ya que es sencillo buscar un árbol óptimo en esta clase restringida de redes. En esta sección, indicamos una versión alternativa del problema de parsimonia y en las secciones siguientes proporcionamos algunas soluciones heurísticas para optimizar la puntuación en cualquier red filogenética.

Let = {1, 2, …, n} denota el conjunto de etiquetas de hojas de una red filogenética dada función N. A λ: → {0, 1, …,| Σ / – 1} se denomina función de asignación de estados sobre el alfabeto Σ (un conjunto no vacío) para N. Decimos que una función λ ^: V (N ) → { 0 , 1 , … , | Σ / – 1 } es una extensión de λ sobre N si está de acuerdo con λ en las hojas de N. Para un vértice v en N, llamamos a λ ^ (v) como una asignación de λ ^ en v. Una red totalmente asignada es una red en la que todos los vértices tienen etiquetas de {0, 1, …, |Σ| – 1}. Sea C una matriz de costes cuya entrada ij c ij es el coste de transformación del estado i al estado j a lo largo de cualquier arista en N. Si e = (u, v) es una arista en N, donde u es el padre de v, denotamos w e ( λ ) ^ = c i j , donde i= λ ^ ( u ) y j= λ ^ ( v ) . Para un gráfico G, dejamos que E (G) denote el conjunto de aristas de G. Entonces el problema de parsimonia se define de la siguiente manera.

Entrada: Un filogenético de la red N con la hoja de etiquetas y un estado de la función de asignación de λ sobre el alfabeto Σ para N.

Parsimonia criterio: Para una extensión λ ^ λ, vamos

y

Salida: Dado P ∈ {P1, P2}, encuentre λ ^ que minimice P (λ^).

Notamos que P 1 (λ^) se introduce en y P 2 ( λ^) es la definición que usaremos en este artículo. Un enfoque más general es minimizar Q ( λ ^ ) = ∑ e ∈ E ( N ) d e ( w e ( λ ^ ) ) , donde d e es una función de peso no negativa en los bordes de N. Para los propósitos de este artículo, nos restringimos a P = P2, aunque el primero de nuestros enfoques, la solución de programación dinámica también se aplica a P = Q.

Algoritmos de Parsimonia en redes

Que Atraviesan una red filogenética

En una red, el recorrido de vértices se refiere al proceso de visitar cada vértice, exactamente una vez, de manera sistemática. Tales traversales se clasifican por el orden en que se visitan los vértices. Necesitamos dos tipos de traversales de vértices de red para describir nuestros algoritmos. Estos son bien conocidos por los árboles filogenéticos, y los presentamos aquí para las redes filogenéticas. Los algoritmos para los traversales dados a continuación comienzan desde cualquier vértice v dado en la red. En este trabajo, siempre realizaremos los traversales desde el vértice raíz de la red.

Recorrido por pedido anticipado de una red filogenética desde un vértice v

1. Visite el vértice v.

2. Realice recursivamente el recorrido por pedido anticipado de cada niño que aún no ha sido visitado.

Recorrido post-orden de una red filogenética desde un vértice v

1. Realice recursivamente el recorrido post-orden de cada niño que aún no ha sido visitado.

2. Visita el vértice v.

Dado que una red filogenética es un DAG, tales traversales visitarán todos los vértices de la red exactamente una vez. (Consulte para obtener más detalles sobre la existencia de tales traversales en DAG). A los efectos de este artículo, asumimos que los vértices de una red están etiquetados de forma única por enteros. Tenga en cuenta que las hojas ya están etiquetadas del conjunto ; y así usamos otros enteros para otros vértices. Cada vez que se extraen los vértices secundarios de v, también se ordenan en orden creciente de sus etiquetas enteras y las traversales pre y post orden se realizan en este orden. Esto asegurará lo siguiente: si los vértices v y v’ son tales que no hay una ruta dirigida entre ellos, entonces el vértice v se atraviesa antes del vértice v’ en el pre-orden si y solo si el vértice v se atraviesa antes del vértice v’ en el post-orden. Vea la Figura 1 para ver algunos ejemplos. Con esta propiedad, notamos que los traversales pre – y post-orden de la raíz de una red filogenética trazan cada uno el mismo árbol de expansión, que llamamos aquí el árbol de travesía.

Solución de programación dinámica

La programación dinámica se utiliza para proporcionar soluciones eficientes para encontrar la puntuación de parsimonia exacta cuando la red es un árbol filogenético . En esta sección, mostramos que el mismo enfoque se puede generalizar a las redes filogenéticas. El algoritmo de Sankoff en un árbol atraviesa los vértices del árbol a través del post-orden mientras calcula los costos mínimos de cada estado en cada vértice desde las hojas hasta la raíz, y luego elige las mejores asignaciones en cada vértice retrocediendo desde la raíz hasta las hojas atravesando los vértices del árbol a través del pre-orden. Ambas fases se presentan para redes en Algoritmos 1 y 2 respectivamente. Las describimos brevemente a continuación. Se puede notar que si la red es un árbol, entonces nuestros algoritmos coinciden con las fases de pre-pedido y post-pedido del método de Sankoff para árboles.

Dada una red filogenética N, con vértices foliares etiquetados y con función de asignación de estados λ sobre el alfabeto Σ, asigne a cada vértice v ∈ V una cantidad S v (i) para cada i ∈ Σ. En árboles filogenéticos, S v (i) denota la suma mínima de costos de todos los eventos desde el vértice v a todas las hojas a las que se puede llegar desde v, dado que a v se le asigna el estado i y a todos los vértices descendientes de v se les asigna un estado. En las redes, no hay una forma sencilla de calcular tal cantidad. En su lugar, permitimos que S v (i) sea un límite inferior de la puntuación exacta anterior y se calcula durante la fase de recorrido posterior al pedido.

Fase transversal post-orden: Si v es una hoja de N, entonces S v (i) se asigna 0 si el estado observado es el estado i, e infinito de lo contrario. Ahora todo lo que necesitamos es una relación de recursión para calcular S v (i) para el resto de los vértices. Para cada hijo w de v, decimos que w satisface la condición de recorrido posterior al pedido con respecto a v, o simplemente condición de recorrido con respecto a v en vista de la observación al principio de esta sección, si se mantiene lo siguiente:

1. (i)

   El vértice w es un vértice reticulado y

2. (ii)

   si v’ es el padre de w distinto de v, entonces el vértice v debe ser atravesado antes de v’ en el recorrido post-orden de N.

Ahora definimos recursivamente para cada arista (v, w),

Para un árbol filogenético, s(v, w)(i) siempre asume la primera de estas cantidades, y por lo tanto da la suma de los costos de sustitución a lo largo de los bordes del árbol que se encuentran debajo del vértice v, siempre que al vértice v se le asigne el estado i. Para las redes filogenéticas, para tener en cuenta los costos de sustitución a lo largo de los bordes que se encuentran debajo de un vértice reticulado w solo una vez cuando al vértice v se le asigne el estado i, dejamos que el v ‘padre’ de w el árbol transversal tiene en cuenta todos los costos de sustitución a lo largo de todos los bordes que se encuentran por debajo de v. Por otro lado, si v no es un padre de w en el árbol transversal, s(v, w)(i) simplemente denota el costo de sustitución del estado i en el vértice v a otro estado en w que es menos costoso.

a continuación definimos

donde la suma se ejecuta para todos los niño(s) vértice(s) w de v. Como se mencionó anteriormente, en árboles filogenéticos, S v (i) denota la suma mínima posible de costos de sustitución a lo largo de todas las aristas desde el vértice v hasta todas las hojas a las que se puede llegar desde v, dado que a v se le asigna el estado i y a todos los vértices a los que se puede llegar desde v se les asigna un estado.

En redes filogenéticas, al calcular s(v, w) (i) donde w es un vértice reticulado tal que (v, w) no es un borde en el árbol transversal, no hay conocimiento previo del estado que se asignará más tarde en el vértice reticulado w. Por lo tanto, s(v, w)(i) solo puede ser un límite inferior de los bordes de la red que se encuentran debajo del vértice v, si al vértice v se le asigna el estado i. El razonamiento para esto es que s(v, w)(i) es el costo de sustitución del estado i en el vértice v a otro estado en w que es menos costoso, en lugar del costo de sustitución del estado i en v al estado en w que se asignará más tarde. Dado que la definición de S v (i) depende de la definición de s (v, w) (i), y se definen recursivamente, observamos lo siguiente: S v (i) es un límite inferior en la suma de los costos de sustitución a lo largo de los bordes de la red a los que se puede acceder desde el vértice v, siempre que a v se le asigne el estado i y a todos los vértices del árbol descendiente se les asigne un estado único, y a los vértices reticulados se les asignen dos estados que no son necesariamente los mismos. Los estados asignados del vértice reticulado contribuyen a un conflicto si los estados no son los mismos. Supongamos que el estado i se asigna al vértice raíz r, y a todos los vértices de árbol se les asigna un estado único, mientras que a los vértices reticulados se les asignan dos estados. Luego, el costo S r (i) denota la suma mínima posible de costos de sustitución a lo largo de todas las aristas de un árbol transversal con uno de los estados asignados para vértices reticulados, más la suma de los costos de sustitución a lo largo de las aristas reticuladas restantes con el estado de asignación alternativo en los vértices reticulados. Dado que buscamos una asignación en los vértices de la red sin conflictos en los vértices reticulados, S r (i) es un límite inferior en el costo de dicha asignación donde se asigna el vértice raíz i y todos los vértices se asignan con una asignación única.

Durante esta fase, también almacenamos los estados

para poder retroceder el estado de w que alcanza la cantidad s(v, w) (i) durante la fase de pre-pedido. Véase Algoritmo 1.

Pre-orden de la fase transversal: Primero elegimos el mínimo

donde r es el vértice raíz y asignamos el estado que alcanza el mínimo en el vértice raíz, es decir., sea λ ^ (r ) = i r tal que S r (i r) = S. Para cualquier otro vértice w que no sea un vértice reticulado, cuyo padre v ya esté asignado con un estado i, asignamos el estado t(v, w) (i). Para un vértice reticulado w cuyos vértices principales son v y v’, supongamos que a v y v’ se les asignan estados i e i’ respectivamente al atravesar por el pre-orden. Los posibles estados j = t(v, w)(i) y j’ = t(v’, w)(i’) de w que lograr s(v, w)(i) y s(v, w)(i’), respectivamente, no tiene que ser el mismo. En otras palabras, es posible que j ≠ j’. En este caso, tenemos un conflicto en el vértice reticulado w. Por lo tanto, la técnica de programación dinámica no da una extensión para λ cuya puntuación de parsimonia es S. En este caso, simplemente elegimos entre j y j’ para λ(w) de acuerdo con cuál de los vértices entre v y v’ se atraviesa primero en el pre-orden. Por lo tanto, si el vértice w satisface la condición transversal con respecto a v, tenemos λ ^ ( w ) =j.

Después de completar la fase de preorden, podemos obtener la puntuación correspondiente a la extensión λ ^ configurando primero S’ = S y actualizando S ‘ en cada vértice reticulado w de la siguiente manera: La puntuación del límite superior S’ se actualiza correspondiente a la asignación j en el vértice w como S ‘- c i ‘ j ‘+c i ‘ j . Ver Algoritmo 2. La Figura 2 muestra un ejemplo de cómo se ejecuta el algoritmo en una red. Dado que S r (i) es un límite inferior en la asignación óptima donde se asigna el vértice raíz i y todos los vértices se asignan con una asignación única, y dado que S = min i S r (i), concluimos que S es un límite inferior del óptimo que buscamos encontrar. Vea el Lema 1 para una prueba formal.

programación Dinámica solución. La solución de programación dinámica aplicada a una red filogenética. Los estados son 0, 1 y 2. La matriz de costes utilizada tiene todos los 1s excepto los elementos diagonales que son todos 0s. Las tablas mostradas en cada vértice v son los costes, S v (i) (segunda fila) de cada estado, i (primera fila) que se calculan durante el recorrido posterior al pedido. También se muestran en los vértices los estados del vértice secundario w, es decir, la t (v, w) (i) (tercera fila) que corresponden a los costos de la segunda fila; cuando hay dos hijos para un vértice, las entradas de la tercera fila se representan como un par de estados del hijo izquierdo y el hijo derecho, respectivamente. Cada arista(v, w) se etiqueta con s(v, w) (i) para cada estado i. Durante el recorrido de pre-pedido, se seleccionan los estados para cada vértice (se muestra en negrita). El costo de 2 resaltados en negrita en el vértice raíz da un límite inferior, S. El estado asignado en cada vértice se resalta en negrita. El algoritmo encuentra un total de tres sustituciones (resaltadas por aristas en negrita). Esto se debe a que los estados asignados en los vértices primarios del vértice reticulado dan asignaciones conflictivas de 1 y 2 respectivamente, de las cuales el estado 1 se asigna en el vértice reticulado. Por lo tanto, con un costo adicional de 1, obtenemos la puntuación de 3 (un límite superior de la puntuación óptima) como la puntuación de parsimonia correspondiente a la asignación mostrada. Tenga en cuenta que la puntuación de parsimonia óptima en la red es 2 (igual al límite inferior), que se puede encontrar mediante una búsqueda exhaustiva y se puede realizar cambiando la asignación de 1 a 2 para el padre izquierdo del vértice reticulado y de 1 a 2 para el vértice reticulado. Por lo tanto, el límite inferior coincide con la puntuación óptima, aunque la asignación correspondiente al límite inferior no está libre de conflictos y no es la misma que la asignación correspondiente al óptimo.

Lema 1. La cantidad S es un límite inferior de la puntuación de parsimonia óptima en la red N.

Proof. Por la construcción de S, tenemos

donde el segundo sumando es para el vértice reticulado w con padres son v y v’, de tal manera que v satisface el recorrido condición w.r.t. w. Por lo tanto , el costo c λ ^ ( v), λ ^ ( w ) es el costo de sustitución del estado asignado λ ^ ( v ) en v al estado λ ^ ( w ) en w. Por otro lado , el costo c λ ^ ( v’), t ( v’, w ) ( λ ^ ( v ‘) ) es el costo de sustitución del estado asignado λ ^ ( v ) en v al estado t ( v’, w ) ( λ ^ ( v ‘) ) en w. Tenga en cuenta que el estado t ( v’, w ) ( λ ^ ( v ‘ ) ) no es necesariamente el mismo que el estado λ ^ ( w), y S es el mínimo entre todas las asignaciones que pueden resultar en conflictos en los vértices reticulados.

Supongamos que S ^ es la puntuación de parsimonia óptima en N con la función μ: V (N) → {0, 1, …,| Σ / – 1} como extensión de λ tenemos

donde en el segundo sumando w es un vértice reticulado con los padres v y v’. Dado que μ es una asignación libre de conflictos que está contenida en el conjunto de todas las asignaciones entre cuyos costos S es el mínimo (compare la ecuación (3) y (4)), tenemos S≤ S ^ . □

Ahora para la complejidad del algoritmo. Supongamos que la red N tiene n hojas y r vértices reticulados. Entonces el número de vértices en N es 2(n + r) -1. En cada vértice v y para cada estado i, la cantidad S se puede calcular en tiempo O (k2), donde k = |Σ|. El paso transversal de pre-orden implica encontrar S en complejidad O (k) y asignar los mejores estados para cada vértice. Además, arreglar estados de vértices reticulados conflictivos toma tiempo O (r). Por lo tanto, la complejidad del algoritmo (presentado aquí) para encontrar un límite inferior y un límite superior es O((n + r)k2). Se puede obtener un límite superior alternativo en O (nk2) simplemente asignando durante la fase transversal post-orden, para cada vértice reticulado el estado que ocurre el número máximo de veces en las hojas alcanzables desde el vértice reticulado respectivo; y procediendo a través de la búsqueda de S v (i) para los vértices restantes. El óptimo exacto también se puede obtener restringiendo los estados posibles a un solo estado para cada vértice reticulado, ejecutando el algoritmo de programación dinámica para cada una de las combinaciones de estados kr para los vértices reticulados, y eligiendo el mínimo entre todos ellos. La complejidad temporal de este proceso es O (nkr+2).

Algoritmo 1 Fase transversal post-orden: Calcule el costo de cada estado en cada vértice

1. 1:

   Entrada: Red N y los estados observados de Σ en las hojas de N, es decir, una función de asignación de estados λ sobre el alfabeto Σ para N.

2. 2:

   Para cada hoja v, sea S v (i) = 0 si λ(v) = i y ∞ de lo contrario.

3. 3:

   Repetir en orden posterior para cada vértice interno (raíz, vértice de árbol interno o vértice reticulado) v en N: Para cada estado i, calcule S v (i) dado en(1) y t(v, w) (i) para cada hijo w de v, dado en (2).

4. 4:

   Salida: {(S, v (i)): v ∈ V (N), i ∈ Σ}.

Minimizar el número de mutaciones en una red filogenética

El algoritmo de Fitch cuenta el número de cambios en un árbol filogenético bifurcado para cualquier conjunto de caracteres, donde los estados pueden cambiar de cualquier estado a cualquier otro estado. Por lo tanto, la matriz de costos es tal que sus elementos diagonales son todos ceros y los elementos fuera de la diagonal son todos unos. En esta sección, mostramos cómo el algoritmo de Fitch se extiende a encontrar límites superiores e inferiores para el número de cambios evolutivos en una red filogenética dada. Primero, mostramos que el algoritmo de Fitch se puede extender para dar un límite superior para la puntuación de parsimonia óptima. Como antes, las fases transversales de post-orden y pre-orden se dan en los Algoritmos 3 y 4 a continuación. Consulte la Figura 3 para ver un ejemplo de ejecución del algoritmo.

Fitch-tipo de solución. La solución de tipo Fitch aplicada a la misma red filogenética y los datos de hoja de la Figura 2. A cada vértice se le asigna un conjunto de todos los estados posibles, junto con una puntuación cuando los vértices de la red se atraviesan en orden posterior. La puntuación en la raíz da un límite superior para la puntuación óptima. Las asignaciones de estado se dan durante la fase transversal de pre-orden y el número de sustituciones coincide con la puntuación en la raíz.

Fase transversal de pre-pedido del algoritmo 2: Calcule los límites inferior y superior del óptimo y la asignación correspondiente del límite superior

1. 1:

   Entrada: {(S v (i),): v ∈ V (N), i ∈ Σ}.

2. 2:

   Let S = min i S r ( i), donde r es el vértice raíz y let λ ^ (r ) =arg min i S r (i ) .

3. 3:

   Let S’ = S

4. 4:

   Para cada vértice w en pre-orden cuyo vértice padre v precede inmediatamente a w en el pre-orden, let λ ^ ( ω ) = t v , w ( i ) , donde i= λ ^ ( v ) .

5. 5:

   Visite cada vértice reticulado w con los padres v y v ‘de forma que w satisfaga la condición transversal con respecto a v, con i= λ ^ ( v ) , i’ = λ ^ ( v ‘) , j ‘= t ( v ‘, w ) ( i ) y actualice S’ de la siguiente manera:

   S ‘← S ‘- c i ‘ j ‘+ c i ‘ j .

6. 6:

   Salida: (Límite inferior, Límite superior) = (S, S’); extensión correspondiente a la puntuación del límite superior S ‘ : λ ^ .

Algoritmo 3 Fase transversal Post-orden: Calcular el valor óptimo

1. 1:

   Entrada: Red filogenética N y una función de asignación de estados λ sobre el alfabeto Σ para N.

2. 2:

   Para cada hoja v de N, se nos da A(v) = {λ(v)}, un conjunto de un solo elemento que contiene el estado observado en la hoja.

3. 3:

   Set UB = 0.

4. 4:

   Recurse usando post-orden: Para un vértice v de T con hijos w1 y w2, let y Si el vértice v tiene un solo hijo w, entonces

y