ebben a szakaszban megtanuljuk, hogyan kell építeni és használni egy egyszerű lineáris regressziós modell átalakításával prediktor x értékeket. Ez lehet az első dolog, amit megpróbál, ha nemlineáris tendenciát talál az adataiban. Vagyis az x értékek átalakítása akkor megfelelő, ha a nem-linearitás az egyetlen probléma (azaz a függetlenség, a normalitás és az egyenlő variancia feltételek teljesülnek). Ne feledje azonban, hogy szükség lehet A nemlinearitás kijavítására, mielőtt értékelné a normalitást és az egyenlő variancia feltételezéseket. Is, míg egyes feltételezések úgy tűnik, hogy tartsa alkalmazása előtt a transzformáció, lehet, hogy már nem tart, ha a transzformáció alkalmazzák. Más szavakkal, a transzformációk használata egy iteratív folyamat része, ahol az összes lineáris regressziós feltételezést minden iteráció után újra ellenőrzik.
ne feledje, hogy bár itt egy egyszerű lineáris regressziós modellre összpontosítunk, az alapvető elképzelések általánosabban vonatkoznak a több lineáris regressziós modellre is. Figyelembe vehetjük bármelyik prediktor átalakítását azáltal, hogy megvizsgáljuk a maradványok szórólapjait az egyes prediktorokkal szemben.
A modell felépítése
példa. Az adattranszformációk megismerésének legegyszerűbb módja a példa. Vizsgáljuk meg egy memória-megőrzési kísérlet adatait, amelyben 13 alanyot kértek fel a leválasztott elemek listájának memorizálására. Az alanyokat ezután arra kérték, hogy különféle időpontokban, egy héttel később visszahívják az elemeket. Az elemek arányát (y = prop) különböző időpontokban (x = idő, percben) a lista memorizálása óta rögzítették (wordrecall.txt) és ábrázolva. Felismerve, hogy nincs jó ok arra, hogy a hibakifejezések ne lennének függetlenek, értékeljük a modell fennmaradó három feltételét — linearitás, normalitás és egyenlő varianciák—.
a kapott illesztett Vonaldiagram azt sugallja, hogy a visszahívott elemek (y) aránya nem lineárisan kapcsolódik az időhöz (x):
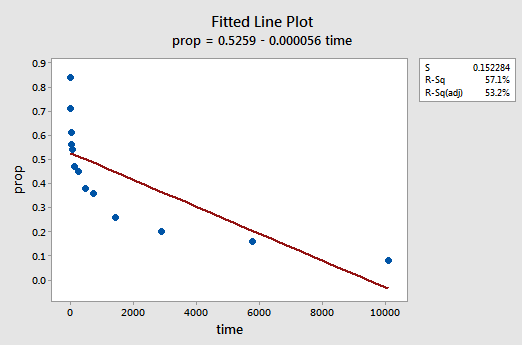
a maradványok vs.illik telek is azt sugallja, hogy a kapcsolat nem lineáris:
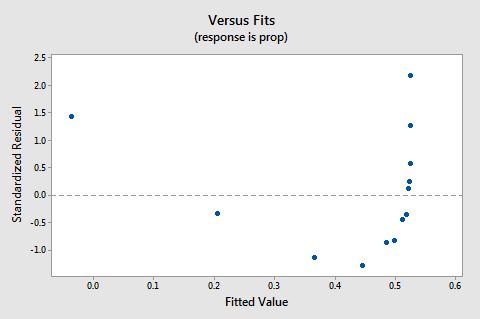
mivel a linearitás hiánya uralja a telket, nem használhatjuk a telket annak értékelésére, hogy a hiba varianciák egyenlőek-e vagy sem. Meg kell oldanunk a nemlinearitás problémáját, mielőtt felmérhetnénk az egyenlő varianciák feltételezését.
mi a helyzet a maradványok normál valószínűségi diagramjával? Mit javasol a hiba feltételeiről? Megállapíthatjuk, hogy ezek általában eloszlanak?
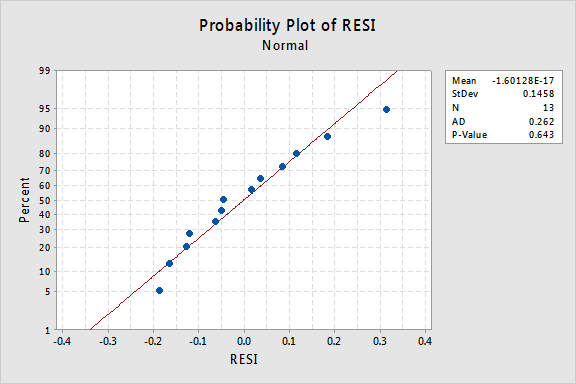
az Anderson-Darling P-érték ebben a példában 0,643, ami arra utal, hogy nem utasítjuk el a normál hibakifejezések nullhipotézisét. Nincs elegendő bizonyíték arra a következtetésre, hogy a hibák feltételei nem normálisak.
összefoglalva, van egy adatkészletünk, amelyben a nemlinearitás az egyetlen fő probléma. Ez a helyzet sikoltozik, mert csak a prediktor értékeit alakítja át. Mielőtt ezt megtesszük, vessünk egy félre, és beszéljük meg a” logaritmikus transzformációt”, mivel ez a leggyakoribb és leghasznosabb adatátalakítás.
a logaritmikus transzformáció. Az alapértelmezett logaritmikus transzformáció csupán magában foglalja a természetes logaritmus — jelölt Ln vagy loge vagy egyszerűen log — az egyes adatértékek. Fontolóra vehetnénk egy másfajta logaritmust, például a 10.naplóbázist vagy a 2. naplóbázist. Azonban a természetes logaritmus — amely úgy tekinthető log bázis e ahol e az állandó 2,718282… — a tudományos munkában használt leggyakoribb logaritmikus skála.
a természetes logaritmikus függvény általános jellemzői:
- az x természetes logaritmusa az e = 2,718282 ereje… hogy meg kell venni annak érdekében, hogy X. Ez lehet jelölni, mint Ln(ex) = x. például, a természetes logaritmusa 5 az a hatalom, amelyre meg kell emelni e = 2,718282… annak érdekében, hogy 5. Mivel a 2,7182821,60944 körülbelül 5, azt mondjuk, hogy az 5 természetes logaritmusa 1,60944. Megjegyzendő, hogy Ln (5) = 1,60944.
- az e természetes logaritmusa egyenlő eggyel, azaz ln(e) = 1.
- az egyik természetes logaritmusa nulla, azaz ln(1) = 0.
a természetes logaritmus függvény diagramja:
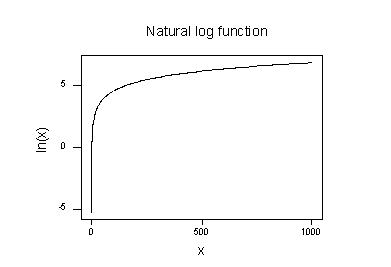
azt sugallja, hogy a természetes logaritmikus transzformáció hatásai a következők:
- az egymáshoz közeli kis értékek tovább terjednek.
- az elosztott nagy értékek közelebb kerülnek egymáshoz.
vissza a példához. Használjuk a természetes logaritmust az X értékek átalakításához a memória megőrzési kísérlet adataiban. Mivel x = az idő a prediktor, csak annyit kell tennünk, hogy az adatkészletben megjelenő minden egyes időérték természetes logaritmusát vesszük. Ennek során létrehozunk egy újonnan átalakított prediktort, az lntime-t:
| time | prop | lntime |
| 1 | 0.84 | 0.00000 |
| 5 | 0.71 | 1.60944 |
| 15 | 0.61 | 2.70805 |
| 30 | 0.56 | 3.40120 |
| 60 | 0.54 | 4.09434 |
| 120 | 0.47 | 4.78749 |
| 240 | 0.45 | 5.48064 |
| 480 | 0.38 | 6.17379 |
| 720 | 0.36 | 6.57925 |
| 1440 | 0.26 | 7.27240 |
| 2880 | 0.20 | 7.96555 |
| 5760 | 0.16 | 8.65869 |
| 10080 | 0.08 | 9.21831 |
We take the natural logarithm for each value of time and place the results in their own column. Vagyis minden prediktor időértéket” átalakítunk ” ln(idő) értékre. Például ln(1) = 0, ln(5) = 1,60944, ln(15) = 2,70805 stb.
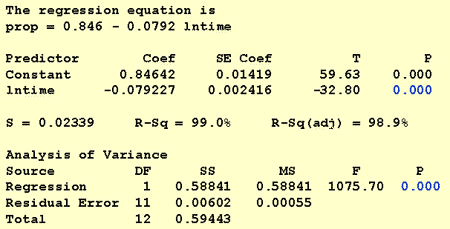
most, hogy átalakítottuk a prediktor értékeket, nézzük meg, segített-e kijavítani az adatok nemlineáris trendjét. Újra illesztjük a modellt y = prop mint válasz és x = lntime mint prediktor.
a kapott illesztett Vonaldiagram azt sugallja, hogy a prediktor értékek természetes logaritmusának felvétele hasznos.
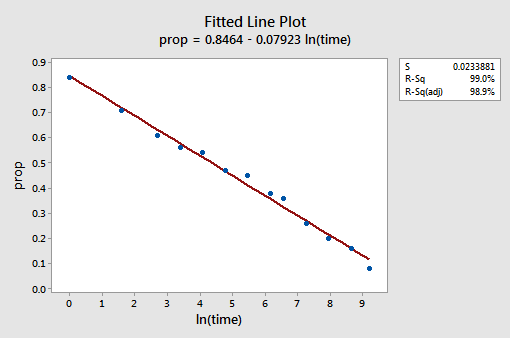
valójában az R2 érték 57,1% – ról 99,0% – ra nőtt. Azt mondja nekünk, hogy a visszahívott szavak (prop) arányának 99% – a csökken, ha figyelembe vesszük az idő természetes naplóját (lntime)!
az új maradék vs. illik diagram jelentős javulást mutat a nem átalakított adatok alapján.
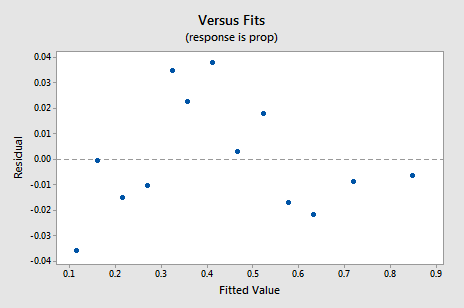
lehet, hogy aggódni valamilyen felfelé-lefelé ciklikus trend a telek. Ismét figyelmeztetem Önt, hogy ne értelmezze túl ezeket a parcellákat, különösen, ha az adatkészlet ilyen kicsi. Valójában nem szabad elvárnia a tökéletességet, amikor az adatátalakításokhoz folyamodik. Néha csak meg kell elégednie a jelentős fejlesztésekkel. Egyébként a cselekmény azt is sugallja, hogy rendben van feltételezni, hogy a hiba varianciái egyenlőek.
a maradványok normál valószínűségi diagramja azt mutatja, hogy az x értékek átalakítása nem volt hatással a hibakifejezések normalitására:
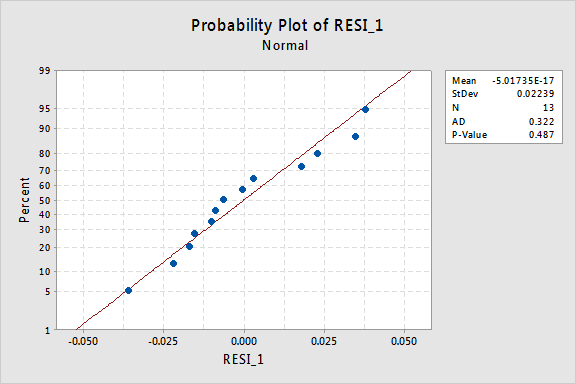
ismét az Anderson-Darling P-érték nagy, ezért nem utasítjuk el a normál hibakifejezések nullhipotézisét. Nincs elegendő bizonyíték arra a következtetésre, hogy a hibák feltételei nem normálisak.
mi lenne, ha inkább az y értékeket alakítottuk volna át? Korábban azt mondtam, hogy míg egyes feltételezések úgy tűnik, hogy tartsa alkalmazása előtt egy transzformáció, lehet, hogy már nem tart, ha egy transzformáció alkalmazzák. Például, ha a hibakifejezések jól viselkednek, az y értékek átalakítása rosszul viselkedő hibakifejezésekké változtathatja őket. Az X értékek átalakítása előtt a memória-megőrzési adatok hibakifejezései jól viselkedtek (abban az értelemben, hogy megközelítőleg normálisnak tűnnek). Ezért azt várhatjuk, hogy az y értékek átalakítása az x értékek helyett a hibakifejezések rosszul viselkedését okozhatja. Vessünk egy gyors pillantást a memória megőrzési adataira, hogy lássunk egy példát arra, hogy mi történhet az y értékek átalakításakor, amikor a nemlinearitás az egyetlen probléma.
próbával és hibával felfedezzük, hogy az Y erőátalakítása, amely a legjobb munkát végzi a nemlinearitás kijavításában, y-1.25. Az illesztett Vonaldiagram szemlélteti, hogy az átalakulás valóban kiegyenesíti a kapcsolatot — bár kétségkívül nem olyan jól, mint az X értékek log-átalakulása.
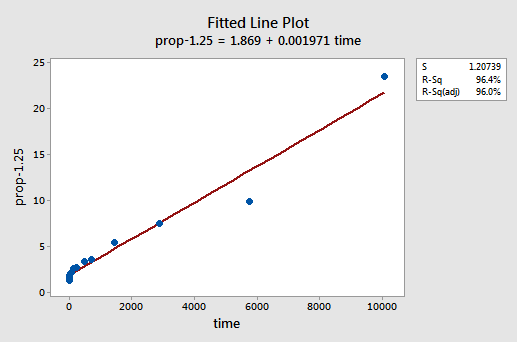
Megjegyzendő, hogy az R2 érték 57,1% – ról 96,4% – ra nőtt.
a maradványok javulást mutatnak a nemlinearitás tekintetében, bár a javulás nem nagy…
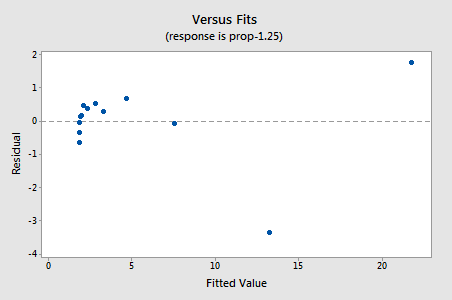
…de most nem normális hibakifejezések vannak! Az Anderson-Darling P-érték kisebb, mint 0,005, ezért elutasítjuk a normál hibakifejezések nullhipotézisét. Elegendő bizonyíték van arra, hogy a hibakifejezések nem normálisak:
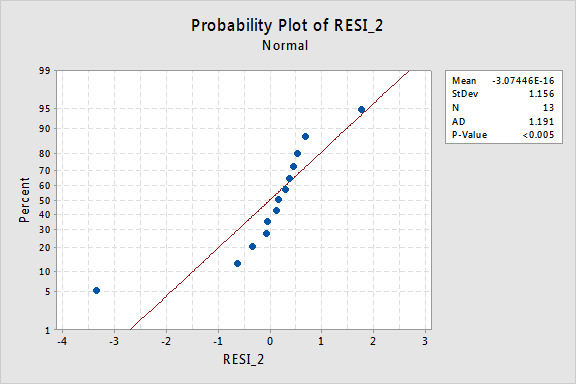
ismét, Ha a hibakifejezések jól viselkednek az átalakulás előtt, az y értékek átalakítása rosszul viselkedő hibakifejezésekké változtathatja őket.
a modell használata
miután megtaláltuk a legjobb modellt regressziós adatainkhoz, a modell segítségével válaszolhatunk érdeklődésre számot tartó kutatási kérdéseinkre. Ha modellünk transzformált prediktor (x) értékeket tartalmaz, akkor előfordulhat, hogy nem kell kisebb módosításokat végeznünk a már megtanult standard eljárásokon.
használjuk lineáris regressziós modellünket a memória—megőrzési adatokhoz—y = prop válaszként és x = lntime előrejelzőként-négy különböző kutatási kérdés megválaszolásához.
kutatási kérdés # 1: Milyen jellegű a kapcsolat a memorizálás óta eltelt idő és a visszahívás hatékonysága között?
a kutatási kérdés megválaszolásához csak leírjuk a kapcsolat jellegét. Vagyis a helyesen felidézett szavak aránya negatívan lineárisan kapcsolódik a szavak memorizálása óta eltelt idő természetes naplójához. Nem meglepő, hogy az idő természetes naplója növekszik, a visszahívott szavak aránya csökken.
2. kutatási kérdés: van-e összefüggés a memorizálás óta eltelt idő és a visszahívás hatékonysága között?
a kutatási kérdés megválaszolásához nincs szükség a szokásos eljárás módosítására. Mi csupán teszteljük a H0 nullhipotézist: 1 = 0 az F-teszt vagy az azzal egyenértékű t-teszt segítségével:
ahogy a szoftver kimenet szemlélteti, a p-érték < 0.001. Jelentős bizonyítékok vannak a 0.05 szint annak megállapítása, hogy lineáris összefüggés van a felidézett szavak aránya és a memorizálás óta eltelt idő természetes naplója között.
3. kutatási kérdés: a szavak hány százalékát várhatjuk el egy véletlenszerűen kiválasztott személytől 1000 perc elteltével?
csak ki kell számolnunk egy előrejelzési intervallumot — egy kis módosítással — a kutatási kérdés megválaszolásához. Előrejelző változónk az idő természetes naplója. Ezért, amikor statisztikai szoftvert használunk az előrejelzési intervallum kiszámításához, meg kell győződnünk arról, hogy a prediktor értékeinek értékét adjuk meg a transzformált egységekben, nem pedig az eredeti egységekben. Az 1000 perces természetes napló 6,91 log-perc. A szoftver segítségével 95% – os előrejelzési intervallumot számítunk ki, amikor lntime = 6,91, megkapjuk:
a kimenet azt mondja nekünk, hogy 95% – ban biztosak lehetünk abban, hogy a kimenet után 1000 perc alatt egy véletlenszerűen kiválasztott személy 24,5% és 35% között visszahívja.A szavak 3% – a.
4. kutatási kérdés: mennyire változik a várható visszahívás, ha az idő tízszeresére nő?
ha belegondolunk, ennek a kutatási kérdésnek a megválaszolása csupán a lejtőparaméter becslését és értelmezését foglalja magában. Nos, nem egészen—van egy kis kiigazítás. Általában az X prediktor k-szorosának növekedése a következővel jár:
cac1 ln(k)
a válasz átlagának változása y.
Ez a következő levezetés segíthet megérteni és ezért emlékezni erre a képletre.
Ez azt jelenti, hogy az x tízszeres növekedése az Y átlagának egy 1-es(10) változásához kapcsolódik. és az x kétszeres növekedése az Y átlagának 1-es(2-es) változásához kapcsolódik.
általában csak a K többszöröseit szabad használni, amelyeknek értelme van a modell hatóköréhez. Például, ha az adathalmaz x értékei 2-től 8-ig terjednek, akkor csak akkor van értelme figyelembe venni a 4 vagy annál kisebb k többszöröseket. Ha az x értéke 2 lenne, akkor tízszeres növekedés (azaz k = 10) 2-től 2-ig tartana 10 = 20, a modell hatókörén kívül eső érték. A memória-megőrzési adatkészletben az előrejelző értékek 1-től 10080-ig terjednek, így nincs probléma a tízszeres növekedés mérlegelésével.
Ha csak egy pontbecslés megszerzése érdekel minket, akkor csak a meredekség paraméterének becslését (b1 = -0.079227) vesszük a szoftver kimenetéből:

és szorozzuk meg ln(10):
B1 ++ Ln(10) = -0.079227 ++ Ln(10) = -0.182
arra számítunk, hogy a visszahívott szavak százalékos aránya csökken (mivel a jel negatív) 18.2% a memorizálás óta eltelt idő minden tízszeresére.
természetesen ez a pontbecslés korlátozott hasznosságú. Mennyire lehetünk biztosak abban, hogy a becslés közel áll a valódi ismeretlen értékhez? Természetesen ki kell számolnunk egy 95% – os magabiztos intervallumot. Ehhez csak 95% – os konfidenciaintervallumot számítunk ki a következő esetekre: 1, mint mindig: