債券を割引で売却する場合、債券割引の金額は、債券の寿命にわたって 買掛金の勘定割引の借方金額は勘定支払利息に移動されるため、償却により、各期間の支払利息は、債券が残高である各年の間に支払われた利息の額よりも大きくなります。
債券割引を償却するための好ましい方法は、実効金利法または実効金利法です。 実効金利法では、特定の会計期間における支払利息の額は、会計期間の開始時の債券の簿価の額と相関します。 これは、債券の簿価が増加するにつれて、支払利息の量が増加することを意味します。
私たちは5年9%bond100,000のための10%の市場で発行された債券の実効金利法を実証する前に9 96,149、のは、いくつかのポイントを強調してみましょう:
-
3,851ドルの債券割引は、債券の寿命にわたって支払利息に償却する必要があります。 償却により、債券の簿価は、2019年1月1日の96,149ドルから、2023年12月31日に満期になる直前の100,000ドルに増加します。
-
企業は、債券が残高であることを各June30とDecember31にinterest4,500(1 100,000×9%x6/12)の利息の支払いを行う必要があります。 現金口座は、これらの日付のそれぞれにcredited4,500のために入金されます。
-
実効金利は、債券が発行された日の市場金利です。 この例では、2019年1月1日の市場金利は、10半期の半期ごとに5%でした。
-
実効金利は、会計期間の開始時に債券の簿価に乗算され、各期間の支払利息に到達します。
-
項目2と項目4の違いは償却額です。
次の表は、買掛金のbonds3,851割引を償却する実効金利方法を示しています。
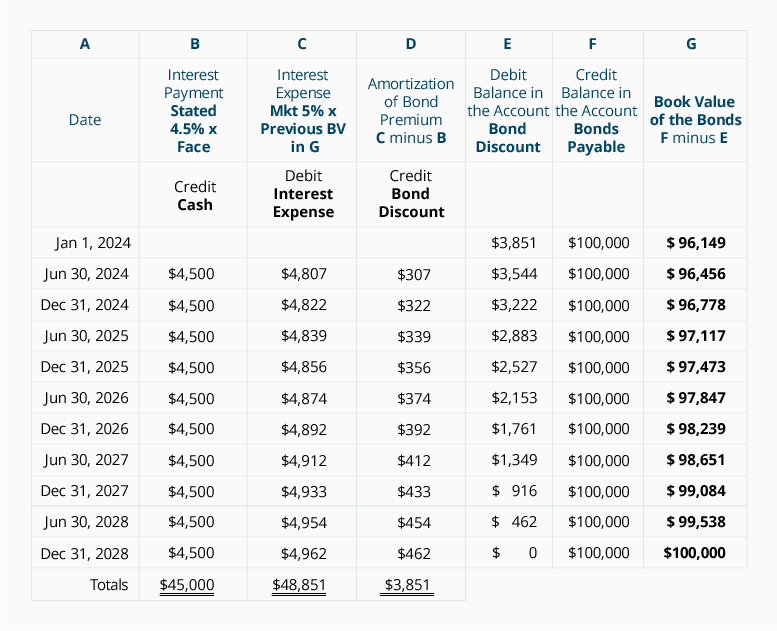
上記の表についていくつかのポイントを作ってみましょう。
-
列Bは、債券契約に必要な利払いを示しています。年間9%を半年=4.5%で割った債券のレートを示しています。半年ごとの期間ごとに結合の顔の量を倍に掛けました。
-
列Cは支払利息を示しています。 この計算は、債券が発行された時点での市場金利を使用しています: 2つの半期で割った年間10%の市場率=5%半期。
-
列Cの支払利息は、半期あたりの5%の市場金利と半期の開始時の債券の簿価の積です。 利息費用と債券の簿価との間のこの相関関係は、有効金利法を、買掛金の割引を償却するための好ましい方法にしています。
-
使用した現在価値係数は小数点以下三桁に四捨五入されていたため、コンピュータソフトウェア、金融電卓、または小数点以下の桁数に実行された係数の使用によって決定された金額ほど正確ではありません。 その結果、2023年の償却額は若干の調整が必要となりました。
当社が年次財務諸表のみを発行し、会計年度が31日に終了した場合、上記のスケジュールの金額を使用して、債券割引の償却を利息支払日に記録す この例では、債券は6月30日と12月31日に利息を支払うため、債券の発行日と各会計年度の終わりに未収利息はありません。 債券発行を記録するためのエントリを含む2019年のエントリは、次のように示されています。
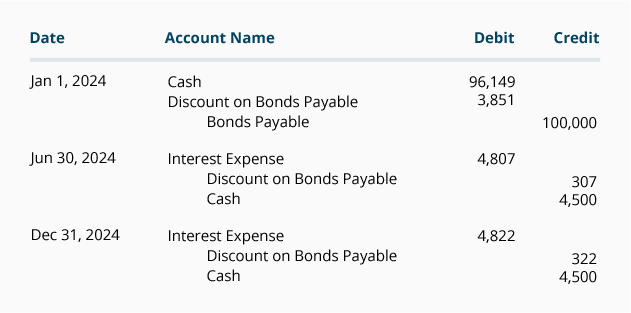
2020年の仕訳エントリは次のとおりです。

2021年から2023年の仕訳エントリも上記のスケジュールから取得されます。
償却方法の比較
以下は、実効金利法および定額法における支払利息の額の比較です。 実効金利法では、債券の簿価が増加するにつれて、毎年の支払利息が増加していることに注意してください。 定額法では、債券の簿価が増加しているにもかかわらず、支払利息は一定の金額にとどまります。 会計専門家は、実効金利法を好むが、債券割引の量が有意でない場合には、定額法を可能にする。
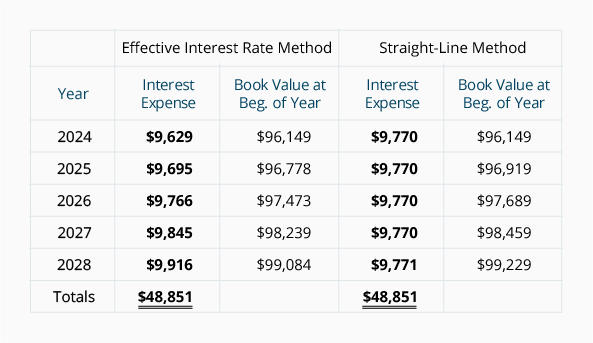
償却の両方の方法の下で、債券が発行された時点で簿価($96,149)はbond100,000の債券の満期値に向かって移動することに注意してください。 その理由は、債券割引が支払利息に償却されるため、bond3,851の債券割引が0 0に減少しているためです。
また、両方の方法の下で債券の寿命にわたる総支払利息は$48,851(利息の支払いのplus45,000プラス債券割引の3 3,851であることに注意してください。
また、)
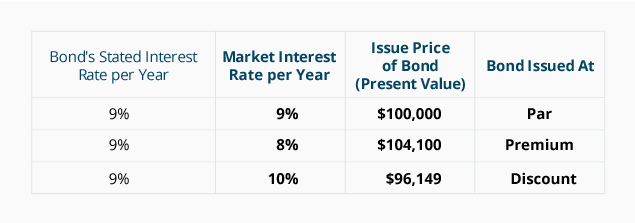
市場金利が債券発行価格に及ぼす影響の概要
次の表は、100,000ドルの既存の債券に対する市場金利の変化の影響をまとめたもので、金利が9%で5年後に満期となる。p>