このセクションでは、予測子x値を変換することにより、単純な線形回帰モデ これは、データに非線形傾向が見つかった場合に最初に試すことができます。 つまり、非線形性が唯一の問題である場合(つまり、独立性、正規性、および等分散の条件が満たされている場合)、x値の変換が適切です。 ただし、正規性と等分散の仮定を評価する前に、非線形性を修正する必要がある場合があることに注意してください。 また、一部の仮定は、変換を適用する前に保持されるように見えるかもしれませんが、変換が適用されると保持されなくなる可能性があります。 つまり、変換を使用することは、すべての線形回帰の仮定が各反復後に再チェックされる反復プロセスの一部です。
ここでは単純な線形回帰モデルに焦点を当てていますが、本質的なアイデアはより一般的に多重線形回帰モデルにも適用されることに注意し 残差の散布図と各予測子を順番に調べることによって、任意の予測子を変換することを検討できます。
モデルを構築する
例を示します。 データ変換について学ぶ最も簡単な方法は例です。 13人の被験者が切断された項目のリストを記憶するように求められた記憶保持実験からのデータを考えてみましょう。 被験者はその後、一週間後まで様々な時間にアイテムをリコールするように求められました。 リストが記憶されて以来、さまざまな時間(x=時間、分単位)で正しくリコールされた項目(y=prop)の割合が記録されました(wordrecall。txt)とプロットされている。 誤差項が独立していないという正当な理由がないことを認識して、モデルの残りの3つの条件(線形性、正規性、および等分散)を評価しましょう。
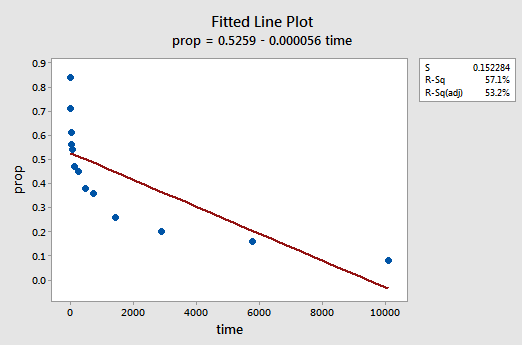
結果として得られる近似折れ線プロットは、リコールされた項目の割合(y)が時間(x)に線形に関連していないことを示唆しています。
結果の近似折れ線:
残差対フィットプロットは、関係が線形ではないことを示唆しています。
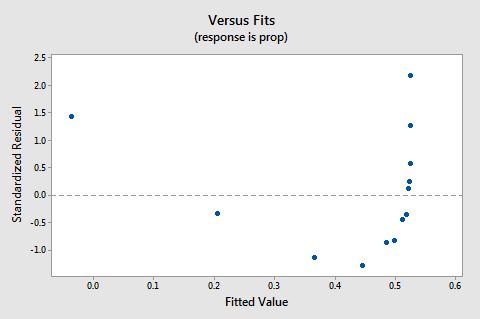



線形性の欠如がプロットを支配するため、誤差分散が等しいかどうかを評価するためにプロットを使用することはできません。 等分散の仮定を評価する前に、非線形性の問題を修正する必要があります。残差の正規確率プロットはどうですか?
エラー用語については何を示唆していますか? 彼らは正規分布していると結論づけることができますか?
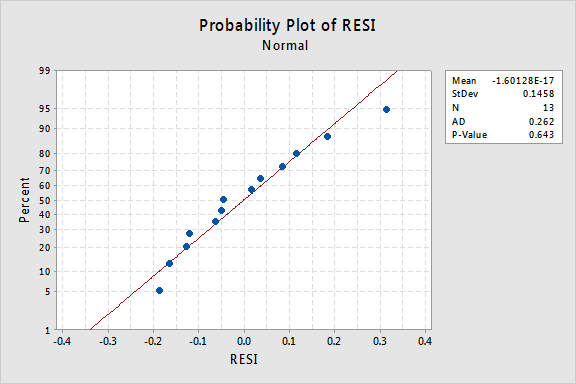
この例のAnderson-Darling P値は0.643であり、正規誤差項の帰無仮説を棄却できないことを示唆しています。 エラー項が正常でないと結論づけるのに十分な証拠はありません。要約すると、非線形性が唯一の主要な問題であるデータセットがあります。 この状況は、予測子の値のみを変換するために悲鳴を上げます。 これを行う前に、「対数変換」は利用可能な最も一般的で最も有用なデータ変換であるため、脇に置いて「対数変換」について説明しましょう。
対数変換。 デフォルトの対数変換には、各データ値の自然対数(lnまたはloge、または単にlog)を使用するだけです。 10を底とする対数や2を底とする対数など、異なる種類の対数を取ることを検討することができます。 しかし、自然対数-これは対数底eと考えることができます。eは定数2.718282です。.. -科学的な仕事で使用される最も一般的な対数スケールです。
自然対数関数の一般的な特性は次のとおりです。
- xの自然対数はe=2.718282のべき乗です。
- xの自然対数はe=2.718282のべき乗です。
- .. たとえば、5の自然対数は、e=2.718282を上げなければならないべき乗です。xを得るためには、これを取る必要があります。ln(ex)=xと表記することができます。.. 5を取得するために。 2.7182821.60944は約5であるため、5の自然対数は1.60944であると言います。 記法的には、ln(5)=1.60944と言います。
- eの自然対数は1に等しい、つまりln(e)=1です。
- 1の自然対数はゼロに等しい、つまりln(1)=0です。
自然対数関数のプロット:
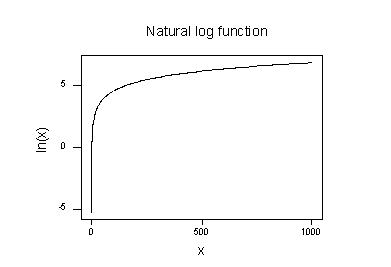
自然対数変換を取ることの効果は次のとおりであることを示唆しています。
- 広がっている大きな値は、一緒に近づいています。
この例に戻ります。 自然対数を使用して、メモリ保持実験データのx値を変換しましょう。 X=timeは予測子なので、データセットに表示される各時間値の自然対数を取るだけです。 そうすることで、lntimeと呼ばれる新しく変換された予測変数を作成します。
time prop time prop 0.84 0.84 0.84 1 0.84 0.84 0.84 5 0.71 1.60944 15 0.61 2.70805 30 0.56 3.40120 60 0.54 4.09434 120 0.47 4.78749 240 0.45 5.48064 480 0.38 6.17379 720 0.36 6.57925 1440 0.26 7.27240 2880 0.20 7.96555 5760 0.16 8.65869 10080 0.08 9.21831 We take the natural logarithm for each value of time and place the results in their own column. つまり、各予測子時間値をln(時間)値に「変換」します。 たとえば、ln(1)=0、ln(5)=1.60944、ln(15)=2.70805などです。予測値を変換したので、データ内の非線形傾向を修正するのに役立つかどうかを見てみましょう。
予測値を変換したので、データ内の非線形傾向を修正するのに役立つかどうかを見てみましょう。 応答としてy=prop、予測子としてx=lntimeを使用してモデルを再近似します。
結果の近似折れ線プロットは、予測子値の自然対数を取ることが有用であることを示唆しています。
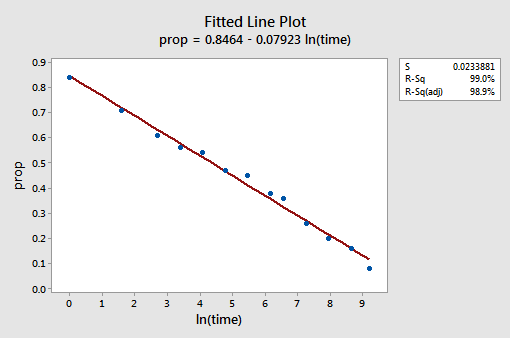
確かに、R2値は57.1%から99.0%に増加しました。 それは、リコールされた単語(prop)の割合の変動の99%が時間の自然対数(lntime)を考慮に入れることによって減少することを教えてくれます!
新しい残差対fitsプロットは、変換されていないデータに基づくものよりも大幅に改善されています。
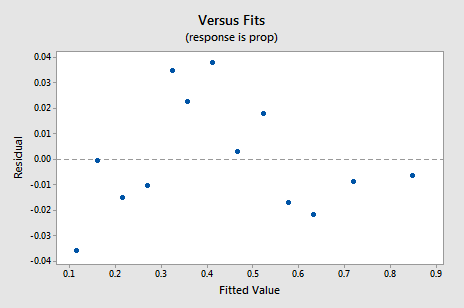
プロット内のある種のアップダウン循環傾向が心配になるかもしれません。 特にデータセットがこのように小さい場合は、これらのプロットを過度に解釈しないように再度注意してください。 あなたがデータ変換を取ることに頼るとき、あなたは本当に完璧を期待すべきではありません。 時には、あなただけの大幅な改善に満足している必要があります。 ちなみに、このプロットは、誤差分散が等しいと仮定しても大丈夫であることも示唆しています。
残差の正規確率プロットは、x値の変換が誤差項の正規性に影響を与えなかったことを示しています:
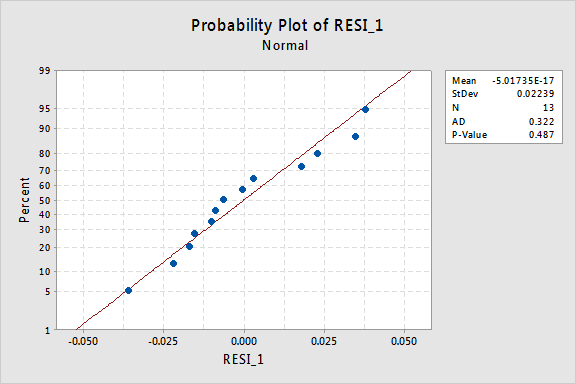
再びAnderson-Darling P値が大きいので、正規誤差項の帰無仮説を棄却することはできません。 エラー項が正常でないと結論づけるのに十分な証拠はありません。代わりにy値を変換した場合はどうなりますか?
以前、私は、変換を適用する前にいくつかの仮定が保持されているように見えるかもしれませんが、変換が適用されると保持されなくなる可能性が たとえば、誤差項が正常に動作している場合、y値を変換すると、それらが正常に動作していない誤差項に変更される可能性があります。 X値を変換する前のメモリ保持データのエラー項は、(ほぼ正常に見えるという意味で)正常に動作しているように見えます。 したがって、x値の代わりにy値を変換すると、エラー項が正しく動作しなくなる可能性があることが予想される場合があります。 メモリ保持データを簡単に見て、非線形性が唯一の問題であるときにy値を変換するときに何が起こるかの例を見てみましょう。試行錯誤して、非線形性を補正するのに最適なyのべき乗変換がy-1.25であることを発見しました。
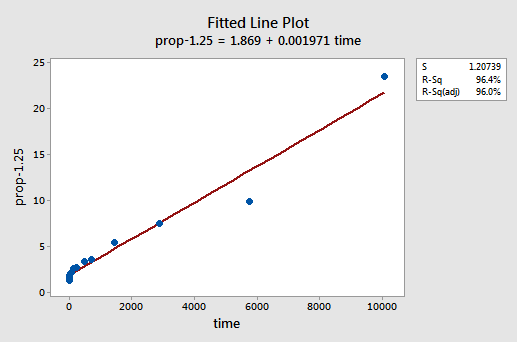
R2値が57.1%から96.4%に増加したことに注意してください。
残差は非線形性に関して改善を示しますが、改善は大きくありません。..
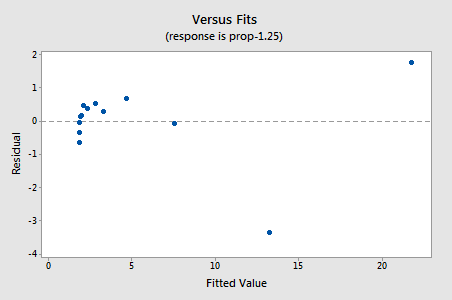
。..しかし、今、私たちは非通常のエラー用語を持っています! Anderson-DarlingのP値は0.005未満であるため、正規誤差項の帰無仮説を棄却します。 エラー項が正常ではないと結論づけるのに十分な証拠があります。
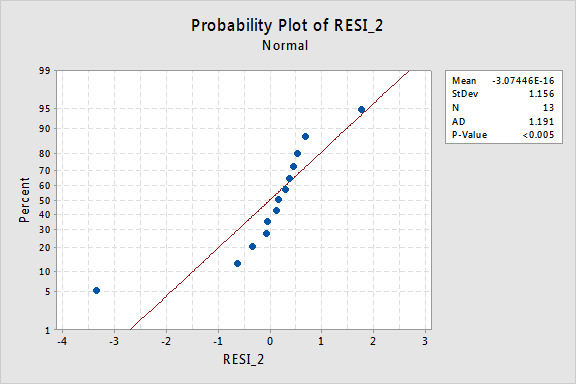
ここでも、エラー項が変換前に正常に動作している場合、y値を変換すると、それらを悪い動作のエラー項に変更することができます。
モデルの使用
回帰データに最適なモデルが見つかったら、そのモデルを使用して関心のある研究の質問に答えることができます。 モデルに変換された予測子(x)値が含まれている場合、既に学習した標準手順にわずかな変更を加える必要がある場合とそうでない場合があります。4つの異なる研究の質問に答えるために、y=propを応答として、x=lntimeを予測子として、メモリ保持データに線形回帰モデルを使用しましょう。
: 記憶されてからの時間とリコールの有効性との間の関連性の性質は何ですか?

この研究の質問に答えるために、我々はちょうど関係の性質 つまり、正しくリコールされた単語の割合は、単語が記憶されてからの時間の自然対数に負に線形に関連しています。 当然のことながら、時間の自然対数が増加するにつれて、リコールされた単語の割合は減少する。研究の質問#2:記憶されてからの時間とリコールの有効性との間に関連性はありますか?
この研究の質問に答えるには、標準的な手順を変更する必要はありません。
帰無仮説h0:β1=0をF検定または同等のt検定のいずれかを使用して検定するだけです。
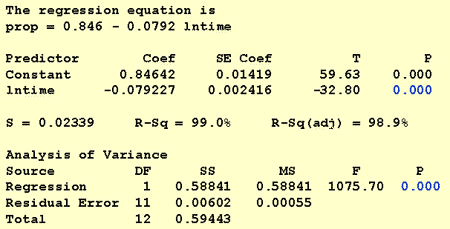
ソフトウェア出力が示すように、p値は
<0.001. 0には重要な証拠があります。05レベルは、想起された単語の割合と記憶されてからの時間の自然対数との間に線形関連があると結論づける。研究の質問#3:ランダムに選択された人が1000分後に思い出すと、どの割合の単語が期待できますか?
この研究の質問に答えるには、わずかな変更を加えて予測間隔を計算するだけです。
この研究の質問に答えるには、予測間隔を計算するだけです。
私たちの予測変数は、時間の自然対数です。 したがって、統計ソフトウェアを使用して予測区間を計算するときは、元の単位ではなく、変換された単位で予測子値の値を指定する必要があります。 1000分の自然対数は6.91log-minutesです。 ソフトウェアを使用して、lntime=6.91のときに95%の予測間隔を計算すると、次のようになります。

出力は、1000分後に無作為に選択された人が95%自信を持つことができることを示しています。24.5%から35%の間でリコールされます。言葉の3%。研究の質問#4:時間が十倍に増加した場合、予想されるリコールはどのくらい変化しますか?
あなたがそれについて考えるならば、この研究の質問に答えることは単に勾配パラメータβ1を推定して解釈することを含みます。 まあ、かなりではない—わずかな調整があります。 一般に、予測子xのk倍の増加は、aに関連付けられます。
β1×ln(k)
応答yの平均の変化。
次のこの導出は、この式を理解し、覚えておくのに役立ち
つまり、xの十倍の増加は、yの平均のβ1×ln(10)変化に関連付けられています。xの二倍の増加は、yの平均のβ1×ln(2)変化に関連付けられています。
一般に、モデルの範囲に意味のあるkの倍数のみを使用する必要があります。 たとえば、データセットのx値が2から8の範囲である場合、4以下のk倍数を考慮することは理にかなっています。 Xの値が2の場合、10倍の増加(つまり、k=10)は、2から2×10=20まで、モデルの範囲外の値になります。 メモリ保持データセットでは、予測子値の範囲は1~10080であるため、10倍の増加を考慮しても問題はありません。点推定値のみを求める場合は、ソフトウェア出力から傾きパラメータの推定値(b1=-0.079227)を取得します。

それにln(10)を掛けます。
b1×ln(10)を乗算します。
b1×ln(10)を乗算します。
b1×ln(10)を乗算します。
b1×ln(10)を乗算します。
b1×ln(10)を乗算します。
10)=-0.079227×ln(10)=-0.182
リコールされた単語の割合が減少すると予想されます(符号が負であるため)18。暗記が行われてからの時間の各十倍の増加のための2%。
もちろん、この点の推定値は限られた有用性のものです。 推定値が真の未知の値に近いことをどのように確信できますか? 当然のことながら、95%の信頼区間を計算する必要があります。 これを行うには、常に次のようにβ1の95%信頼区間を計算します。
- xの自然対数はe=2.718282のべき乗です。