In deze sectie leren we hoe we een eenvoudig lineair regressiemodel kunnen bouwen en gebruiken door de predictor x-waarden te transformeren. Dit kan het eerste zijn dat je probeert als je een niet-lineaire trend in je gegevens vindt. Dat wil zeggen, het transformeren van de x-waarden is geschikt wanneer niet-lineariteit het enige probleem is (dat wil zeggen, de onafhankelijkheid, normaliteit, en gelijke variantie voorwaarden zijn voldaan). Merk echter op dat het nodig kan zijn om de niet-lineariteit te corrigeren voordat u de normaliteit en gelijke variantie veronderstellingen kunt beoordelen. Hoewel sommige aannames lijken te gelden voordat een transformatie wordt toegepast, kunnen ze ook niet langer gelden zodra een transformatie wordt toegepast. Met andere woorden, het gebruik van transformaties maakt deel uit van een iteratief proces waarbij alle lineaire regressieaannames na elke iteratie opnieuw worden gecontroleerd.
Houd er rekening mee dat hoewel we ons hier richten op een eenvoudig lineair regressiemodel, de essentiële ideeën meer in het algemeen ook van toepassing zijn op meerdere lineaire regressiemodellen. We kunnen overwegen om een van de voorspellers te transformeren door de verstrooiing van de reststoffen te onderzoeken ten opzichte van elke voorspeller op zijn beurt.
bouwen van het model
een voorbeeld. De makkelijkste manier om te leren over data transformaties is door voorbeeld. Laten we eens kijken naar de gegevens van een geheugen retentie experiment waarin 13 proefpersonen werden gevraagd om een lijst van losgekoppelde items onthouden. De proefpersonen werden vervolgens gevraagd om de items op verschillende tijdstippen tot een week later terug te roepen. De verhouding van de items (y = prop) correct teruggeroepen op verschillende tijdstippen (x = tijd, in minuten) sinds de lijst werd gememoriseerd werden geregistreerd (wordrecall.txt) en uitgezet. Erkennend dat er geen goede reden is dat de fout termen niet onafhankelijk zouden zijn, laten we de resterende drie voorwaarden — lineariteit, normaliteit, en gelijke varianties — van het model evalueren.
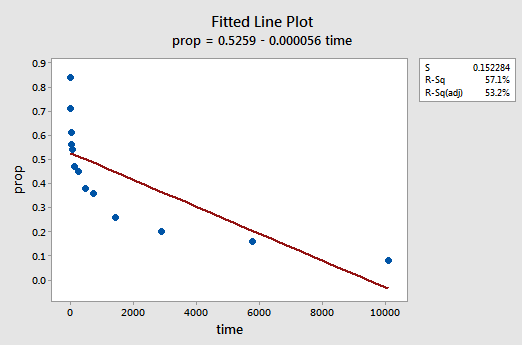
het resulterende ingerichte lijnperceel suggereert dat het aandeel van teruggeroepen items (y) niet lineair gerelateerd is aan de tijd (x):
De residuals vs fits-plot suggereert ook dat de relatie niet lineair is:
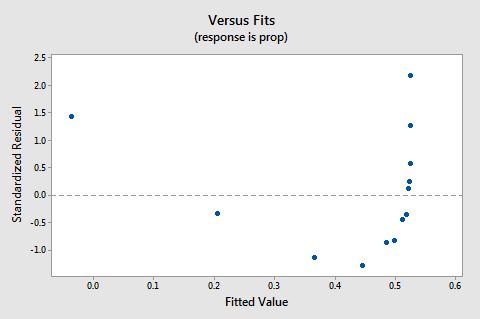
omdat het gebrek aan lineariteit de plot domineert, kunnen we de plot niet gebruiken om te beoordelen of de foutvarianties gelijk zijn of niet. We moeten het probleem van de niet-lineariteit oplossen voordat we de aanname van gelijke varianties kunnen beoordelen.
hoe zit het met de normale kansberekening van de reststoffen? Wat suggereert het over de fout termen? Kunnen we concluderen dat ze normaal worden verspreid?
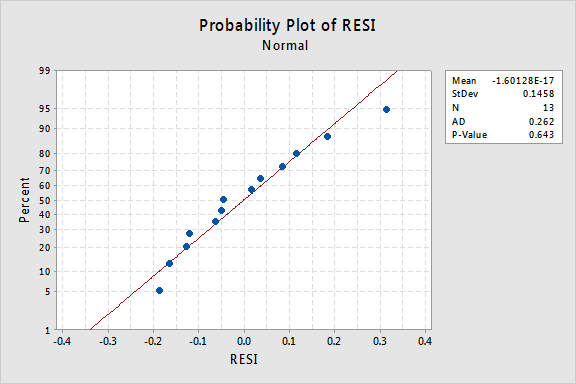
De Anderson-Darling P-waarde voor dit voorbeeld is 0,643, wat suggereert dat we de nulhypothese van normale fouttermen niet kunnen afwijzen. Er is niet genoeg bewijs om te concluderen dat de termen fouten niet normaal zijn.
samengevat hebben we een gegevensverzameling waarin niet-lineariteit het enige grote probleem is. Deze situatie schreeuwt om het transformeren van alleen de waarden van de voorspeller. Voordat we dit doen, laten we een apart nemen en bespreken de “logaritmische transformatie,” omdat het de meest voorkomende en meest bruikbare data transformatie beschikbaar is.
de logaritmische transformatie. De standaard logaritmische transformatie omvat slechts het nemen van de natuurlijke logaritme — aangeduid ln of loge of gewoon log — van elke Data waarde. Men zou kunnen overwegen om een ander soort logaritme te nemen, zoals log base 10 of log base 2. Echter, de natuurlijke logaritme – die kan worden beschouwd als log base e waar e is de constante 2.718282… – is de meest voorkomende logaritmische schaal gebruikt in wetenschappelijk werk.
de Algemene kenmerken van de natuurlijke logaritmische functie zijn:
- de natuurlijke logaritme van x is de macht van e = 2.718282… dat je moet nemen om x te krijgen. dit kan notioneel worden gesteld als ln (ex) = x. bijvoorbeeld, de natuurlijke logaritme van 5 is de macht waartoe je e = 2.718282 moet verhogen… om 5 te krijgen. Aangezien 2.7182821.60944 ongeveer 5 is, zeggen we dat de natuurlijke logaritme van 5 1,60944 is. Notatie, zeggen we ln (5) = 1.60944.
- de natuurlijke logaritme van e is gelijk aan één, dat wil zeggen ln(e) = 1.
- de natuurlijke logaritme van één is gelijk aan nul, dat wil zeggen, ln (1) = 0.
de plot van de natuurlijke logaritmische functie:
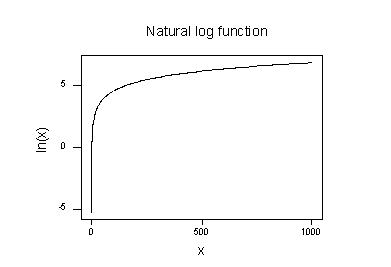
suggereert dat de effecten van het nemen van de natuurlijke logaritmische transformatie zijn:
- kleine waarden die dicht bij elkaar liggen, worden verder uitgespreid.
- Grote waarden die worden uitgespreid, worden dichter bij elkaar gebracht.
terug naar het voorbeeld. Laten we de natuurlijke logaritme gebruiken om de x-waarden in de geheugenretentie experiment data te transformeren. Aangezien x = tijd de voorspeller is, hoeven we alleen maar de natuurlijke logaritme te nemen van elke tijdwaarde die in de dataset voorkomt. In dit te doen, creëren we een nieuw getransformeerd voorspeller genoemd lntime:
| tijd | prop | lntime |
| 1 | 0.84 | 0.00000 |
| 5 | 0.71 | 1.60944 |
| 15 | 0.61 | 2.70805 |
| 30 | 0.56 | 3.40120 |
| 60 | 0.54 | 4.09434 |
| 120 | 0.47 | 4.78749 |
| 240 | 0.45 | 5.48064 |
| 480 | 0.38 | 6.17379 |
| 720 | 0.36 | 6.57925 |
| 1440 | 0.26 | 7.27240 |
| 2880 | 0.20 | 7.96555 |
| 5760 | 0.16 | 8.65869 |
| 10080 | 0.08 | 9.21831 |
We take the natural logarithm for each value of time and place the results in their own column. Dat wil zeggen, we “transformeren” elke voorspeller tijdwaarde naar een ln (Tijd) Waarde. Bijvoorbeeld ln (1) = 0, ln(5) = 1.60944, en ln(15) = 2.70805, enzovoort.
nu we de waarden van de voorspeller hebben getransformeerd, laten we eens kijken of het hielp de niet-lineaire trend in de gegevens te corrigeren. We passen het model opnieuw aan met y = prop als respons en x = lntime als voorspeller.
de resulterende ingerichte lijn plot suggereert dat het nemen van de natuurlijke logaritme van de voorspeller waarden nuttig is.
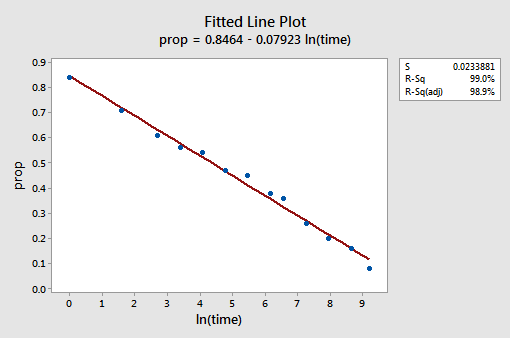
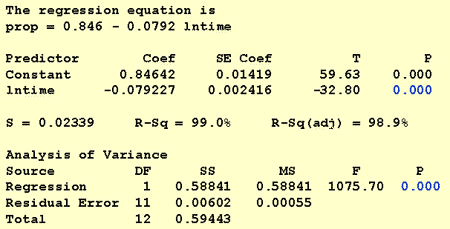
De R2-waarde is inderdaad gestegen van 57,1% naar 99,0%. Het vertelt ons dat 99% van de variatie in de verhouding van de teruggeroepen woorden (prop) wordt verminderd door rekening te houden met de natuurlijke log van de tijd (lntime)!
de nieuwe residuele vs.fits-grafiek toont een significante verbetering ten opzichte van de grafiek gebaseerd op de niet-getransformeerde gegevens.
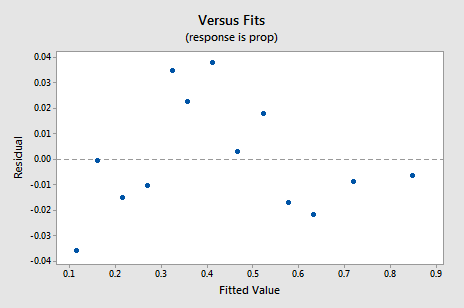
u kunt zich zorgen maken over een opwaartse cyclische trend in de plot. Ik waarschuw u nogmaals om deze plots niet te veel te interpreteren, vooral als de dataset zo klein is. Je moet echt niet perfectie verwachten wanneer je toevlucht neemt tot het nemen van data transformaties. Soms moet je gewoon tevreden zijn met belangrijke verbeteringen. Trouwens, de plot suggereert ook dat het goed is om aan te nemen dat de foutvarianties gelijk zijn.
de normale waarschijnlijkheidsplanning van de reststoffen laat zien dat de omzetting van de x-waarden geen effect had op de normaliteit van de fouttermen:
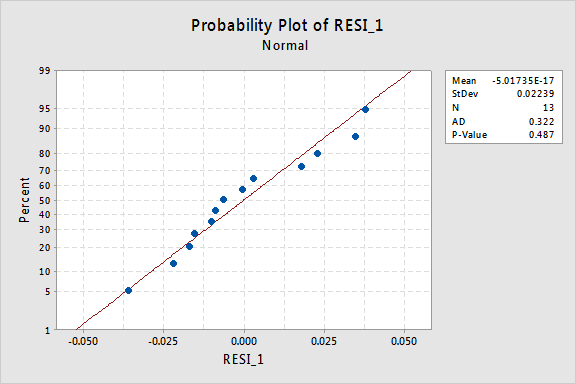
opnieuw is de Anderson-Darling P-waarde groot, dus we kunnen de nulhypothese van normale fouttermen niet afwijzen. Er is niet genoeg bewijs om te concluderen dat de termen fouten niet normaal zijn.
Wat als we in plaats daarvan de Y-waarden hadden getransformeerd? Eerder zei ik dat hoewel sommige veronderstellingen kunnen lijken te houden voorafgaand aan het toepassen van een transformatie, ze kunnen niet langer houden als een transformatie wordt toegepast. Bijvoorbeeld, als de fouttermen goed gedragen zijn, kan het transformeren van de y-waarden ze veranderen in slecht gedragen fouttermen. De fouttermen voor de geheugenretentiegegevens voorafgaand aan het transformeren van de x-waarden lijken goed gedragen te zijn (in de zin dat ze ongeveer normaal lijken). Daarom kunnen we verwachten dat het transformeren van de y-waarden in plaats van de x-waarden ervoor kan zorgen dat de fouttermen zich slecht gedragen. Laten we eens een snelle blik op de geheugenretentie gegevens om een voorbeeld van wat er kan gebeuren als we transformeren de y-waarden wanneer niet-lineariteit is het enige probleem te zien.
door trial and error, ontdekken we dat de machtstransformatie van y die het beste werk doet bij het corrigeren van de niet-lineariteit y-1,25 is. De ingerichte lijn plot illustreert dat de transformatie inderdaad rechttrekken van de relatie — hoewel toegegeven niet zo goed als de log transformatie van de x-waarden.
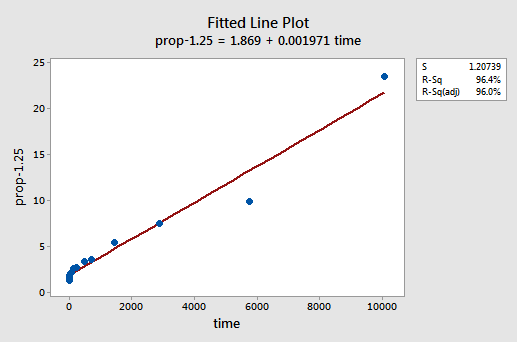
merk op dat de R2-waarde is gestegen van 57,1% tot 96,4%.
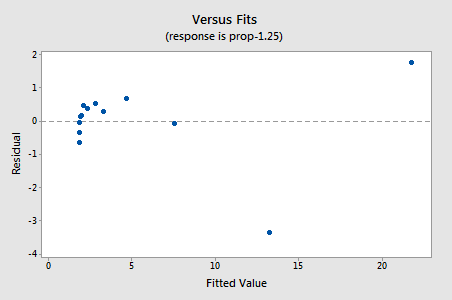
de reststoffen vertonen een verbetering ten opzichte van niet-lineariteit, hoewel de verbetering niet groot is…
…maar nu hebben we niet-normale fout termen! De Anderson-Darling P-waarde is minder dan 0,005, dus we verwerpen de nulhypothese van normale fouttermen. Er is voldoende bewijs om te concluderen dat de fouttermen niet normaal zijn:
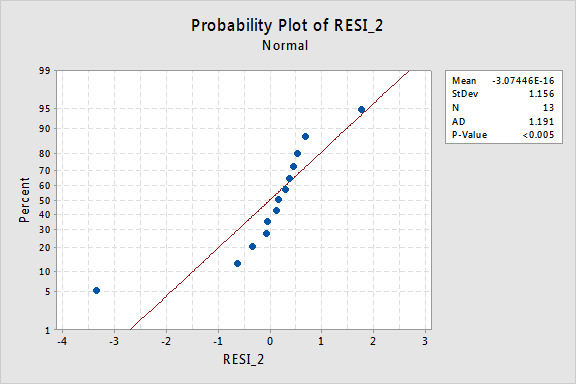
nogmaals, als de fouttermen zich goed gedragen voorafgaand aan de transformatie, kan het transformeren van de y-waarden ze veranderen in fouttermen die zich slecht gedragen.
met behulp van het model
zodra we het beste model voor onze regressiegegevens hebben gevonden, kunnen we het model gebruiken om onze onderzoeksvragen te beantwoorden. Als Ons model getransformeerde predictor (x) waarden bevat, hoeven we misschien wel of niet kleine wijzigingen aan te brengen in de standaard procedures die we al hebben geleerd.
laten we ons lineaire regressiemodel gebruiken voor de geheugenretentiegegevens—met y = prop als respons en x = lntime als voorspeller—om vier verschillende onderzoeksvragen te beantwoorden.
onderzoeksvraag # 1: Wat is de aard van de associatie tussen de tijd sinds gememoriseerd en de effectiviteit van recall?
om deze onderzoeksvraag te beantwoorden, beschrijven we de aard van de relatie. Dat wil zeggen, de verhouding van correct herinnerde woorden is negatief lineair gerelateerd aan de natuurlijke log van de tijd sinds de woorden werden onthouden. Niet verrassend, als de natuurlijke log van de tijd toeneemt, neemt het aandeel van de herinnerde woorden af.
onderzoeksvraag # 2: is er een verband tussen tijd sinds gememoriseerd en effectiviteit van recall?
bij het beantwoorden van deze onderzoeksvraag is geen wijziging van de standaardprocedure nodig. We testen alleen de nulhypothese H0: β1 = 0 met behulp van de F-test of de equivalente t-test:
zoals de softwareuitvoer illustreert, is de p-waarde < 0,001. Er is significant bewijs bij de 0.05 niveau om te concluderen dat er een lineaire associatie is tussen de verhouding van woorden die worden herinnerd en de natuurlijke log van de tijd die sindsdien is onthouden.
onderzoeksvraag # 3: hoeveel woorden kunnen we verwachten dat een willekeurig gekozen persoon zich na 1000 minuten herinnert?
We hoeven alleen maar een voorspellingsinterval te berekenen – met één kleine wijziging-om deze onderzoeksvraag te beantwoorden. Onze voorspellende variabele is de natuurlijke log van de tijd. Daarom, wanneer we statistische software gebruiken om het voorspellingsinterval te berekenen, moeten we ervoor zorgen dat we de waarde van de voorspellende waarden in de getransformeerde eenheden specificeren, niet de oorspronkelijke eenheden. De natuurlijke log van 1000 minuten is 6,91 log-minuten. Met behulp van software om een 95% voorspellingsinterval te berekenen wanneer lntime = 6.91, verkrijgen we:
De output vertelt ons dat we 95% zeker kunnen zijn dat, na 1000 minuten, een willekeurig geselecteerde persoon zich tussen 24,5% en 35.3% van de woorden.
onderzoeksvraag # 4: hoeveel verandert de verwachte recall als de tijd vertienvoudigt?
als je erover nadenkt, is het beantwoorden van deze onderzoeksvraag slechts het schatten en interpreteren van de helling parameter β1. Nou, niet helemaal – er is een kleine aanpassing. In het algemeen wordt een K-voudige toename in de voorspeller x geassocieerd met a:
β1 × ln(k)
verandering in het gemiddelde van de respons y.
deze afleiding die volgt kan u helpen deze formule te begrijpen en te onthouden.
dat wil zeggen, een tienvoudige toename in x wordt geassocieerd met een β1 × ln(10) verandering in het gemiddelde van y. en, een tweevoudige toename in x wordt geassocieerd met een β1 × ln(2) verandering in het gemiddelde van y.
in het algemeen moet u alleen veelvouden van k gebruiken die zinvol zijn voor de reikwijdte van het model. Bijvoorbeeld, als de x-waarden in uw dataset variëren van 2 tot 8, is het alleen zinvol om K-veelvouden te beschouwen die 4 of kleiner zijn. Als de waarde van x 2 was, zou een tienvoudige toename (d.w.z. k = 10) je van 2 tot 2 × 10 = 20 brengen, een waarde die buiten het kader van het model valt. In de geheugenretentie dataset variëren de waarden van de voorspeller van 1 tot 10080, dus er is geen probleem met het overwegen van een tienvoudige toename.
Als we alleen geïnteresseerd zijn in het verkrijgen van een puntschatting we alleen nemen de schatting van de helling parameter (b1 = -0.079227) van de software output:

en vermenigvuldigen met ln(10):
b1 × ln(10) = -0.079227 × ln(10) = -0.182
We verwachten dat het percentage van herinnerd aan de woorden te verlagen (omdat het teken is negatief) 18.2% voor elke tienvoudige toename in de tijd sinds het onthouden plaatsvond.
natuurlijk is deze puntschatting van beperkt nut. Hoe Zeker kunnen we zijn dat de schatting dicht bij de echte onbekende waarde ligt? Natuurlijk moeten we een 95% betrouwbaarheidsinterval berekenen. Hiervoor berekenen we gewoon een 95% betrouwbaarheidsinterval voor β1 zoals we altijd hebben: