w tej sekcji nauczymy się budować i używać prostego modelu regresji liniowej poprzez przekształcenie wartości predictor x. To może być pierwsza rzecz, którą spróbujesz, jeśli znajdziesz nieliniowy trend w swoich danych. Oznacza to, że przekształcenie wartości x jest właściwe, gdy Nieliniowość jest jedynym problemem (tj. spełnione są warunki niezależności, normalności i równej wariancji). Należy jednak pamiętać, że może być konieczne skorygowanie nieliniowości, zanim będzie można ocenić założenia normalności i równej wariancji. Ponadto, podczas gdy niektóre założenia mogą wydawać się posiadać przed zastosowaniem transformacji, mogą one już nie posiadać po zastosowaniu transformacji. Innymi słowy, wykorzystanie przekształceń jest częścią procesu iteracyjnego, w którym wszystkie założenia regresji liniowej są ponownie sprawdzane po każdej iteracji.
pamiętaj, że chociaż skupiamy się tutaj na prostym modelu regresji liniowej, zasadnicze idee odnoszą się bardziej ogólnie do wielu modeli regresji liniowej. Możemy rozważyć przekształcenie dowolnego z predyktorów, badając rozrzuty pozostałości w porównaniu z każdym predyktorem po kolei.
budowa modelu
przykład. Najprostszym sposobem na poznanie transformacji danych jest przykład. Rozważmy dane z eksperymentu retencji pamięci, w którym 13 osób zostało poproszonych o zapamiętywanie listy odłączonych elementów. Badani zostali następnie poproszeni o przypomnienie sobie przedmiotów w różnych okresach, aż do tygodnia później. Rejestrowano proporcje elementów (y = prop) poprawnie przywołanych w różnych momentach (x = czas, w minutach) od zapamiętania listy (wordrecall.txt) i wykreślone. Uznając, że nie ma dobrego powodu, aby terminy błędów nie były niezależne, ocenimy pozostałe trzy warunki — liniowość, normalność i równe wariancje — modelu.
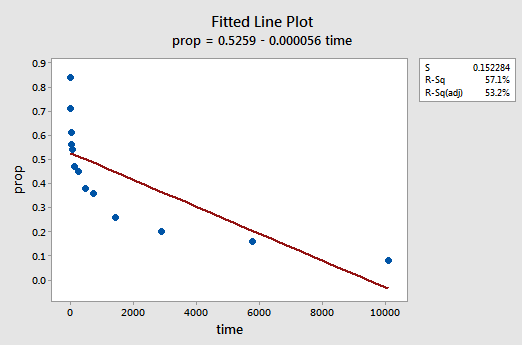
uzyskany wykres liniowy sugeruje, że proporcja elementów (y) nie jest liniowo związana z czasem (x):
Wykres residuals vs fits sugeruje również, że relacja nie jest liniowa:
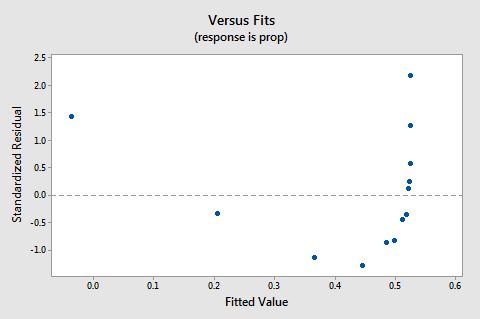
ponieważ brak liniowości dominuje na wykresie, nie możemy użyć wykresu do oceny, czy odchylenia błędu są równe. Musimy rozwiązać problem nieliniowości, zanim będziemy mogli ocenić założenie równych wariancji.
a co z normalnym wykresem prawdopodobieństwa pozostałości? Co sugeruje warunki błędu? Czy możemy stwierdzić, że są one normalnie dystrybuowane?
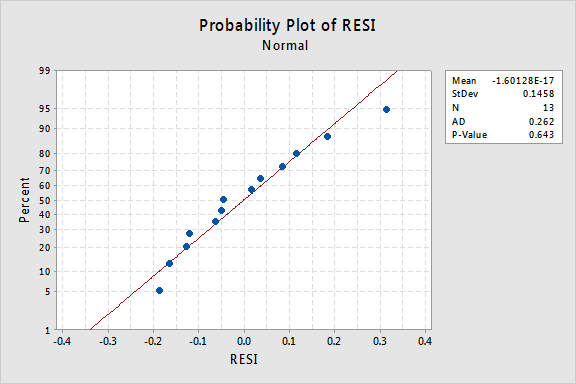
wartość P Andersona-Darlinga dla tego przykładu wynosi 0,643, co sugeruje, że nie odrzucamy hipotezy zerowej normalnych terminów błędów. Nie ma wystarczających dowodów, aby stwierdzić, że terminy błędów nie są normalne.
podsumowując, mamy zbiór danych, w którym Nieliniowość jest jedynym poważnym problemem. Taka sytuacja wymaga przekształcenia tylko wartości predyktora. Zanim to zrobimy, Weźmy na bok i omówmy „transformację logarytmiczną”, ponieważ jest to najczęstsza i najbardziej użyteczna transformacja danych dostępna.
transformacja logarytmiczna. Domyślna transformacja logarytmiczna polega jedynie na pobraniu logarytmu naturalnego-oznaczonego ln lub loge lub po prostu log-każdej wartości danych. Można rozważyć użycie innego rodzaju logarytmu, takiego jak logarytm o podstawie 10 lub logarytm o podstawie 2. Jednak logarytm naturalny – który można traktować jako logarytm o podstawie e, gdzie e jest stałą 2,718282… – jest najczęściej stosowaną skalą logarytmiczną stosowaną w pracach naukowych.
ogólna charakterystyka funkcji logarytmicznej naturalnej to:
- logarytm naturalny z x jest potęgą e = 2.718282… że musisz wziąć, aby otrzymać x. można to określić notacyjnie jako LN (ex) = x. na przykład logarytm naturalny z 5 jest potęgą, do której musisz podnieść e = 2.718282… aby uzyskać 5. Ponieważ 2,7182821,60944 wynosi w przybliżeniu 5, mówimy, że logarytm naturalny z 5 wynosi 1,60944. Notacyjnie mówimy ln (5) = 1,60944.
- logarytm naturalny z e jest równy 1, czyli ln(E) = 1.
- logarytm naturalny z jedynki jest równy zero, czyli ln(1) = 0.
wykres funkcji logarytmu naturalnego:
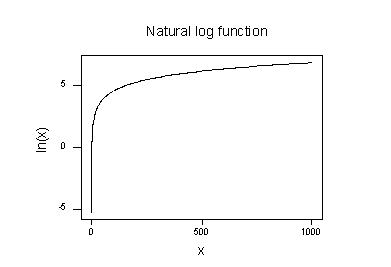
sugeruje, że efekty przekształcenia logarytmicznego naturalnego są następujące:
- małe wartości, które są blisko siebie, są dalej rozłożone.
- Duże wartości, które są rozłożone, są zbliżone do siebie.
powrót do przykładu. Użyjmy logarytmu naturalnego do przekształcenia wartości x w danych eksperymentu retencji pamięci. Ponieważ X = czas jest predyktorem, wszystko, co musimy zrobić, to wziąć logarytm naturalny każdej wartości czasu pojawiającej się w zbiorze danych. W ten sposób tworzymy nowo przekształcony predyktor o nazwie lntime:
| czas | prop | |
| 5 | 0.71 | 1.60944 |
| 15 | 0.61 | 2.70805 |
| 30 | 0.56 | 3.40120 |
| 60 | 0.54 | 4.09434 |
| 120 | 0.47 | 4.78749 |
| 240 | 0.45 | 5.48064 |
| 480 | 0.38 | 6.17379 |
| 720 | 0.36 | 6.57925 |
| 1440 | 0.26 | 7.27240 |
| 2880 | 0.20 | 7.96555 |
| 5760 | 0.16 | 8.65869 |
| 10080 | 0.08 | 9.21831 |
We take the natural logarithm for each value of time and place the results in their own column. Oznacza to, że „przekształcamy” każdą wartość czasu predyktora na wartość ln(czas). Na przykład, ln(1) = 0, ln(5) = 1,60944 i ln(15) = 2,70805 i tak dalej.
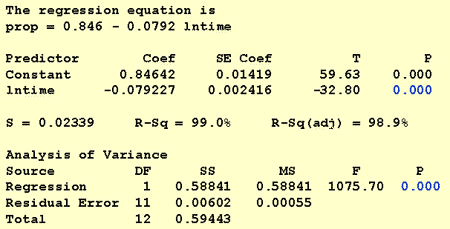
teraz, gdy przekształciliśmy wartości predyktora, zobaczmy, czy pomogło to skorygować nieliniowy trend w danych. Ponownie dopasowujemy model z y = prop jako odpowiedzią i X = lntime jako predyktorem.
uzyskany Wykres linii dopasowanej sugeruje, że pomocne jest wzięcie logarytmu naturalnego wartości predyktora.
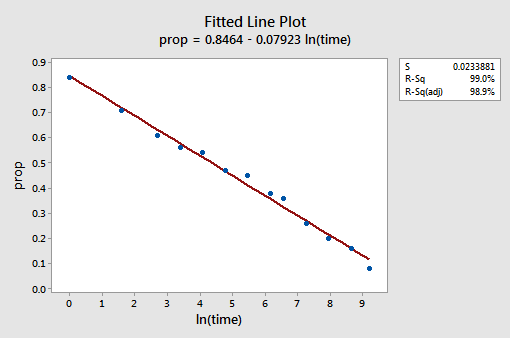
wartość R2 wzrosła z 57,1% do 99,0%. Mówi nam ona, że 99% zmienności proporcji przywołanych słów (prop) jest zmniejszane przez uwzględnienie naturalnego logarytmu czasu (lntime)!
nowy wykres rezydualny vs.fits wykazuje znaczną poprawę w stosunku do wykresu opartego na nieprzetransformowanych danych.
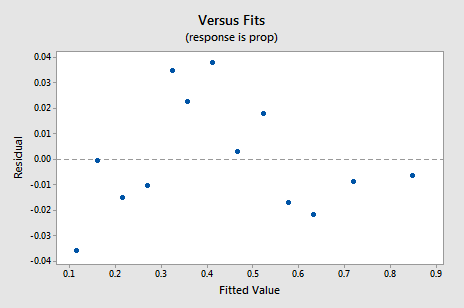
możesz się obawiać jakiegoś cyklicznego trendu w górę-w dół na wykresie. Ponownie ostrzegam, aby nie przesadzać z interpretacją tych wykresów, zwłaszcza gdy zestaw danych jest taki mały. Naprawdę nie powinieneś oczekiwać perfekcji, gdy uciekasz się do transformacji danych. Czasami trzeba po prostu zadowolić się znaczącymi ulepszeniami. Nawiasem mówiąc, Wykres sugeruje również, że można założyć, że odchylenia błędu są równe.
normalny Wykres prawdopodobieństwa pozostałości pokazuje, że przekształcenie wartości x nie miało wpływu na normalność terminów błędów:
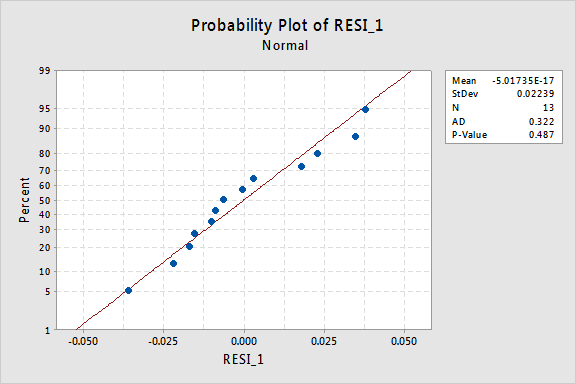
ponownie wartość P Andersona-Darlinga jest duża, więc nie odrzucamy hipotezy zerowej normalnych terminów błędów. Nie ma wystarczających dowodów, aby stwierdzić, że terminy błędów nie są normalne.
a gdybyśmy zamiast tego przekształcili wartości y? Wcześniej powiedziałem, że podczas gdy niektóre założenia mogą wydawać się trzymać przed zastosowaniem transformacji, mogą już nie trzymać się po zastosowaniu transformacji. Na przykład, jeśli terminy błędów są dobrze zachowywane, przekształcenie wartości y może zmienić je w źle zachowujące się terminy błędów. Terminy błędów dla danych przechowywanych w pamięci przed przekształceniem wartości x wydają się być dobrze zachowywane (w tym sensie, że wydają się w przybliżeniu normalne). Dlatego możemy się spodziewać, że przekształcenie wartości y zamiast wartości x może spowodować, że terminy błędów staną się źle zachowywane. Rzućmy okiem na dane dotyczące przechowywania pamięci, aby zobaczyć przykład tego, co może się zdarzyć, gdy przekształcimy wartości y, gdy Nieliniowość jest jedynym problemem.
metodą prób i błędów odkrywamy, że transformacja mocy y, która najlepiej koryguje Nieliniowość, to y-1,25. Dopasowany wykres liniowy ilustruje, że przekształcenie rzeczywiście wyprostowuje zależność-choć co prawda nie tak dobrze jak przekształcenie logarytmiczne wartości x.
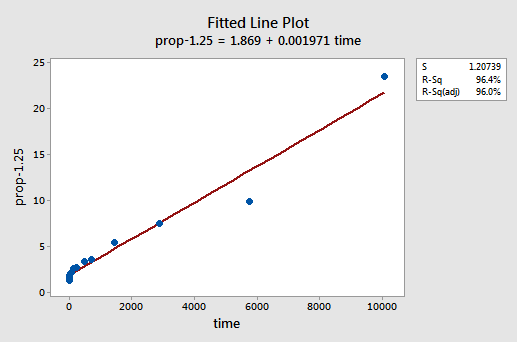
zauważ, że wartość R2 wzrosła z 57,1% do 96,4%.
pozostałości wykazują poprawę w odniesieniu do nieliniowości, chociaż poprawa nie jest wielka…
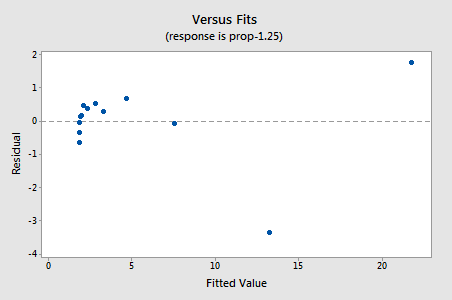
…ale teraz mamy nienormalne terminy błędów! Wartość P Andersona-Darlinga jest mniejsza niż 0,005, więc odrzucamy hipotezę zerową normalnych terminów błędów. Istnieją wystarczające dowody, aby stwierdzić, że terminy błędów nie są normalne:
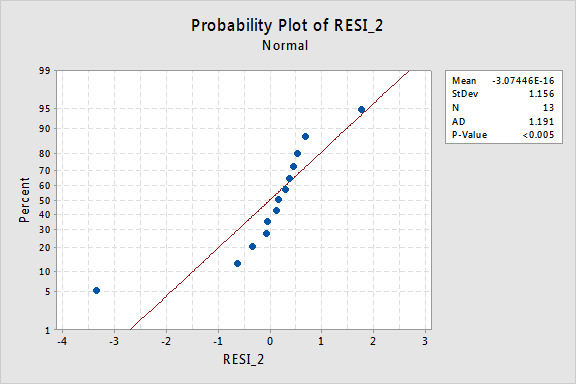
ponownie, jeśli terminy błędów są dobrze zachowywane przed transformacją, przekształcenie wartości y może zmienić je w źle zachowujące się terminy błędów.
Korzystanie z modelu
gdy już znajdziemy najlepszy model dla naszych danych regresji, możemy go użyć, aby odpowiedzieć na interesujące nas Pytania badawcze. Jeśli nasz model zawiera przekształcone wartości predyktora (x), możemy lub nie musimy wprowadzać drobnych modyfikacji do standardowych procedur, których już się nauczyliśmy.
użyjmy naszego modelu regresji liniowej dla danych retencji pamięci-z y = prop jako odpowiedzią i x = lntime jako predyktorem-aby odpowiedzieć na cztery różne pytania badawcze.
Pytanie badawcze # 1: Jaki jest charakter związku między czasem od zapamiętania a skutecznością przypomnienia?
aby odpowiedzieć na to pytanie badawcze, po prostu opisujemy naturę relacji. Oznacza to, że proporcja poprawnie zapamiętanych słów jest ujemnie liniowo związana z logiem naturalnym czasu, od którego słowa zostały zapamiętane. Nic dziwnego, że wraz ze wzrostem logarytmu naturalnego czasu zmniejsza się odsetek słów przywoływanych.
Pytanie badawcze #2: Czy istnieje związek między czasem od zapamiętania a skutecznością przypomnienia?
w odpowiedzi na to pytanie badawcze nie jest konieczna modyfikacja standardowej procedury. Po prostu testujemy hipotezę zerową H0: β1 = 0 używając testu F lub równoważnego testu t:
Jak pokazuje wyjście oprogramowania, wartość P wynosi < 0.001. Istnieją znaczące dowody na 0.05 poziom do wniosku, że istnieje Linearny związek między proporcją słów przywołanych i logarytmem naturalnym czasu od zapamiętania.
Pytanie badawcze #3: jakiej proporcji słów możemy oczekiwać, że losowo wybrana osoba przypomni sobie po 1000 minutach?
aby odpowiedzieć na to pytanie badawcze, musimy tylko obliczyć przedział Przewidywania — z jedną niewielką modyfikacją. Naszą zmienną predyktorową jest logarytm naturalny czasu. Dlatego, gdy używamy oprogramowania statystycznego do obliczania przedziału predykcji, musimy upewnić się, że określamy wartość wartości predyktora w jednostkach przekształconych, a nie w jednostkach pierwotnych. Logarytm naturalny z 1000 minut wynosi 6,91 log-minut. Korzystając z oprogramowania do obliczenia 95% przedziału predykcji, gdy lntime = 6.91, otrzymujemy:
wyjście mówi nam, że możemy być w 95% pewni, że po 1000 minut, losowo wybrana osoba przypomni sobie od 24,5% do 35.3% słów.
Pytanie badawcze #4: Jak bardzo zmienia się oczekiwane wycofanie, jeśli czas wzrasta dziesięciokrotnie?
jeśli się nad tym zastanowić, odpowiedź na to pytanie badawcze polega jedynie na oszacowaniu i interpretacji parametru nachylenia β1. Cóż, nie do końca – jest niewielka Regulacja. Ogólnie rzecz biorąc, K-krotne zwiększenie predyktora x jest związane z a:
β1 × LN(k)
zmiana średniej odpowiedzi y.
ta pochodna, która następuje, może pomóc ci zrozumieć i zapamiętać ten wzór.
oznacza to, że dziesięciokrotny wzrost x związany jest ze zmianą średniej y β1 × LN(10), a dwukrotny wzrost x związany jest ze zmianą średniej y β1 × ln(2).
ogólnie rzecz biorąc, należy używać tylko wielokrotności k, które mają sens dla zakresu modelu. Na przykład, jeśli wartości x w zestawie danych wahają się od 2 do 8, sensowne jest rozważenie tylko krotności K, które są 4 lub mniejsze. Gdyby wartość x wynosiła 2, dziesięciokrotny wzrost (tj. k = 10) wynosiłby od 2 do 2 × 10 = 20, wartości wykraczającej poza zakres modelu. W zestawie danych dotyczących retencji pamięci wartości predyktora wahają się od 1 do 10080, więc nie ma problemu z rozważeniem dziesięciokrotnego wzrostu.
Jeśli jesteśmy zainteresowani tylko otrzymaniem oszacowania punktowego, bierzemy jedynie oszacowanie parametru nachylenia (b1 = -0.079227) z wyjścia oprogramowania:

i mnożymy je przez ln(10):
B1 × LN(10) = -0.079227 × LN(10) = -0.182
spodziewamy się, że procent przywołanych słów zmniejszy się (ponieważ znak jest ujemny) 18.2% za każde dziesięciokrotne zwiększenie czasu od momentu zapamiętywania.
oczywiście ten punkt ma ograniczoną przydatność. Na ile możemy być pewni, że oszacowanie jest bliskie prawdziwej nieznanej wartości? Oczywiście, powinniśmy obliczyć 95% pewien przedział. Aby to zrobić, po prostu obliczamy 95% przedział ufności dla β1, jak zawsze: