nesta seção, aprendemos a construir e usar um modelo de regressão linear simples, transformando os valores do predictor X. Esta pode ser a primeira coisa que você tenta se você encontrar uma tendência não-linear em seus dados. Isto é, transformar os valores x é apropriado quando a não linearidade é o único problema (ou seja, a independência, normalidade e condições de variância iguais são cumpridas). Note, no entanto, que pode ser necessário corrigir a não linearidade antes que você possa avaliar a normalidade e iguais pressupostos de variância. Além disso, embora algumas suposições possam parecer válidas antes de aplicar uma transformação, elas não podem mais manter-se assim que uma transformação é aplicada. Em outras palavras, o uso de transformações é parte de um processo iterativo onde todas as suposições de regressão linear são re-verificadas após cada iteração.
tenha em mente que, embora estejamos focados num modelo de regressão linear simples aqui, as ideias essenciais aplicam-se mais geralmente a vários modelos de regressão linear também. Podemos considerar transformar qualquer um dos predictors examinando scatterplots dos residuals versus cada predictor por sua vez.
construir o modelo
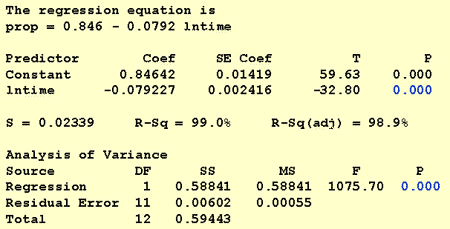
um exemplo. A maneira mais fácil de aprender sobre transformações de dados é por exemplo. Vamos considerar os dados de um experimento de retenção de memória em que 13 sujeitos foram convidados a memorizar uma lista de itens desconectados. Os sujeitos foram então convidados a recordar os itens em várias vezes até uma semana mais tarde. A proporção de itens (y = prop) corretamente relembrados em várias vezes (x = Tempo, em minutos) desde que a lista foi memorizada foram registrados (wordrecall.= = ligações externas = = Reconhecendo que não há uma boa razão para que os Termos de erro não sejam independentes, vamos avaliar as três condições restantes — linearidade, normalidade e variâncias iguais — do modelo.a parcela de linha ajustada resultante sugere que a proporção de itens recolhidos (y) não está linearmente relacionada com o tempo (x):
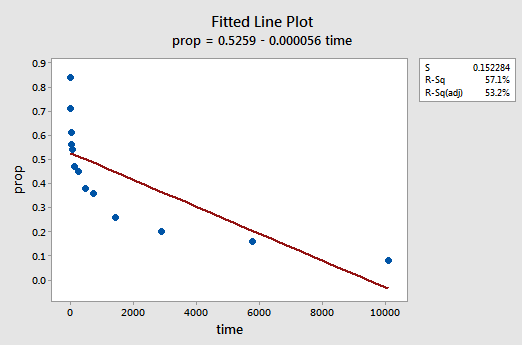
O gráfico resíduos vs. ajustes também sugere que a relação não é linear:
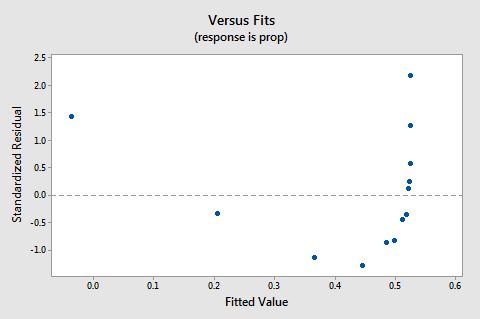
Devido a falta de linearidade domina o enredo, não podemos usar o enredo para avaliar se é ou não o erro variâncias são iguais. Temos de resolver o problema da não linearidade antes de podermos avaliar a hipótese de variações iguais.e o gráfico de probabilidade normal dos resíduos? O que sugere sobre os Termos de erro? Podemos concluir que são normalmente distribuídas?
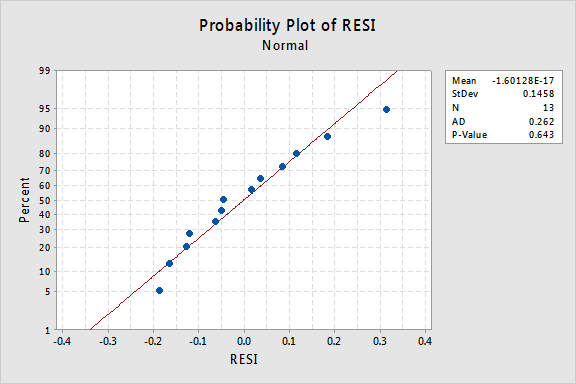
o valor de P Anderson-Darling para este exemplo é 0.643, o que sugere que não rejeitamos a hipótese nula de termos de erro normais. Não existem provas suficientes para concluir que os termos dos erros não são normais.
em resumo, temos um conjunto de dados em que a não linearidade é o único grande problema. Esta situação grita para transformar apenas os valores do predictor. Antes de fazermos isso, vamos deixar de lado e discutir a “transformação logarítmica”, uma vez que é a transformação de dados mais comum e mais útil disponível.
a transformação logarítmica. A transformação logarítmica padrão envolve simplesmente tomar o logaritmo natural-denotado ln ou loge ou simplesmente log — de cada valor de dados. Pode-se considerar tomar um tipo diferente de logaritmo, como log base 10 ou log base 2. No entanto, o logaritmo natural — que pode ser pensado como log base e onde e é a constante 2.718282… — é a escala logarítmica mais comum utilizada no trabalho científico.
As características gerais da função logarítmica natural são:
- o logaritmo natural de x é a potência de e = 2.718282… isso você tem que tomar a fim de obter X. Isso pode ser indicado notacionalmente como ln(ex) = X. por exemplo, o logaritmo natural de 5 é o poder para o qual você tem que elevar e = 2.718282. .. para conseguir 5. Desde 2,7182821.60944 é aproximadamente 5, dizemos que o logaritmo natural de 5 é 1,60944. Notacionalmente, dizemos ln ( 5) = 1.60944.o logaritmo natural de e é igual a um, ou seja, ln(E) = 1.
- o logaritmo natural de um é igual a zero, ou seja, ln(1) = 0.
O gráfico do logaritmo natural da função:
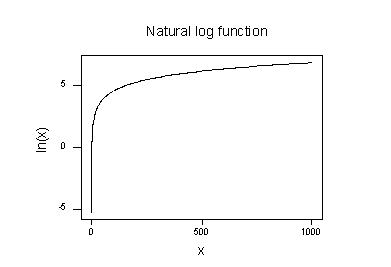
sugere que os efeitos de tomar a natural transformação logarítmica são:
- valores Pequenos que estão juntos são distribuídos mais adiante.os grandes valores que se distribuem estão mais próximos.
de volta ao exemplo. Vamos usar o logaritmo natural para transformar os valores x nos dados do experimento de retenção de memória. Uma vez que x = tempo é o predictor, tudo o que precisamos fazer é tomar o logaritmo natural de cada valor de tempo que aparece no conjunto de dados. Ao fazer isso, criamos um recém-transformada preditor chamado lntime:
| tempo | prop | lntime |
| 1 | 0.84 | 0.00000 |
| 5 | 0.71 | 1.60944 |
| 15 | 0.61 | 2.70805 |
| 30 | 0.56 | 3.40120 |
| 60 | 0.54 | 4.09434 |
| 120 | 0.47 | 4.78749 |
| 240 | 0.45 | 5.48064 |
| 480 | 0.38 | 6.17379 |
| 720 | 0.36 | 6.57925 |
| 1440 | 0.26 | 7.27240 |
| 2880 | 0.20 | 7.96555 |
| 5760 | 0.16 | 8.65869 |
| 10080 | 0.08 | 9.21831 |
We take the natural logarithm for each value of time and place the results in their own column. Isto é, nós” transformamos ” cada valor de tempo de predictor para um valor ln(tempo). Por exemplo, ln(1) = 0, ln(5) = 1.60944, e ln(15) = 2.70805, e assim por diante.
Agora que transformamos os valores de predictor, vamos ver se ajudou a corrigir a tendência não-linear nos dados. Nós re-encaixamos o modelo com y = prop como a resposta e x = intime como o predictor.
a parcela de linha ajustada resultante sugere que tomar o logaritmo natural dos valores do predictor é útil.
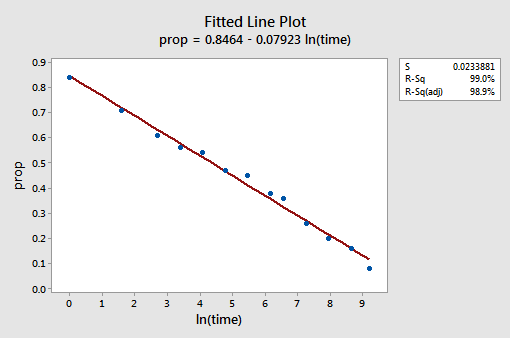
de facto, o valor R2 aumentou de 57,1% para 99,0%. Diz – nos que 99% da variação na proporção de palavras lembradas (prop) é reduzida tendo em conta o log natural do tempo (lntime)!a nova parcela residual vs. fits mostra uma melhoria significativa em relação à baseada nos dados não traduzidos.
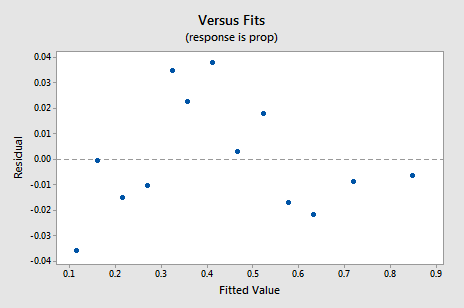
Pode preocupar-se com algum tipo de tendência cíclica ascendente na parcela. Aviso-o mais uma vez para não interpretar demasiado estas parcelas, especialmente quando o conjunto de dados é pequeno como este. Você realmente não deve esperar perfeição quando você recorre a tomar transformações de dados. Por vezes, temos de nos contentar com melhorias significativas. A propósito, o enredo também sugere que não faz mal assumir que as variações de erro são iguais.
a parcela de probabilidade normal dos resíduos mostra que a transformação dos valores de x não teve qualquer efeito na normalidade dos Termos de erro:
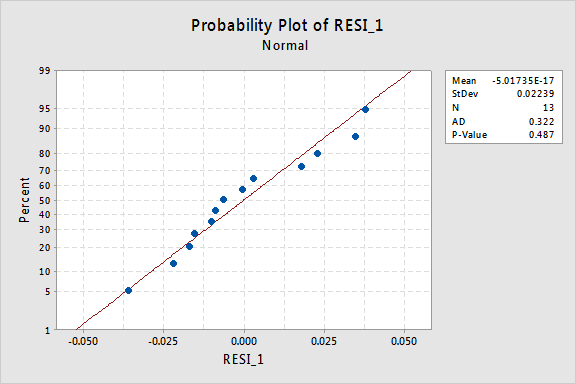
Mais uma vez o valor de P Anderson-Darling é grande, por isso não conseguimos rejeitar a hipótese nula dos Termos de erro normais. Não existem provas suficientes para concluir que os termos dos erros não são normais.e se tivéssemos transformado os valores em y? Anteriormente eu disse que enquanto algumas suposições podem parecer manter Antes de aplicar uma transformação, eles podem não mais manter uma vez que uma transformação é aplicada. Por exemplo, se os Termos de erro forem bem comportados, transformar os valores de y poderia transformá-los em termos de erro mal comportados. Os Termos de erro para os dados de retenção de memória antes de transformar os valores x parecem ser bem comportados (no sentido de que eles parecem aproximadamente normais). Portanto, podemos esperar que transformar os valores y em vez dos valores x possa fazer com que os Termos de erro se tornem mal comportados. Vamos dar uma olhada rápida nos dados de retenção de memória para ver um exemplo do que pode acontecer quando transformamos os valores de y quando a não linearidade é o único problema.
por tentativa e erro, descobrimos que a transformação de poder de y que faz o melhor trabalho para corrigir a não linearidade é y-1,25. A parcela de linha ajustada ilustra que a transformação realmente endireita a relação — embora reconhecidamente não, bem como a transformação logarítmica dos valores x.
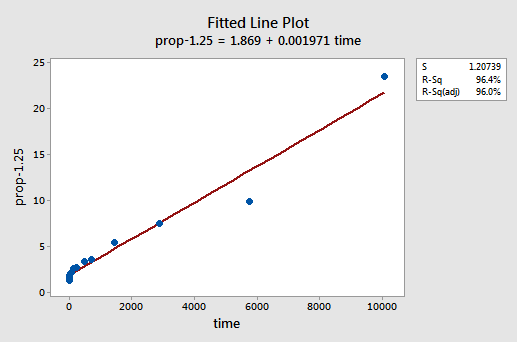
Note que o valor R2 aumentou de 57.1% para 96.4%.os resíduos mostram uma melhoria em relação à não linearidade, embora a melhoria não seja grande…
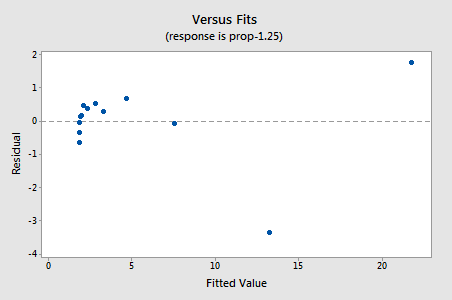
…mas agora temos Termos de erro Não-normais! O valor de P de Anderson Darling é inferior a 0,005, por isso rejeitamos a hipótese nula dos Termos de erro normais. Existem provas suficientes para concluir que os Termos de erro não são normais:
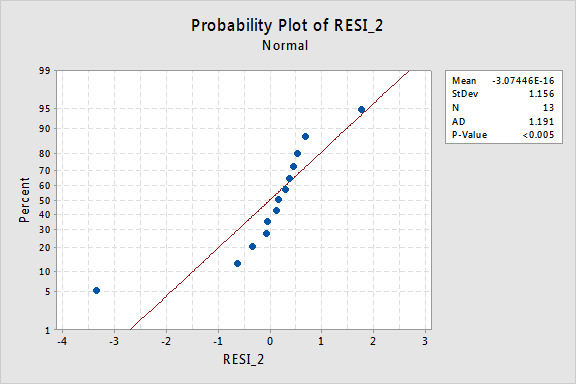
novamente, se os Termos de erro forem bem comportados antes da transformação, a transformação dos valores em y pode alterá-los em termos de erro mal comportados.
usando o modelo
Uma vez que tenhamos encontrado o melhor modelo para os nossos dados de regressão, podemos então usar o modelo para responder às nossas questões de investigação de interesse. Se nosso modelo envolve valores de predictor transformado (x), podemos ou não ter que fazer pequenas modificações nos procedimentos padrão que já aprendemos.
vamos usar o nosso modelo de regressão linear para os dados de retenção de memória—com y = prop como Resposta e x = tempo como predictor—para responder a quatro perguntas de pesquisa diferentes.pergunta de Investigação # 1: Qual é a natureza da associação entre o tempo memorizado e a eficácia da recolha?
Para responder a esta questão de investigação, acabamos de descrever a natureza da relação. Ou seja, a proporção de palavras corretamente lembradas é negativamente linearmente relacionada com o log natural do tempo desde que as palavras foram memorizadas. Não surpreendentemente, à medida que o log do tempo natural aumenta, a proporção de palavras lembradas diminui.pergunta de pesquisa #2: Existe uma associação entre o tempo desde memorizado e a eficácia do recall?ao responder a esta pergunta de investigação, não é necessário alterar o procedimento padrão. Nós simplesmente testar a hipótese nula H0: β1 = 0 utilizando-se o teste F, ou o equivalente teste-t:
Como a produção de software ilustra, o P-valor é < 0.001. Há provas significativas no 0.05 nível para concluir que há uma associação linear entre a proporção de palavras lembradas e o log natural do tempo desde memorizado.pergunta de pesquisa #3: que proporção de palavras podemos esperar que uma pessoa selecionada aleatoriamente recorde após 1000 minutos?
apenas precisamos calcular um intervalo de previsão-com uma ligeira modificação-para responder a esta pergunta de pesquisa. Nossa variável predictor é o log natural do tempo. Portanto, quando usamos software estatístico para calcular o intervalo de previsão, temos que nos certificar de que especificamos o valor dos valores de predictor nas unidades transformadas, não as unidades originais. O log natural de 1000 minutos é de 6,91 log-minutos. Usando o software para calcular 95% de intervalo de predição quando lntime = 6.91, obtém-se:
A saída nos diz que podemos ser de 95% de confiança que, após 1000 minutos, aleatoriamente seleccionada pessoa vai lembrar de entre 24,5% e 35.3% das palavras.pergunta de pesquisa #4: quanto é que a recolha esperada muda se o tempo aumentar dez vezes?se você pensar sobre isso, responder a esta pergunta de pesquisa apenas envolve estimar e interpretar o parâmetro de declive β1. Bem, não exactamente … há um pequeno ajuste. Em geral, um k-fold aumento do preditor x está associado a:
β1 × ln(k)
mudança na média da resposta y.
Esta derivação que se segue pode ajudar a compreender e, portanto, lembre-se desta fórmula.
isto é, um aumento de dez vezes no x está associado a um β1 × ln(10) mudança na média de y. E, um aumento de duas vezes x é associado a um β1 × ln(2) mudança na média de y.
Em geral, você só deve usar múltiplos de k que fazem sentido para o escopo do modelo. Por exemplo, se os valores x no seu conjunto de dados variam de 2 a 8, faz sentido considerar múltiplos k que são 4 ou menores. Se o valor de x fosse 2, um aumento de dez vezes (ou seja, k = 10) levá-lo-ia de 2 até 2 × 10 = 20, um valor fora do escopo do modelo. No conjunto de dados de retenção de memória, os valores de predictor variam de 1 a 10080, então não há problema em considerar um aumento de dez vezes.
Se estamos interessados apenas na obtenção de uma estimativa pontual, nós simplesmente tomar a estimativa do parâmetro de inclinação (b1 = -0.079227) a partir do software de saída:

e multiplicá-lo por ln(10):
b1 × ln(10) = -0.079227 × ln(10) = -0.182
esperamos que o percentual de recordou palavras para diminuir (desde que o sinal é negativo) 18.2% para cada aumento de dez vezes no tempo desde que a memorização ocorreu.
naturalmente, esta estimativa pontual é de utilidade limitada. Quão confiantes podemos estar de que a estimativa está perto do verdadeiro valor desconhecido? Naturalmente, devemos calcular um intervalo de confiança de 95%. Para isso, basta calcular um intervalo de confiança de 95% para β1 como sempre temos: