i det här avsnittet lär vi oss att bygga och använda en enkel linjär regressionsmodell genom att omvandla prediktor X-värdena. Det här kan vara det första du försöker om du hittar en icke-linjär trend i dina data. Det vill säga att omvandla x-värdena är lämpligt när icke-linjäritet är det enda problemet (dvs oberoende, normalitet och lika variansvillkor är uppfyllda). Observera dock att det kan vara nödvändigt att korrigera icke-linjäritet innan du kan bedöma normalitet och lika varians antaganden. Även om vissa antaganden kan tyckas hålla innan en omvandling tillämpas, kan de inte längre hålla när en omvandling tillämpas. Med andra ord är användning av transformationer en del av en iterativ process där alla linjära regressionsantaganden kontrolleras igen efter varje iteration.
Tänk på att även om vi fokuserar på en enkel linjär regressionsmodell här, gäller de väsentliga ideerna mer generellt för flera linjära regressionsmodeller också. Vi kan överväga att omvandla någon av prediktorerna genom att undersöka scatterplots av resterna kontra varje prediktor i sin tur.
bygga modellen
ett exempel. Det enklaste sättet att lära sig om datatransformationer är genom exempel. Låt oss överväga data från ett minnesretentionsexperiment där 13 personer ombads att memorera en lista med frånkopplade objekt. Ämnena ombads sedan att återkalla föremålen vid olika tidpunkter upp till en vecka senare. Andelen objekt (y = prop) korrekt återkallad vid olika tidpunkter (x = Tid, i minuter) sedan listan memorerades registrerades (wordrecall.txt) och plottas. Att erkänna att det inte finns någon bra anledning att felvillkoren inte skulle vara oberoende, låt oss utvärdera de återstående tre villkoren — linjäritet, normalitet och lika variationer — av modellen.
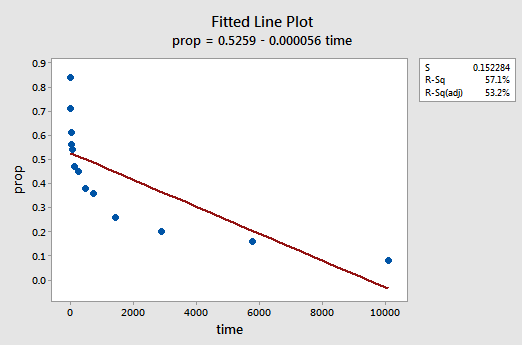
den resulterande anpassade linjediagrammet antyder att andelen återkallade objekt (y) inte är linjärt relaterad till tiden (x):
resterna vs. passar plot föreslår också att förhållandet inte är linjärt:
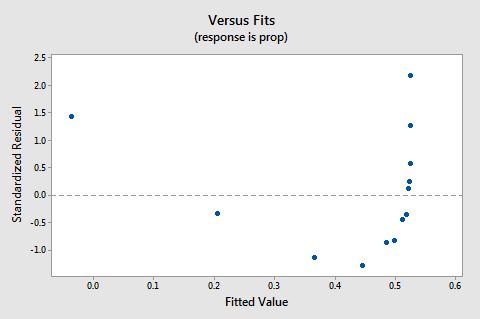
eftersom bristen på linjäritet dominerar tomten kan vi inte använda tomten för att utvärdera huruvida felvariationerna är lika eller inte. Vi måste åtgärda icke-linjäritetsproblemet innan vi kan bedöma antagandet om lika avvikelser.
vad sägs om den normala sannolikhetsdiagrammet för resterna? Vad föreslår det om felvillkoren? Kan vi dra slutsatsen att de normalt distribueras?
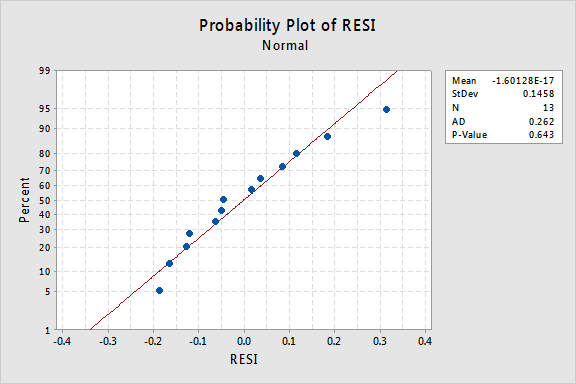
Anderson-Darling P-värdet för detta exempel är 0.643, vilket tyder på att vi inte avvisar nollhypotesen för normala feltermer. Det finns inte tillräckligt med bevis för att dra slutsatsen att felvillkoren inte är normala.
Sammanfattningsvis har vi en datamängd där icke-linjäritet är det enda stora problemet. Denna situation skriker ut för att bara omvandla prediktorns värden. Innan vi gör det, låt oss ta en sida och diskutera den ”logaritmiska omvandlingen”, eftersom det är den vanligaste och mest användbara datatransformationen som finns tillgänglig.
den logaritmiska omvandlingen. Standard logaritmisk transformation innebär bara att ta den naturliga logaritmen-betecknad ln eller loge eller helt enkelt logga — för varje datavärde. Man kan överväga att ta en annan typ av logaritm, såsom log base 10 eller log base 2. Men den naturliga logaritmen – som kan betraktas som loggbas e där e är konstanten 2.718282… – är den vanligaste logaritmiska skalan som används i vetenskapligt arbete.
de allmänna egenskaperna hos den naturliga logaritmfunktionen är:
- den naturliga logaritmen för x är effekten av e = 2.718282… att du måste ta för att få x. detta kan anges notationally som ln(ex) = x.till exempel är den naturliga logaritmen av 5 den kraft som du måste höja e = 2.718282… för att få 5. Eftersom 2.7182821.60944 är ungefär 5, säger vi att den naturliga logaritmen för 5 är 1.60944. Notationally säger Vi ln (5) = 1.60944.
- den naturliga logaritmen för e är lika med en, det vill säga ln(e) = 1.
- den naturliga logaritmen för en är lika med noll, det vill säga ln(1) = 0.
plot av den naturliga logaritmfunktionen:
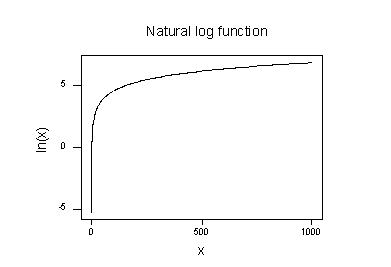
föreslår att effekterna av att ta den naturliga logaritmiska omvandlingen är:
- små värden som ligger nära varandra sprids längre ut.
- stora värden som sprids ut förs närmare varandra.
tillbaka till exemplet. Låt oss använda den naturliga logaritmen för att omvandla X-värdena i minnesretentionsexperimentdata. Eftersom x = tid är prediktorn är allt vi behöver göra att ta den naturliga logaritmen för varje tidsvärde som visas i datamängden. På så sätt skapar vi en nyligen transformerad prediktor som heter lntime:
| tid | prop | lntime |
| 1 | 0.84 | 0.00000 |
| 5 | 0.71 | 1.60944 |
| 15 | 0.61 | 2.70805 |
| 30 | 0.56 | 3.40120 |
| 60 | 0.54 | 4.09434 |
| 120 | 0.47 | 4.78749 |
| 240 | 0.45 | 5.48064 |
| 480 | 0.38 | 6.17379 |
| 720 | 0.36 | 6.57925 |
| 1440 | 0.26 | 7.27240 |
| 2880 | 0.20 | 7.96555 |
| 5760 | 0.16 | 8.65869 |
| 10080 | 0.08 | 9.21831 |
We take the natural logarithm for each value of time and place the results in their own column. Det vill säga, vi” omvandlar ” varje prediktortidsvärde till ett ln-värde(tid). Till exempel ln(1) = 0, ln(5) = 1.60944 och ln(15) = 2.70805, och så vidare.
Nu när vi har transformerat prediktorvärdena, låt oss se om det hjälpte till att korrigera den icke-linjära trenden i data. Vi anpassar modellen igen med y = prop som svar och x = lntime som prediktor.
den resulterande anpassade linjediagrammet antyder att det är användbart att ta den naturliga logaritmen för prediktorvärdena.
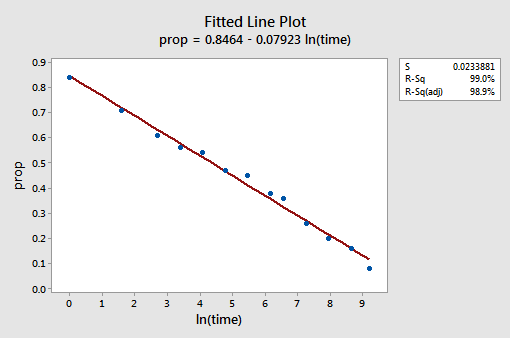
R2-värdet har faktiskt ökat från 57,1% till 99,0%. Det berättar för oss att 99% av variationen i andelen återkallade ord (prop) reduceras genom att ta hänsyn till den naturliga tidsloggen (lntime)!
den nya Rest vs. fits-diagrammet visar en signifikant förbättring jämfört med den som baseras på de omformade data.
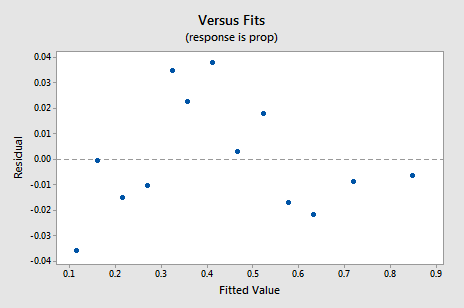
Du kan bli orolig för någon form av en upp-ner cyklisk trend i diagrammet. Jag varnar dig igen för att inte övertolka dessa tomter, särskilt när datamängden är liten så här. Du borde verkligen inte förvänta dig perfektion när du tillgriper datatransformationer. Ibland måste du bara vara nöjd med betydande förbättringar. Förresten föreslår plottet också att det är okej att anta att felvariationerna är lika.
den normala sannolikhetsdiagrammet för resterna visar att omvandling av x-värdena inte hade någon effekt på feltermens normalitet:
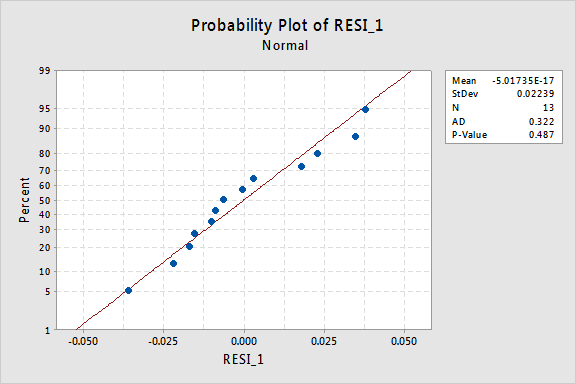
återigen är Anderson-Darling P-värdet stort, så vi misslyckas med att avvisa nollhypotesen för normala feltermer. Det finns inte tillräckligt med bevis för att dra slutsatsen att felvillkoren inte är normala.
vad händer om vi hade förändrat Y-värdena istället? Tidigare sa jag att medan vissa antaganden kan tyckas hålla innan de tillämpar en omvandling, kan de inte längre hålla när en omvandling tillämpas. Till exempel, om feltermerna är väluppfostrade, kan omvandling av Y-värdena ändra dem till dåligt uppförda feltermer. Felvillkoren för minneslagringsdata före omvandling av X-värdena verkar vara väluppfostrade (i den meningen att de verkar ungefär normala). Därför kan vi förvänta oss att omvandling av y-värdena istället för x-värdena kan leda till att felvillkoren blir dåligt uppförda. Låt oss ta en snabb titt på minneslagringsdata för att se ett exempel på vad som kan hända när vi omvandlar Y-värdena när icke-linjäritet är det enda problemet.
genom försök och fel upptäcker vi att kraftomvandlingen av y som gör det bästa jobbet för att korrigera icke-linjäriteten är y-1.25. Den monterade linjediagrammet illustrerar att omvandlingen verkligen rätar ut förhållandet — även om det visserligen inte är lika bra som loggtransformationen av x-värdena.
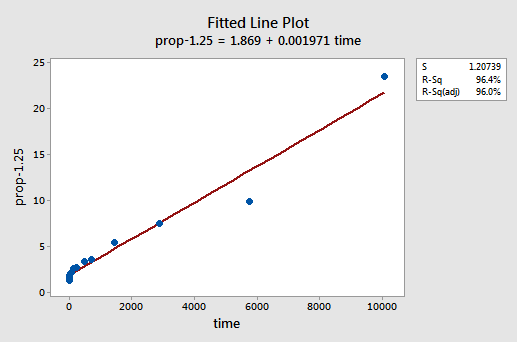
Observera att R2-värdet har ökat från 57,1% till 96,4%.
resterna visar en förbättring med avseende på icke-linjäritet, även om förbättringen inte är stor…
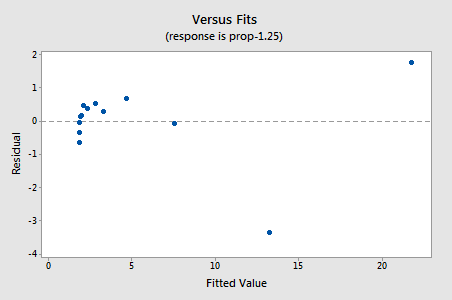
…men nu har vi icke-normala felvillkor! Anderson-Darling P-värdet är mindre än 0,005, så vi avvisar nollhypotesen för normala feltermer. Det finns tillräckliga bevis för att dra slutsatsen att feltermerna inte är normala:
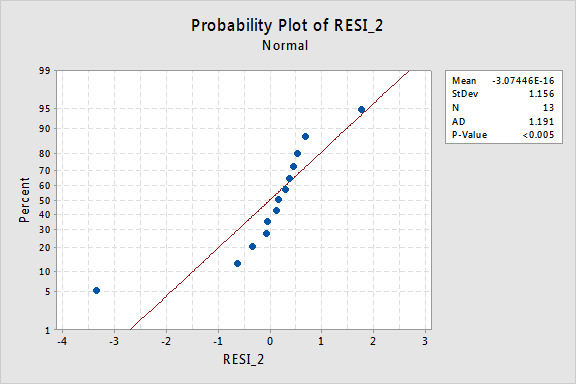
återigen, om feltermerna är väluppfostrade före omvandling kan omvandling av y-värdena ändra dem till dåligt uppförda feltermer.
använda modellen
När vi har hittat den bästa modellen för våra regressionsdata kan vi sedan använda modellen för att svara på våra forskningsfrågor av intresse. Om vår modell involverar transformerade prediktorvärden (x) kan vi eller kanske inte behöva göra små ändringar av de standardprocedurer vi redan har lärt oss.
Låt oss använda vår linjära regressionsmodell för minnesretentionsdata—med y = prop som svar och x = lntime som prediktor—för att svara på fyra olika forskningsfrågor.
forskningsfråga # 1: Vad är arten av sambandet mellan tiden sedan memorerad och effektiviteten av återkallelse?
för att svara på denna forskningsfråga beskriver vi bara förhållandet. Det vill säga andelen korrekt återkallade ord är negativt linjärt relaterad till den naturliga loggen för tiden sedan orden memorerades. Inte överraskande, när den naturliga tidsloggen ökar, minskar andelen återkallade ord.
forskningsfråga # 2: finns det en koppling mellan tid sedan memorerad och effektivitet av återkallelse?
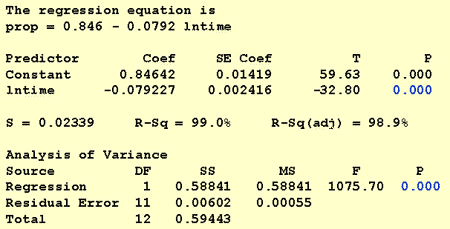
för att svara på denna forskningsfråga är ingen ändring av standardproceduren nödvändig. Vi testar bara nollhypotesen H0: 2B = 0 med antingen F-testet eller motsvarande t-test:
som programvaruutgången illustrerar är P-värdet < 0.001. Det finns betydande bevis på 0.05 nivå för att dra slutsatsen att det finns en linjär koppling mellan andelen ord som återkallas och den naturliga loggen för tiden sedan memorerade.
forskningsfråga # 3: vilken andel ord kan vi förvänta oss att en slumpmässigt vald person kommer ihåg efter 1000 minuter?
Vi behöver bara beräkna ett prediktionsintervall — med en liten modifiering-för att svara på denna forskningsfråga. Vår prediktorvariabel är den naturliga tidsloggen. Därför, när vi använder statistisk programvara för att beräkna prediktionsintervallet, måste vi se till att vi anger värdet på prediktorvärdena i de transformerade enheterna, inte de ursprungliga enheterna. Den naturliga loggen på 1000 minuter är 6,91 loggminuter. Med hjälp av programvara för att beräkna ett 95% prediktionsintervall när lntime = 6.91 erhåller vi:
utmatningen berättar för oss att vi kan vara 95% säkra på att, efter det att vi har 1000 minuter kommer en slumpmässigt vald person att återkalla mellan 24,5% och 35.3% av orden.
forskningsfråga # 4: Hur mycket ändras den förväntade återkallelsen om tiden ökar tio gånger?
om du tänker på det, att svara på denna forskningsfråga innebär bara att uppskatta och tolka lutningsparametern jacob1. Tja, inte riktigt—det finns en liten justering. I allmänhet är en k-faldig ökning av prediktorn x associerad med a:
2C1 1CB ln(k)
förändring i medelvärdet av svaret y.
denna härledning som följer kan hjälpa dig att förstå och därför komma ihåg denna formel.
det vill säga en tiofaldig ökning av x är förknippad med en ändring i medelvärdet av Y i 1 10-talet av 10-talet. och en tvåfaldig ökning av x är förknippad med en ändring i medelvärdet av Y i 1 1-talet av 2-talet av 1-talet av x.
i allmänhet bör du bara använda multiplar av k som är vettiga för modellens omfattning. Till exempel, om X-värdena i din datamängd sträcker sig från 2 till 8, är det bara meningsfullt att överväga k-multiplar som är 4 eller mindre. Om värdet på x var 2, skulle en tiofaldig ökning (dvs. k = 10) ta dig från 2 upp till 2 kcal 10 = 20, ett värde utanför modellens omfattning. I minneslagringsdatauppsättningen varierar prediktorvärdena från 1 till 10080, så det finns inga problem med att överväga en tiofaldig ökning.
Om vi bara är intresserade av att få en punktuppskattning tar vi bara uppskattningen av lutningsparametern (b1 = -0.079227) från programvaruutgången:

och multiplicerar den med ln(10):
B1 oc ln(10) = -0.079227 oc ln(10) = -0.182
vi förväntar oss att andelen återkallade ord minskar (eftersom tecknet är negativt) 18.2% för varje tiofaldig ökning av tiden sedan memorering ägde rum.
naturligtvis är denna punktuppskattning av begränsad användbarhet. Hur säker kan vi vara på att uppskattningen ligger nära det sanna okända värdet? Naturligtvis bör vi beräkna ett 95% säkert intervall. För att göra det, beräknar vi bara ett 95% konfidensintervall för XX1 som vi alltid har: