När en obligation säljs med rabatt måste obligationsrabatten skrivas av till räntekostnader under obligationens löptid. Eftersom debiteringsbeloppet i Kontorabatten på obligationer som ska betalas kommer att flyttas till kontoens räntekostnad, kommer avskrivningen att leda till att varje periods räntekostnad blir större än det räntebelopp som betalats under vart och ett av de år som obligationen är utestående.
den föredragna metoden för avskrivning av obligationsrabatten är effektivräntemetoden eller effektivräntemetoden. Enligt effektivräntemetoden kommer räntekostnadsbeloppet under en viss räkenskapsperiod att korrelera med beloppet för en obligations bokförda värde i början av räkenskapsperioden. Detta innebär att när en obligations bokförda värde ökar kommer räntekostnaden att öka.
innan vi visar den effektiva räntemetoden för en 5-årig 9% $100,000-obligation utfärdad på en 10% – marknad för $96,149, låt oss lyfta fram några punkter:
-
obligationsrabatten på $3,851 måste skrivas av till räntekostnader under obligationens livstid. Avskrivningen kommer att leda till att obligationens bokförda värde ökar från $ 96,149 den 1 januari 2019 till $100,000 strax före obligationen förfaller den 31 December 2023.
-
företaget måste göra en räntebetalning på $4,500 ($100,000 x 9% x 6/12) på varje Juni 30 och December 31 att obligationerna är utestående. Kontantkontot kommer att krediteras för $4,500 på vart och ett av dessa datum.
-
den effektiva räntan är marknadsräntan den dag då obligationerna emitterades. I vårt exempel var marknadsräntan den 1 januari 2019 5% per halvårsperiod under 10 halvårsperioder.
-
den effektiva räntan multipliceras gånger obligationens bokförda värde i början av räkenskapsperioden för att komma fram till varje periods räntekostnad.
-
skillnaden mellan punkt 2 och punkt 4 är avskrivningsbeloppet.
Följande tabell illustrerar den effektiva räntemetoden för att amortera rabatten på $3,851 på obligationer som ska betalas:
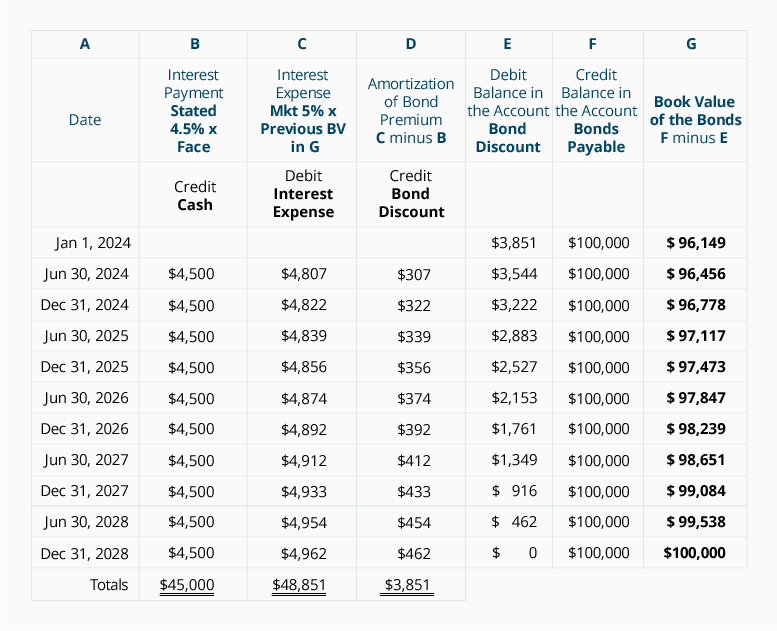
låt oss göra några punkter om ovanstående tabell:
-
kolumn B visar de räntebetalningar som krävs av obligationsavtalet: obligationens angivna ränta på 9% per år dividerat med två halvårsperioder = 4,5% per halvårsperiod multiplicerat gånger obligationens nominella belopp.
-
kolumn C visar räntekostnaden. Denna beräkning använder marknadsräntan vid den tidpunkt då obligationerna emitterades: Marknadsräntan på 10% per år dividerat med två halvårsperioder = 5% halvårsvis.
-
räntekostnaden i kolumn C är produkten av marknadsräntan på 5% per halvårsperiod gånger obligationens bokförda värde vid halvårsperiodens början. Lägg märke till hur räntekostnaden ökar med ökningen av bokfört värde i kolumn G. denna korrelation mellan räntekostnaden och obligationens bokförda värde gör effektivräntemetoden till den föredragna metoden för att amortera rabatten på obligationer som ska betalas.
-
eftersom de nuvärdesfaktorer som vi använde avrundades till tre decimalpositioner är våra beräkningar inte lika exakta som de belopp som bestämdes med hjälp av datorprogramvara, en finansiell kalkylator eller faktorer som utfördes till fler decimaler. Som ett resultat krävde vårt amorteringsbelopp 2023 en liten justering.
om bolaget endast utfärdar årsredovisningar och räkenskapsåret löper ut den 31 December kan avskrivningen av obligationsrabatten bokföras på räntebetalningsdagen med hjälp av beloppen från schemat ovan. I vårt exempel finns det ingen upplupen ränta vid emissionsdagen för obligationerna och i slutet av varje räkenskapsår eftersom obligationerna betalar ränta den 30 juni och 31 December. Posterna för 2019, inklusive posten för att registrera obligationsemissionen, visas nästa.
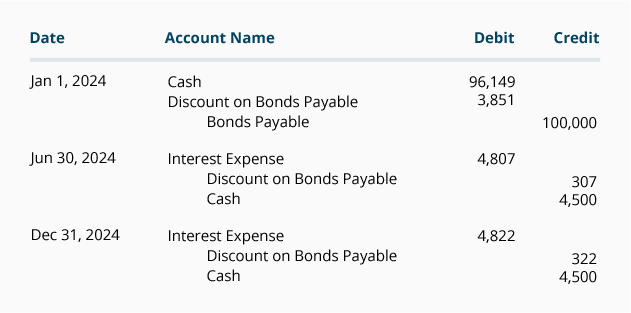
journalanteckningarna för år 2020 är:

journalanteckningarna för åren 2021 till 2023 kommer också att tas från schemat som visas ovan.
jämförelse av Amorteringsmetoder
nedan är en jämförelse av räntekostnaden som redovisas enligt effektivräntemetoden och linjärmetoden. Observera att enligt effektivräntemetoden ökar räntekostnaden för varje år i takt med att obligationens bokförda värde ökar. Enligt linjärmetoden förblir räntekostnaden konstant trots att obligationens bokförda värde ökar. Bokföringsyrket föredrar den effektiva räntemetoden, men tillåter den raka metoden när mängden obligationsrabatt inte är signifikant.
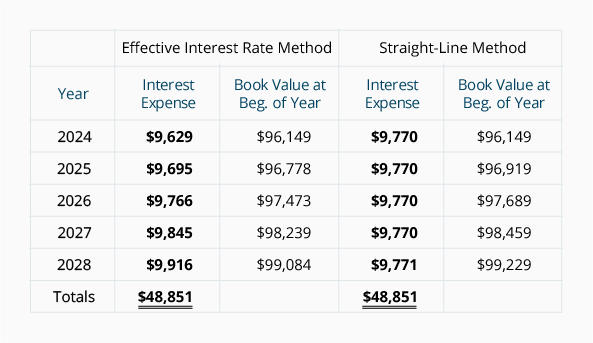
Observera att under båda amorteringsmetoderna rör sig det bokförda värdet vid den tidpunkt då obligationerna utfärdades ($96,149) mot obligationens löptidsvärde på $100,000. Anledningen är att obligationsrabatten på $3,851 reduceras till $0 eftersom obligationsrabatten skrivs av till räntekostnader.
märker också att under båda metoderna är den totala räntekostnaden under obligationernas livslängd $48,851 ($45,000 av räntebetalningar plus $3,851 av obligationsrabatten.)
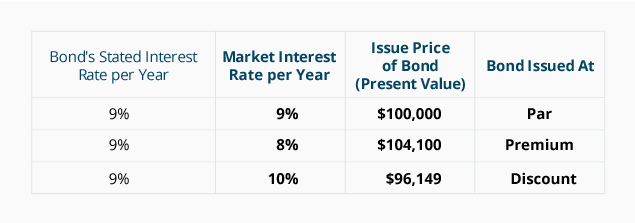
sammanfattning av effekten av marknadsräntor på en obligations emissionskurs
Följande tabell sammanfattar effekten av förändringen i marknadsräntan på en befintlig $100,000 obligation med en angiven ränta på 9% och förfaller i 5 år.