tässä osiossa opimme rakentamaan ja käyttämään yksinkertaista lineaarista regressiomallia muuntamalla predikaattori x-arvot. Tämä voi olla ensimmäinen asia, että yrität, jos löydät epälineaarinen trendi tietoja. Toisin sanoen x-arvojen muuttaminen on tarkoituksenmukaista, kun ei-lineaarisuus on ainoa ongelma (eli riippumattomuus, normaalius ja yhtä suuri varianssi-ehdot täyttyvät). Huomaa kuitenkin, että epälineaarisuus voi olla tarpeen korjata ennen kuin voit arvioida normaaliuden ja yhtä suuren varianssin oletuksia. Vaikka jotkin oletukset näyttävät pitävän paikkansa ennen muunnoksen soveltamista, ne eivät välttämättä enää päde, kun muunnosta sovelletaan. Toisin sanoen muunnosten käyttäminen on osa iteratiivista prosessia, jossa kaikki lineaariset regressiooletukset tarkistetaan uudelleen jokaisen iteraation jälkeen.
muista, että vaikka keskitymme tässä yksinkertaiseen lineaariseen regressiomalliin, olennaiset ajatukset pätevät yleisemmin myös useisiin lineaarisiin regressiomalleihin. Voimme harkita muuttamassa mitään ennustajat tutkimalla scatterplots, jäännökset vs. kukin ennustaja vuorollaan.
mallin rakentaminen
esimerkki. Helpoin tapa oppia datamuunnoksista on esimerkki. Mietitäänpä tietoja muistinsäilytyskokeesta, jossa 13 koehenkilöä pyydettiin opettelemaan ulkoa lista irrallisista esineistä. Koehenkilöitä pyydettiin sen jälkeen muistelemaan kohteita eri aikoina jopa viikkoa myöhemmin. Eri aikoina (X = aika, minuuteissa) oikein muistettujen kohteiden osuus (wordrecall) kirjattiin muistiin (wordrecall.txt)ja piirretään. Tunnustaen, että ei ole mitään hyvää syytä siihen, että virhetermit eivät olisi riippumattomia, arvioikaamme mallin jäljellä olevia kolmea ehtoa — lineaarisuutta, normaaliutta ja yhtä suuria variansseja.
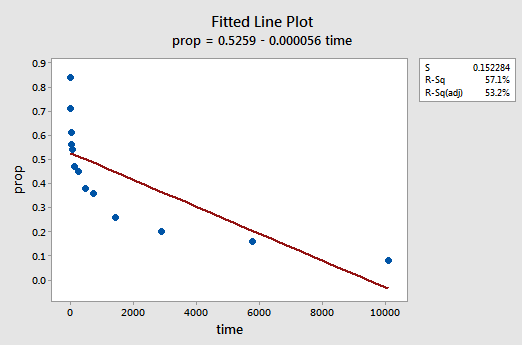
tuloksena oleva sovitetun rivin kuvaaja viittaa siihen, että takaisinkutsuttujen erien osuus (y) ei ole lineaarisesti suhteessa aikaan (x):
the residuals vs. fits plot myös viittaa siihen, että suhde ei ole lineaarinen:
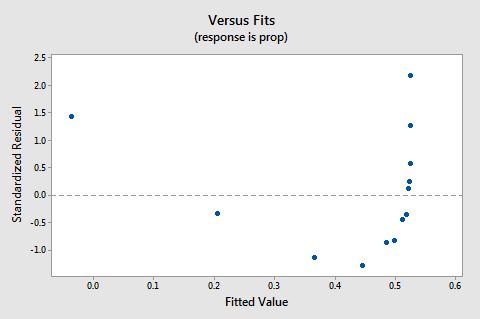
koska lineaarisuuden puute hallitsee kuviota, emme voi käyttää kuviota arvioidaksemme, ovatko virhevarianssit yhtä suuret. Meidän on korjattava epälineaarisuusongelma ennen kuin voimme arvioida oletusta yhtäläisistä variansseista.
entä jäännösten normaali todennäköisyyslaskenta? Mitä se ehdottaa virhetermeistä? Voimmeko päätellä, että ne jaetaan normaalisti?
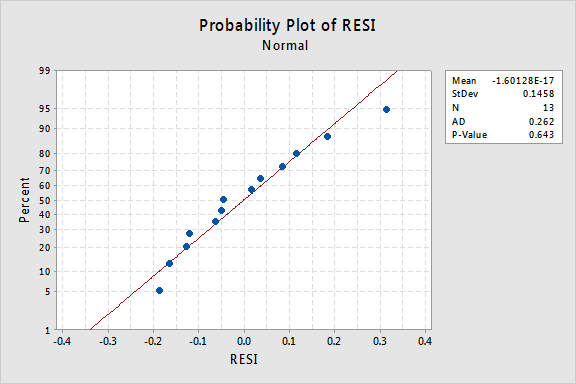
Anderson-Darlingin P-arvo tälle esimerkille on 0,643, mikä viittaa siihen, että emme hylkää normaalien virhetermien nollahypoteesia. Ei ole tarpeeksi näyttöä siitä, että virhetermit eivät olisi normaaleja.
tiivistettynä meillä on tietojoukko, jossa epälineaarisuus on ainoa suuri ongelma. Tämä tilanne huutaa muuttaa vain ennustajan arvot. Ennen kuin teemme niin, otetaan syrjään ja keskustella ”logaritminen transformaatio,” koska se on yleisin ja hyödyllisin data transformation saatavilla.
logaritminen muunnos. Oletuslogaritmisessa muunnoksessa otetaan vain kunkin tietoarvon luonnollinen logaritmi — merkitään Ln tai loge tai yksinkertaisesti log. Voidaan harkita toisenlaista logaritmia, kuten log base 10 tai log base 2. Luonnollinen logaritmi-joka voidaan kuitenkin ajatella logaritmina E, jossa e on vakio 2,718282… – on yleisin tieteellisessä työssä käytetty logaritminen asteikko.
luonnollisen logaritmisen funktion yleiset ominaisuudet ovat:
- X: n luonnollinen logaritmi on potenssi e = 2,718282… tämä voidaan todeta notaarisesti, koska Ln (ex) = x. esimerkiksi 5: n luonnollinen logaritmi on potenssi, johon on nostettava e = 2.718282… saadakseen 5. Koska 2.7182821.60944 on noin 5, sanomme, että luonnollinen logaritmi 5 on 1.60944. Notaarisesti sanomme ln (5) = 1.60944.
- E: n luonnollinen logaritmi on yhtä suuri kuin yksi, eli ln(e) = 1.
- yhden luonnollinen logaritmi on yhtä suuri kuin nolla Eli Ln(1) = 0.
luonnollisen logaritmifunktion kuvaaja:
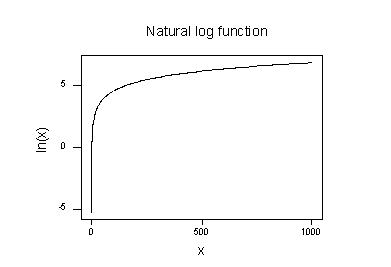
viittaa siihen, että luonnollisen logaritmin muunnoksen vaikutukset ovat:
- pienet arvot, jotka ovat lähekkäin, leviävät kauemmas.
- suuret hajaantuneet arvot tuodaan lähemmäksi toisiaan.
takaisin esimerkkiin. Käytetään luonnollista logaritmia x-arvojen muuttamiseen muistin säilyttämisen kokeessa. Koska X = aika on ennustaja, meidän tarvitsee vain ottaa luonnollinen logaritmi jokaisesta aika-arvosta, joka esiintyy tietojoukossa. Näin luomme uuden ennusteen nimeltä lntime:
| time | prop | lntime |
| 1 | 0, 84 | |
| 5 | 0.71 | 1.60944 |
| 15 | 0.61 | 2.70805 |
| 30 | 0.56 | 3.40120 |
| 60 | 0.54 | 4.09434 |
| 120 | 0.47 | 4.78749 |
| 240 | 0.45 | 5.48064 |
| 480 | 0.38 | 6.17379 |
| 720 | 0.36 | 6.57925 |
| 1440 | 0.26 | 7.27240 |
| 2880 | 0.20 | 7.96555 |
| 5760 | 0.16 | 8.65869 |
| 10080 | 0.08 | 9.21831 |
We take the natural logarithm for each value of time and place the results in their own column. Eli me ”muunnamme” jokaisen ennustajan aika-arvoksi Ln(aika). Esimerkiksi Ln(1) = 0, ln(5) = 1.60944 ja ln (15) = 2.70805 ja niin edelleen.
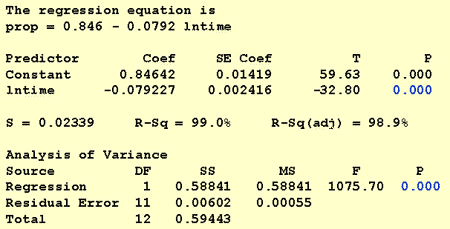
nyt kun olemme muuttaneet ennustajan arvoja, katsotaan Auttoiko se korjaamaan epälineaarista trendiä aineistossa. Sovitamme mallin uudelleen niin, että Y = prop on vastaus ja X = lntime on ennustaja.
tuloksena oleva sovitetun viivan kuvaaja viittaa siihen, että predikaattoriarvojen luonnollisen logaritmin ottaminen on hyödyllistä.
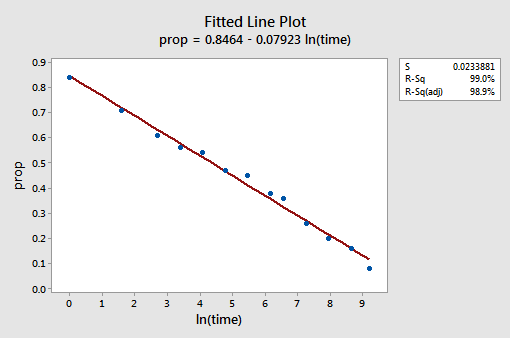
itse asiassa R2-arvo on noussut 57,1%: sta 99,0%: iin. Se kertoo, että 99 prosenttia palautettujen sanojen osuuden vaihtelusta (prop) vähenee, kun otetaan huomioon ajan luonnollinen loki (lntime)!
Uusi jäännös vs. fits-kuvaaja osoittaa merkittävää parannusta verrattuna kääntämättömiin tietoihin perustuvaan kuvaajaan.
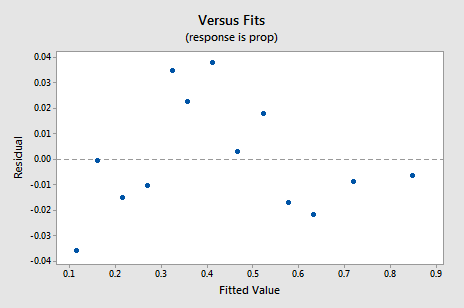
saatat huolestua jonkinlaisesta ylös-alas suhdannevaihtelusta havaintoalalla. Varoitan teitä jälleen siitä, että näitä juonia ei pidä tulkita liikaa, varsinkin kun tietokokonaisuus on näin pieni. Sinun ei todellakaan pitäisi odottaa täydellisyyttä, kun turvaudut ottamaan datamuunnoksia. Joskus täytyy vain tyytyä merkittäviin parannuksiin. Muuten, juoni myös antaa ymmärtää, että on OK olettaa, että virhevarianssit ovat yhtä suuret.
jäännösten normaali todennäköisyyslaskenta osoittaa, että x-arvojen muuttamisella ei ollut vaikutusta virhetermien normaaliuteen:
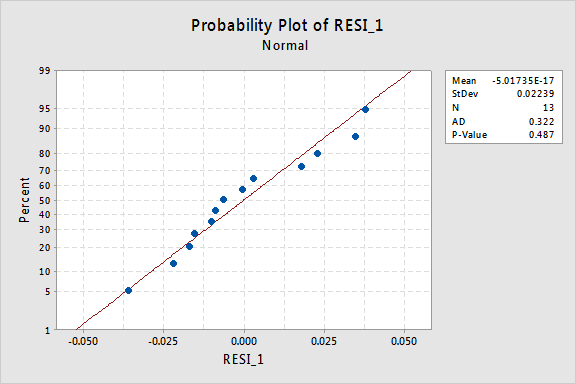
jälleen Andersonin-Darlingin P-arvo on suuri, joten emme voi hylätä normaalien virhetermien nollahypoteesia. Ei ole tarpeeksi näyttöä siitä, että virhetermit eivät olisi normaaleja.
Mitä jos olisimme muuttaneet y-arvot sen sijaan? Aiemmin sanoin, että vaikka jotkut oletukset saattavat näyttää pitävän ennen muutoksen soveltamista, ne eivät välttämättä enää pidä, kun muutos on sovellettu. Jos esimerkiksi virhetermit ovat hyvin käyttäytyviä, y-arvojen muuttaminen voisi muuttaa ne huonosti käyttäytyviksi virhetermeiksi. Virhetermit muistin säilyttämistiedoille ennen x-arvojen muuttamista näyttävät hyväkäytöksisiltä (siinä mielessä, että ne näyttävät suunnilleen normaaleilta). Siksi voidaan olettaa, että Y-arvojen muuttaminen x-arvojen sijaan voisi aiheuttaa virhetermien huonokäytöksisyyden. Katsotaanpa vilkaista muistin säilyttäminen tiedot nähdä esimerkki siitä, mitä voi tapahtua, kun muutamme y-arvot, kun ei-lineaarisuus on ainoa ongelma.
yrityksen ja erehdyksen kautta huomaamme, että Y: n voimanmuutos, joka parhaiten korjaa epälineaarisuuden, on y-1,25. Fixed line-juoni havainnollistaa, että transformaatio todellakin suoristaa suhdetta — tosin ei yhtä hyvin kuin x-arvojen log-transformaatio.
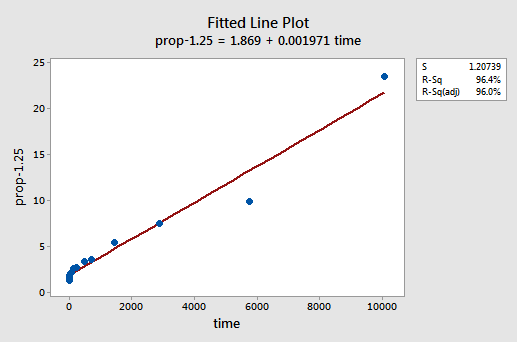
huomaa, että R2-arvo on noussut 57,1%: sta 96,4%: iin.
jäännökset osoittavat parannusta ei-lineaarisuuden suhteen, joskaan parannus ei ole suuri…
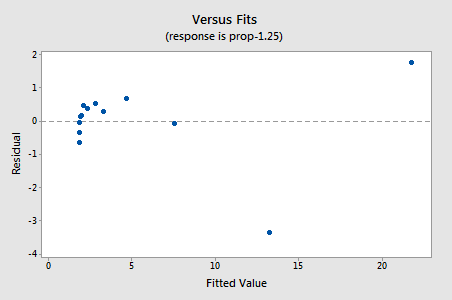
…mutta nyt meillä on normaalista poikkeavat virhetermit! Andersonin-Darlingin p-arvo on alle 0,005, joten hylkäämme normaalien virhetermien nollahypoteesin. On riittävästi näyttöä siitä, että virhetermit eivät ole normaaleja:
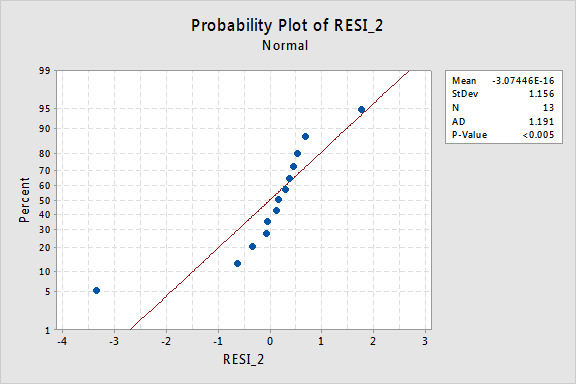
jälleen, jos virhetermit käyttäytyvät hyvin ennen muunnosta, y-arvojen muuttaminen voi muuttaa ne huonosti käyttäytyviksi virhetermeiksi.
käyttämällä mallia
kun olemme löytäneet parhaan mallin regressioaineistollemme, Voimme käyttää mallia vastataksemme kiinnostaviin tutkimuskysymyksiimme. Jos mallimme sisältää muunnettuja ennustusarvoja (x), saatamme joutua tekemään pieniä muutoksia jo oppimiimme standardimenetelmiin.
käytetään lineaarista regressiomalliamme muistinvarmistustiedon osalta—y = prop vasteena ja X = lntime ennustajana—vastataksemme neljään eri tutkimuskysymykseen.
tutkimuskysymys #1: Mikä on muistamisen jälkeisen ajan ja muistamisen tehokkuuden välinen yhteys?
vastataksemme tähän tutkimuskysymykseen kuvailemme vain suhteen luonnetta. Toisin sanoen oikein muistettujen sanojen osuus liittyy negatiivisesti lineaarisesti ajan luonnolliseen lokiin sanojen ulkoa opettelun jälkeen. Ei ole yllättävää, että ajan luonnollisen lokin lisääntyessä muistettujen sanojen osuus vähenee.
tutkimuskysymys #2: Onko muistamisen jälkeisen ajan ja muistamisen tehokkuuden välillä yhteyttä?
tähän tutkimuskysymykseen vastattaessa standardimenetelmää ei tarvitse muuttaa. Testaamme vain nollahypoteesia H0: β1 = 0 joko F-testillä tai vastaavalla t-testillä:
kuten ohjelmistotulos havainnollistaa, p-arvo on < 0,001. On merkittävää näyttöä 0.05 taso päätellä, että on olemassa lineaarinen assosiaatio osuus sanoja muistutti ja luonnollinen log aikaa vuodesta ulkoa.
tutkimuskysymys #3: minkä osuuden sanoista voimme odottaa satunnaisesti valitun henkilön muistavan 1000 minuutin jälkeen?
meidän tarvitsee vain laskea ennustusväli — yhdellä pienellä muutoksella — vastataksemme tähän tutkimuskysymykseen. Ennustemuuttujamme on ajan luonnollinen loki. Siksi, kun käytämme tilastollisia ohjelmistoja ennustusvälin laskemiseen, meidän on varmistettava, että määritämme ennustusarvojen arvon muunnetuissa yksiköissä, ei alkuperäisissä yksiköissä. 1000 minuutin luonnollinen hirsi on 6,91 hirsiminuuttia. Käyttämällä ohjelmistoa laskemaan 95%: n ennustusväli, kun lntime = 6.91, saadaan:
tuotos kertoo, että voimme olla 95% varmoja, että, kun 1000 minuuttia, satunnaisesti valittu henkilö muistaa välillä 24,5% ja 35.3% sanoista.
tutkimuskysymys #4: Kuinka paljon odotettu takaisinkutsu muuttuu, jos aika kymmenkertaistuu?
Jos asiaa ajattelee, tähän tutkimuskysymykseen vastaaminen tarkoittaa vain kulmakertoimen β1 arvioimista ja tulkitsemista. No, ei ihan-pientä säätöä on. Yleensä ennusteen x K-kertaistumiseen liittyy:
β1 × Ln(k)
muutos vasteen keskiarvossa y.
Tämä seuraava derivointi saattaa auttaa ymmärtämään ja siksi muistamaan tämän kaavan.
toisin sanoen x: n kymmenkertaistuminen liittyy Y: n keskiarvon β1 × ln(10) muutokseen. ja x: n kaksinkertainen kasvu liittyy Y: n keskiarvon β1 × Ln(2) muutokseen.
yleisesti ottaen tulisi käyttää vain mallin laajuuden kannalta järkeviä K: n kerrannaisia. Esimerkiksi, jos x-arvot tietojoukossasi vaihtelevat 2: sta 8: aan, on vain järkevää harkita k-kerrannaisia, jotka ovat 4: ää tai pienempiä. Jos X: n arvo olisi 2, kymmenkertainen korotus (eli k = 10) veisi 2: sta 2 × 10 = 20: een, joka on mallin soveltamisalan ulkopuolinen arvo. Muistinmenetysaineistossa ennustearvot vaihtelevat 1: stä 10080: een, joten kymmenkertaistamisen harkitseminen ei ole ongelma.
Jos olemme kiinnostuneita vain piste-estimaatin saamisesta, otamme vain slope-parametrin (b1 = -0.079227) estimaatin ohjelmistotuloksesta:

ja kerromme sen ln(10):
B1 × ln(10) = -0.079227 × ln(10) = -0.182
odotamme takaisinkutsuttujen sanojen prosenttiosuuden pienenevän (koska merkki on negatiivinen) 18.2% jokaista kymmenkertaista lisäystä muistamisen jälkeisessä ajassa.
tästä piste-arviosta on tosin vain vähän hyötyä. Kuinka varmoja voimme olla siitä, että arvio on lähellä todellista tuntematonta arvoa? Luonnollisesti pitäisi laskea 95 prosentin varmuusväli. Tätä varten lasketaan vain 95% luottamusväli β1: lle, kuten aina: