In questa sezione, impariamo come costruire e utilizzare un semplice modello di regressione lineare trasformando i valori x predictor. Questa potrebbe essere la prima cosa che provi se trovi una tendenza non lineare nei tuoi dati. Cioè, trasformare i valori x è appropriato quando la non linearità è l’unico problema (cioè, le condizioni di indipendenza, normalità e uguale varianza sono soddisfatte). Si noti, tuttavia, che potrebbe essere necessario correggere la non linearità prima di poter valutare la normalità e le ipotesi di varianza uguale. Inoltre, mentre alcune ipotesi possono sembrare valide prima di applicare una trasformazione, potrebbero non essere più valide una volta applicata una trasformazione. In altre parole, l’utilizzo delle trasformazioni fa parte di un processo iterativo in cui tutte le ipotesi di regressione lineare vengono ricontrollate dopo ogni iterazione.
Tieni presente che sebbene ci stiamo concentrando su un semplice modello di regressione lineare qui, le idee essenziali si applicano più in generale anche a più modelli di regressione lineare. Possiamo considerare la possibilità di trasformare uno qualsiasi dei predittori esaminando i grafici a dispersione dei residui rispetto a ciascun predittore a turno.
Costruire il modello
Un esempio. Il modo più semplice per conoscere le trasformazioni dei dati è l’esempio. Consideriamo i dati di un esperimento di conservazione della memoria in cui a 13 soggetti è stato chiesto di memorizzare un elenco di elementi disconnessi. Ai soggetti è stato quindi chiesto di richiamare gli articoli in vari momenti fino a una settimana dopo. La proporzione di elementi (y = prop) richiamati correttamente in vari momenti (x = tempo, in minuti) da quando l’elenco è stato memorizzato è stata registrata (wordrecall.txt) e tracciata. Riconoscendo che non c’è una buona ragione per cui i termini di errore non sarebbero indipendenti, valutiamo le restanti tre condizioni — linearità, normalità e uguali varianze — del modello.
La trama della linea montata risultante suggerisce che la proporzione di elementi richiamati (y) non è linearmente correlata al tempo (x):
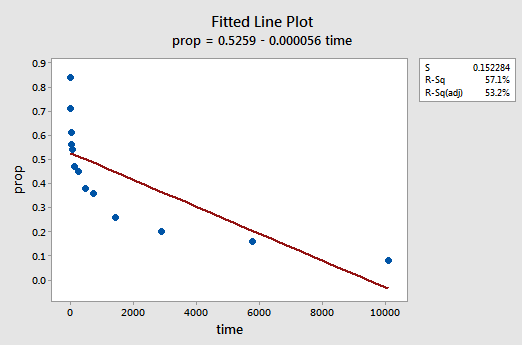
I residui vs adatta trama suggerisce, inoltre, che la relazione non è lineare:
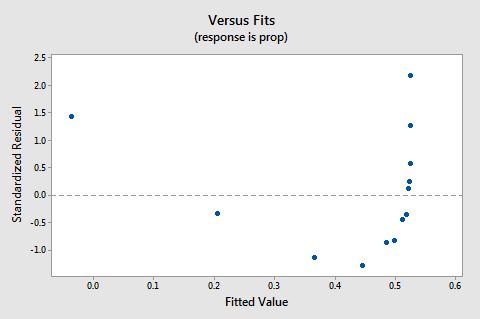
a Causa della mancanza di linearità domina la trama non è possibile utilizzare il terreno per valutare o meno l’errore varianze sono uguali. Dobbiamo risolvere il problema della non linearità prima di poter valutare l’ipotesi di variazioni uguali.
Che dire della normale trama di probabilità dei residui? Cosa suggerisce sui termini di errore? Possiamo concludere che sono normalmente distribuiti?
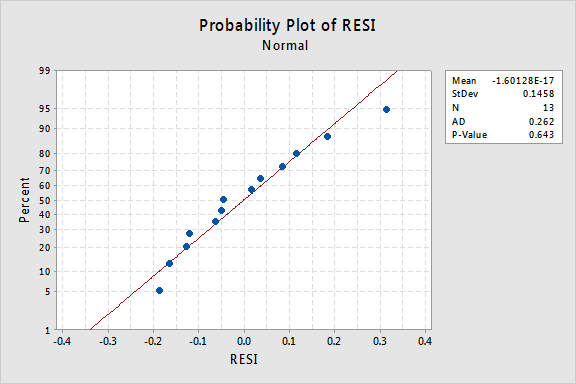
Il valore P di Anderson-Darling per questo esempio è 0.643, il che suggerisce che non riusciamo a rifiutare l’ipotesi nulla dei termini di errore normali. Non ci sono prove sufficienti per concludere che i termini degli errori non sono normali.
In sintesi, abbiamo un set di dati in cui la non linearità è l’unico problema principale. Questa situazione urla per trasformare solo i valori del predittore. Prima di farlo, prendiamo da parte e discutiamo la “trasformazione logaritmica”, poiché è la trasformazione dei dati più comune e più utile disponibile.
La trasformazione logaritmica. La trasformazione logaritmica predefinita consiste semplicemente nel prendere il logaritmo naturale-denotato ln o loge o semplicemente log-di ciascun valore di dati. Si potrebbe prendere in considerazione un diverso tipo di logaritmo, come log base 10 o log base 2. Tuttavia, il logaritmo naturale-che può essere pensato come log base e dove e è la costante 2.718282… – è la scala logaritmica più comune utilizzata nel lavoro scientifico.
Le caratteristiche generali della funzione logaritmica naturale sono:
- Il logaritmo naturale di x è la potenza di e = 2.718282… che devi prendere per ottenere x. Questo può essere dichiarato notazionalmente come ln ( ex) = x. Ad esempio, il logaritmo naturale di 5 è la potenza a cui devi aumentare e = 2.718282… al fine di ottenere 5. Poiché 2.7182821.60944 è circa 5, diciamo che il logaritmo naturale di 5 è 1.60944. Notazionalmente, diciamo ln (5) = 1.60944.
- Il logaritmo naturale di e è uguale a uno, cioè ln(e) = 1.
- Il logaritmo naturale di uno è uguale a zero, cioè ln(1) = 0.
La trama del logaritmo naturale funzione:
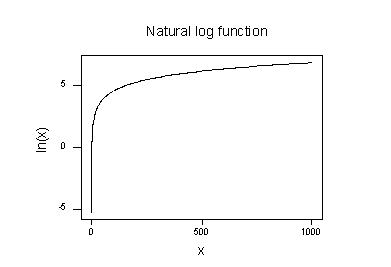
suggerisce che gli effetti di prendere la naturale trasformazione logaritmica sono:
- Piccoli valori che sono vicini, sono l’ulteriore diffusione fuori.
- I grandi valori che vengono distribuiti vengono avvicinati.
Torna all’esempio. Usiamo il logaritmo naturale per trasformare i valori x nei dati dell’esperimento di conservazione della memoria. Poiché x = time è il predittore, tutto ciò che dobbiamo fare è prendere il logaritmo naturale di ogni valore temporale che appare nel set di dati. In tal modo, si crea un nuovo trasformato predittore chiamato lntime:
| tempo | prop | lntime |
| 1 | 0.84 | 0.00000 |
| 5 | 0.71 | 1.60944 |
| 15 | 0.61 | 2.70805 |
| 30 | 0.56 | 3.40120 |
| 60 | 0.54 | 4.09434 |
| 120 | 0.47 | 4.78749 |
| 240 | 0.45 | 5.48064 |
| 480 | 0.38 | 6.17379 |
| 720 | 0.36 | 6.57925 |
| 1440 | 0.26 | 7.27240 |
| 2880 | 0.20 | 7.96555 |
| 5760 | 0.16 | 8.65869 |
| 10080 | 0.08 | 9.21831 |
We take the natural logarithm for each value of time and place the results in their own column. Cioè, “trasformiamo” ogni valore di tempo predittore in un valore ln(tempo). Ad esempio, ln(1) = 0, ln(5) = 1.60944 e ln(15) = 2.70805 e così via.
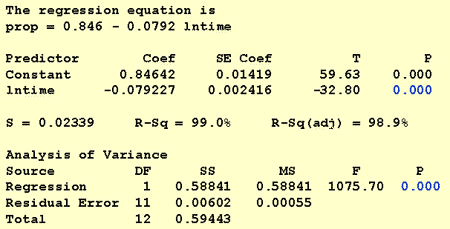
Ora che abbiamo trasformato i valori dei predittori, vediamo se ha aiutato a correggere la tendenza non lineare nei dati. Riadattiamo il modello con y = prop come risposta e x = lntime come predittore.
Il diagramma di linea montato risultante suggerisce che prendere il logaritmo naturale dei valori predittori è utile.
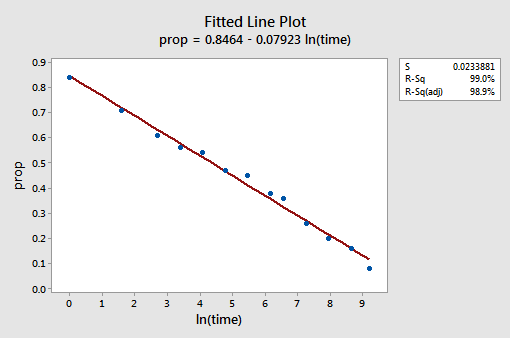
In effetti, il valore R2 è aumentato dal 57,1% al 99,0%. Ci dice che il 99% della variazione nella proporzione di parole richiamate (prop) viene ridotta tenendo conto del log naturale del tempo (lntime)!
Il nuovo grafico residual vs. fits mostra un miglioramento significativo rispetto a quello basato sui dati non tradotti.
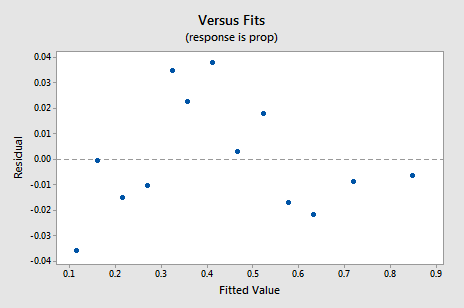
Potresti essere preoccupato per una sorta di tendenza ciclica up-down nella trama. Ti avverto di nuovo a non interpretare eccessivamente questi grafici, specialmente quando il set di dati è piccolo come questo. Non dovresti davvero aspettarti la perfezione quando ricorri alle trasformazioni dei dati. A volte devi solo accontentarti di miglioramenti significativi. A proposito, la trama suggerisce anche che è giusto supporre che le varianze di errore siano uguali.
Il diagramma di probabilità normale dei residui mostra che la trasformazione dei valori x non ha avuto alcun effetto sulla normalità dei termini di errore:
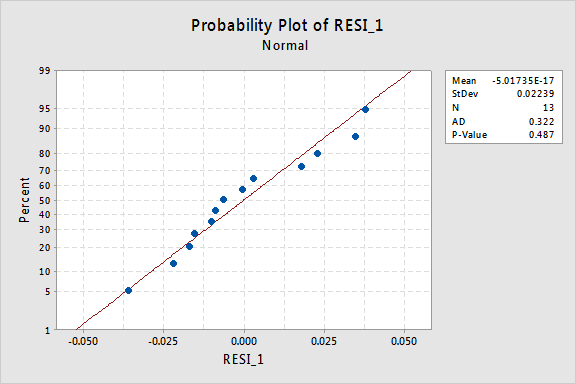
Ancora una volta il valore P di Anderson-Darling è grande, quindi non riusciamo a rifiutare l’ipotesi nulla dei termini di errore normali. Non ci sono prove sufficienti per concludere che i termini degli errori non sono normali.
E se invece avessimo trasformato i valori y? In precedenza ho detto che mentre alcune ipotesi possono sembrare valide prima di applicare una trasformazione, potrebbero non essere più valide una volta applicata una trasformazione. Ad esempio, se i termini di errore sono ben educati, la trasformazione dei valori y potrebbe modificarli in termini di errore mal comportati. I termini di errore per i dati di conservazione della memoria prima di trasformare i valori x sembrano essere ben educati (nel senso che appaiono approssimativamente normali). Pertanto, potremmo aspettarci che la trasformazione dei valori y anziché dei valori x possa causare un comportamento scorretto dei termini di errore. Diamo una rapida occhiata ai dati di conservazione della memoria per vedere un esempio di ciò che può accadere quando trasformiamo i valori y quando la non linearità è l’unico problema.
Per tentativi ed errori, scopriamo che la trasformazione di potenza di y che fa il miglior lavoro nel correggere la non linearità è y-1.25. La trama della linea montata illustra che la trasformazione raddrizza effettivamente la relazione, anche se certamente non così come la trasformazione del registro dei valori x.
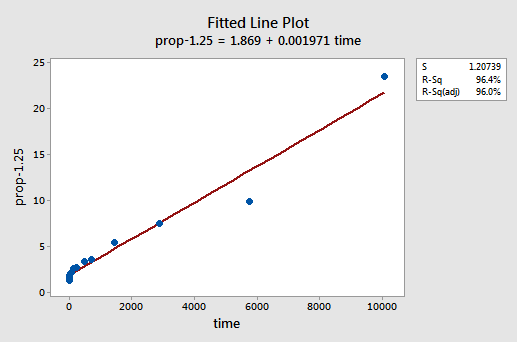
Si noti che il valore R2 è aumentato dal 57,1% al 96,4%.
I residui mostrano un miglioramento rispetto alla non linearità, anche se il miglioramento non è grande…
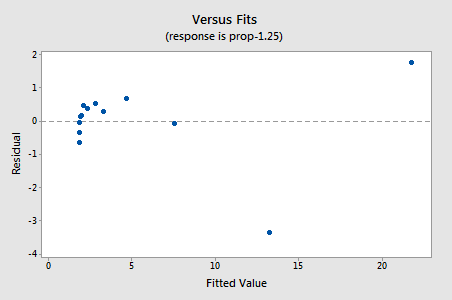
…ma ora abbiamo termini di errore non normali! Il valore P di Anderson-Darling è inferiore a 0,005, quindi rifiutiamo l’ipotesi nulla dei termini di errore normali. Ci sono prove sufficienti per concludere che i termini di errore non sono normali:
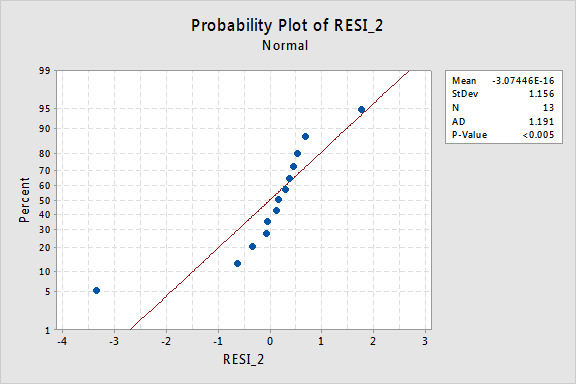
Ancora una volta, se i termini di errore sono ben comportati prima della trasformazione, trasformando i valori y possono cambiarli in termini di errore mal comportati.
Utilizzando il modello
Una volta trovato il modello migliore per i nostri dati di regressione, possiamo quindi utilizzare il modello per rispondere alle nostre domande di ricerca di interesse. Se il nostro modello comporta valori di predittore (x) trasformati, potremmo o meno dover apportare lievi modifiche alle procedure standard che abbiamo già appreso.
Usiamo il nostro modello di regressione lineare per i dati di conservazione della memoria—con y = prop come risposta e x = lntime come predittore—per rispondere a quattro diverse domande di ricerca.
Domanda di ricerca #1: Qual è la natura dell’associazione tra il tempo memorizzato e l’efficacia del richiamo?
Per rispondere a questa domanda di ricerca, descriviamo semplicemente la natura della relazione. Cioè, la proporzione di parole correttamente richiamate è negativamente linearmente correlata al registro naturale del tempo da quando le parole sono state memorizzate. Non sorprende che, con l’aumentare del log naturale del tempo, la proporzione di parole richiamate diminuisca.
Domanda di ricerca #2: esiste un’associazione tra il tempo memorizzato e l’efficacia del richiamo?
Nel rispondere a questa domanda di ricerca, non è necessaria alcuna modifica alla procedura standard. Testiamo semplicemente l’ipotesi nulla H0: β1 = 0 usando il test F o il test t equivalente:
Come illustra l’output del software, il valore P è < 0.001. Ci sono prove significative al 0.05 livello per concludere che esiste un’associazione lineare tra la proporzione di parole richiamate e il registro naturale del tempo memorizzato.
Domanda di ricerca # 3: Quale proporzione di parole possiamo aspettarci che una persona selezionata a caso richiami dopo 1000 minuti?
Abbiamo solo bisogno di calcolare un intervallo di previsione — con una leggera modifica — per rispondere a questa domanda di ricerca. La nostra variabile predittiva è il log naturale del tempo. Pertanto, quando utilizziamo un software statistico per calcolare l’intervallo di previsione, dobbiamo assicurarci di specificare il valore dei valori predittivi nelle unità trasformate, non nelle unità originali. Il log naturale di 1000 minuti è di 6,91 log-minuti. Utilizzando il software per calcolare un intervallo di previsione del 95% quando lntime = 6.91, otteniamo:
L’output ci dice che possiamo essere sicuri al 95% che, dopo 1000 minuti, una persona selezionata a caso richiamerà tra 24.5% e 35.3% delle parole.
Domanda di ricerca # 4: Quanto cambia il richiamo previsto se il tempo aumenta di dieci volte?
Se ci pensate, rispondere a questa domanda di ricerca implica semplicemente stimare e interpretare il parametro di pendenza β1. Beh, non proprio-c’è una leggera regolazione. In generale, un aumento di k-fold nel predittore x è associato a:
β1 × ln(k)
cambiamento nella media della risposta y.
Questa derivazione che segue potrebbe aiutarti a capire e quindi ricordare questa formula.
Cioè, un aumento di dieci volte di x è associato a un cambiamento β1 × ln(10) nella media di y. E, un aumento di due volte di x è associato a un cambiamento β1 × ln(2) nella media di y.
In generale, dovresti usare solo multipli di k che abbiano senso per l’ambito del modello. Ad esempio, se i valori x nel set di dati vanno da 2 a 8, ha senso solo considerare i multipli k che sono 4 o più piccoli. Se il valore di x fosse 2, un aumento di dieci volte (cioè k = 10) ti porterebbe da 2 a 2 × 10 = 20, un valore al di fuori dell’ambito del modello. Nel set di dati di conservazione della memoria, i valori del predittore vanno da 1 a 10080, quindi non vi è alcun problema con la considerazione di un aumento di dieci volte.
Se si è interessati solo a ottenere un punto di stima, ci si limita a prendere la stima della pendenza parametro (b1 = -0.079227) dal software di uscita:

e moltiplicarlo per ln(10):
b1 × ln(10) = -0.079227 × ln(10) = -0.182
Ci aspettiamo che la percentuale di ha ricordato le parole a diminuire (dal momento che il segno è negativo) 18.2% per ogni aumento di dieci volte nel tempo trascorso dalla memorizzazione.
Naturalmente, questa stima puntuale è di utilità limitata. Quanto possiamo essere sicuri che la stima sia vicina al vero valore sconosciuto? Naturalmente, dovremmo calcolare un intervallo di confidenza del 95%. Per fare ciò, calcoliamo solo un intervallo di confidenza del 95% per β1 come abbiamo sempre: