în această secțiune, învățăm cum să construim și să folosim un model simplu de regresie liniară prin transformarea valorilor predictorului X. Acesta ar putea fi primul lucru pe care îl încercați dacă găsiți o tendință neliniară în datele dvs. Adică transformarea valorilor x este adecvată atunci când neliniaritatea este singura problemă (adică sunt îndeplinite condițiile de Independență, normalitate și variație egală). Rețineți, totuși, că poate fi necesar să corectați neliniaritatea înainte de a putea evalua normalitatea și ipotezele de variație egală. De asemenea, în timp ce unele ipoteze pot părea valabile înainte de aplicarea unei transformări, ele nu mai pot fi valabile odată ce se aplică o transformare. Cu alte cuvinte, utilizarea transformărilor face parte dintr-un proces iterativ în care toate ipotezele de regresie liniară sunt re-verificate după fiecare iterație.
rețineți că, deși ne concentrăm pe un model simplu de regresie liniară aici, ideile esențiale se aplică mai general și modelelor de regresie liniară multiplă. Putem lua în considerare transformarea oricăruia dintre predictori prin examinarea scatterplots a reziduurilor față de fiecare predictor la rândul său.
construirea modelului
Un exemplu. Cel mai simplu mod de a afla despre transformările de date este prin exemplu. Să luăm în considerare datele dintr-un experiment de retenție a memoriei în care 13 subiecți au fost rugați să memoreze o listă de elemente deconectate. Subiecții au fost apoi rugați să-și amintească articolele la diferite momente până la o săptămână mai târziu. Proporția de elemente (y = prop) corect amintit la diferite momente (x = timp, în minute), deoarece lista a fost memorat au fost înregistrate (wordrecall.txt) și reprezentate grafic. Recunoscând că nu există niciun motiv întemeiat pentru care Termenii de eroare nu ar fi independenți, să evaluăm celelalte trei condiții — liniaritate, normalitate și diferențe egale — ale modelului.
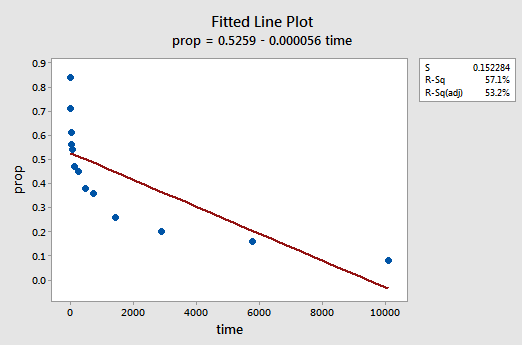
graficul de linie montat rezultat sugerează că proporția elementelor rechemate (y) nu este legată liniar de timp (x):
reziduuri vs.fits plot sugerează, de asemenea, că relația nu este liniară:
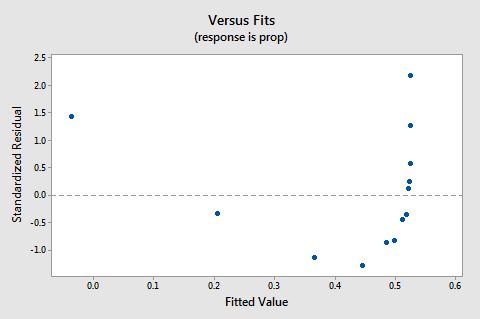
deoarece lipsa de liniaritate domină plot, nu putem folosi plot pentru a evalua dacă sau nu varianțele de eroare sunt egale. Trebuie să rezolvăm problema neliniarității înainte de a putea evalua presupunerea unor diferențe egale.cum rămâne cu probabilitatea normală a reziduurilor? Ce sugerează despre termenii de eroare? Putem concluziona că acestea sunt distribuite în mod normal?
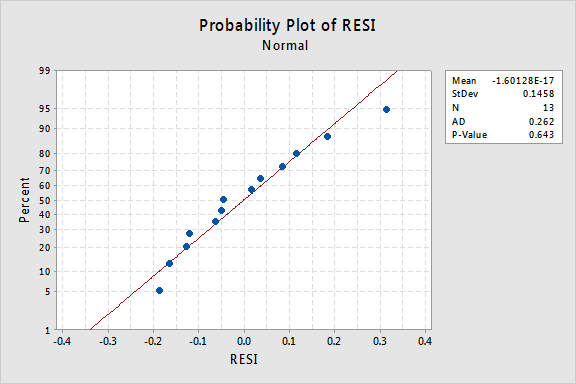
valoarea p Anderson-Darling pentru acest exemplu este 0,643, ceea ce sugerează că nu reușim să respingem ipoteza nulă a Termenilor normali de eroare. Nu există suficiente dovezi pentru a concluziona că termenii erorilor nu sunt normali.în rezumat, avem un set de date în care non-liniaritatea este singura problemă majoră. Această situație strigă pentru transformarea doar a valorilor predictorului. Înainte de a face acest lucru, să luăm o parte și să discutăm despre „transformarea logaritmică”, deoarece este cea mai comună și mai utilă transformare a datelor disponibile.transformarea logaritmică. Transformarea logaritmică implicită implică doar luarea logaritmului natural-notat ln sau loge sau pur și simplu log — a fiecărei valori de date. S-ar putea lua în considerare luarea unui alt tip de logaritm, cum ar fi log base 10 sau log base 2. Cu toate acestea, logaritmul natural — care poate fi gândit ca bază de jurnal e unde e este constanta 2.718282… – este cea mai comună scară logaritmică utilizată în activitatea științifică.
caracteristicile generale ale funcției logaritmice naturale sunt:
- logaritmul natural al lui x este puterea lui e = 2.718282… că trebuie să luați pentru a obține x. Acest lucru poate fi declarat notațional ca Ln(ex) = x. de exemplu, logaritmul natural al lui 5 este puterea la care trebuie să ridicați e = 2.718282… pentru a obține 5. Deoarece 2.7182821.60944 este de aproximativ 5, spunem că logaritmul natural al lui 5 este 1.60944. Notațional, spunem ln (5) = 1.60944.
- logaritmul natural al lui e este egal cu unul, adică ln ( e) = 1.
- logaritmul natural al unuia este egal cu zero, adică ln (1) = 0.
graficul funcției logaritmice naturale:
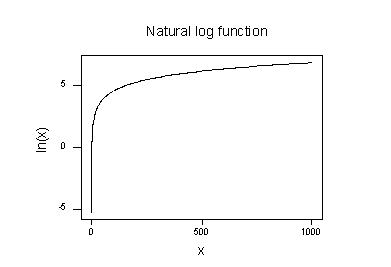
sugerează că efectele transformării logaritmice naturale sunt:
- valorile mici care sunt apropiate sunt răspândite mai departe.
- valorile mari care sunt răspândite sunt apropiate.
înapoi la exemplu. Să folosim logaritmul natural pentru a transforma valorile x în datele experimentului de retenție a memoriei. Deoarece X = timpul este predictorul, tot ce trebuie să facem este să luăm logaritmul natural al fiecărei valori de timp care apare în setul de date. În acest sens, vom crea un predictor nou transformat numit lntime:
| timp | prop | lntime |
| 1 | 0.84 | 0.00000 |
| 5 | 0.71 | 1.60944 |
| 15 | 0.61 | 2.70805 |
| 30 | 0.56 | 3.40120 |
| 60 | 0.54 | 4.09434 |
| 120 | 0.47 | 4.78749 |
| 240 | 0.45 | 5.48064 |
| 480 | 0.38 | 6.17379 |
| 720 | 0.36 | 6.57925 |
| 1440 | 0.26 | 7.27240 |
| 2880 | 0.20 | 7.96555 |
| 5760 | 0.16 | 8.65869 |
| 10080 | 0.08 | 9.21831 |
We take the natural logarithm for each value of time and place the results in their own column. Adică „transformăm” fiecare valoare a timpului predictor într-o valoare Ln(timp). De exemplu, ln(1) = 0, ln(5) = 1.60944 și ln(15) = 2.70805 și așa mai departe.
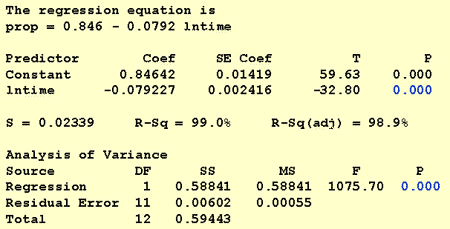
acum că am transformat valorile predictorului, să vedem dacă a ajutat la corectarea tendinței neliniare a datelor. Re-potrivim modelul cu y = prop ca răspuns și x = lntime ca predictor.
graficul de linie montat rezultat sugerează că luarea logaritmului natural al valorilor predictorului este utilă.
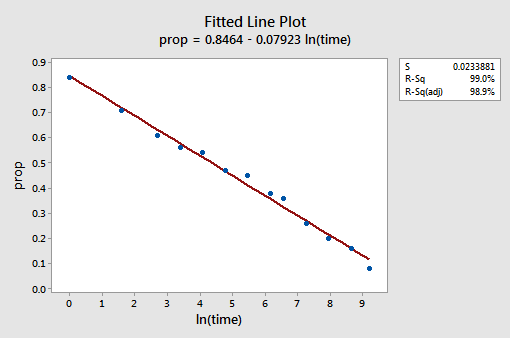
într-adevăr, valoarea R2 a crescut de la 57,1% la 99,0%. Ne spune că 99% din variația proporției cuvintelor amintite (prop) este redusă luând în considerare jurnalul natural al timpului (lntime)!
noul grafic rezidual vs.fits arată o îmbunătățire semnificativă față de cea bazată pe datele netransformate.
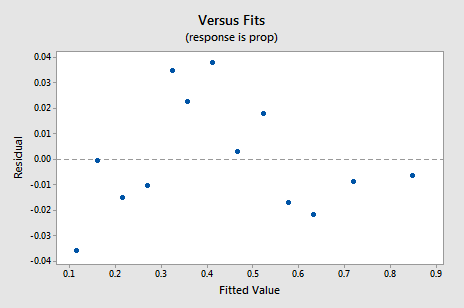
s-ar putea deveni preocupat de un fel de tendință ciclică sus-jos în plot. Vă avertizez din nou să nu interpretați excesiv aceste parcele, mai ales atunci când setul de date este mic ca acesta. Chiar nu ar trebui să vă așteptați la perfecțiune atunci când recurgeți la efectuarea transformărilor de date. Uneori trebuie doar să vă mulțumiți cu îmbunătățiri semnificative. Apropo, complotul sugerează, de asemenea, că este bine să presupunem că varianțele de eroare sunt egale.
graficul de probabilitate normală a reziduurilor arată că transformarea valorilor x nu a avut niciun efect asupra normalității termenilor de eroare:
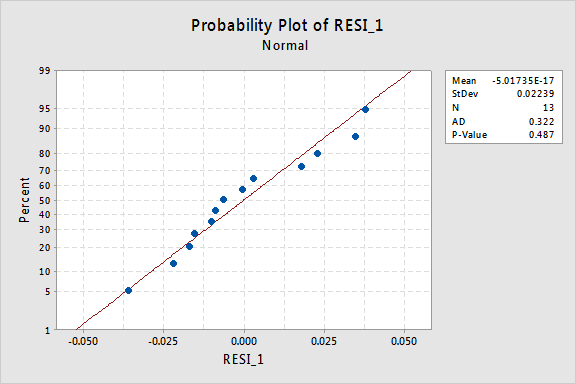
Din nou, valoarea p Anderson-Darling este mare, deci nu reușim să respingem ipoteza nulă a Termenilor normali de eroare. Nu există suficiente dovezi pentru a concluziona că termenii erorilor nu sunt normali.
Ce se întâmplă dacă am fi transformat valorile y în schimb? Mai devreme am spus că în timp ce unele ipoteze pot părea să dețină înainte de aplicarea unei transformări, ele nu mai pot deține o dată o transformare este aplicată. De exemplu, dacă termenii de eroare se comportă bine, transformarea valorilor y le-ar putea schimba în termeni de eroare cu comportament prost. Termenii de eroare pentru datele de retenție a memoriei înainte de transformarea valorilor x par să se comporte bine (în sensul că par aproximativ normale). Prin urmare, ne-am putea aștepta ca transformarea valorilor y în loc de valorile x ar putea determina termenii de eroare să se comporte prost. Să aruncăm o privire rapidă asupra datelor de retenție a memoriei pentru a vedea un exemplu despre ce se poate întâmpla atunci când transformăm valorile y atunci când neliniaritatea este singura problemă.
prin încercare și eroare, descoperim că transformarea puterii lui y care face cea mai bună treabă la corectarea neliniarității este y-1.25. Graficul liniei montate ilustrează faptul că transformarea îndreaptă într — adevăr relația-deși, desigur, nu la fel de bine ca transformarea jurnalului valorilor X.
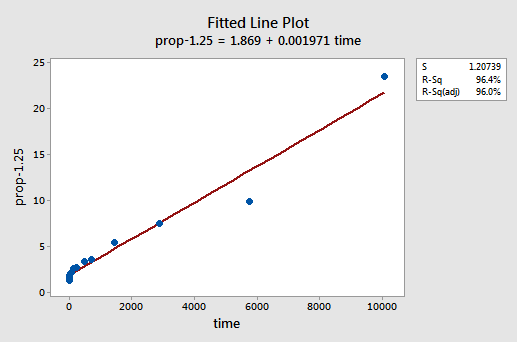
rețineți că valoarea R2 a crescut de la 57,1% la 96,4%.
reziduurile arată o îmbunătățire în ceea ce privește neliniaritatea, deși îmbunătățirea nu este mare…
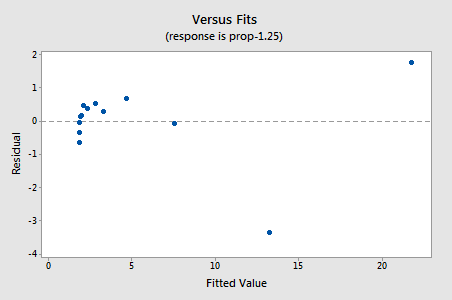
…dar acum avem Termeni de eroare non-normali! Valoarea p Anderson-Darling este mai mică de 0,005, deci respingem ipoteza nulă a Termenilor normali de eroare. Există suficiente dovezi pentru a concluziona că termenii de eroare nu sunt normali:
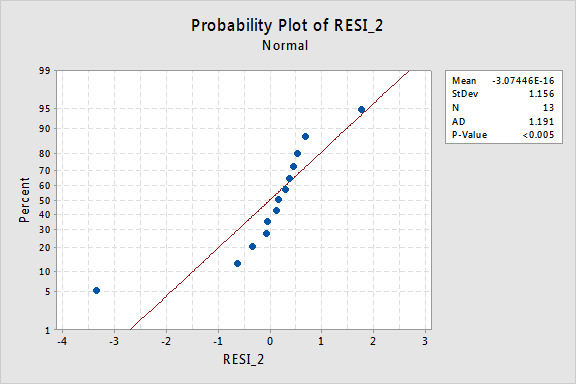
Din nou, dacă termenii de eroare sunt bine comportați înainte de transformare, transformarea valorilor y le poate schimba în termeni de eroare prost comportați.
folosind modelul
odată ce am găsit cel mai bun model pentru datele noastre de regresie, putem folosi modelul pentru a răspunde la întrebările noastre de cercetare de interes. Dacă modelul nostru implică valori predictor (x) transformate, este posibil să fie sau nu necesar să facem mici modificări la procedurile standard pe care le-am învățat deja.
să folosim modelul nostru de regresie liniară pentru datele de retenție a memoriei—cu y = prop ca răspuns și x = lntime ca predictor—pentru a răspunde la patru întrebări diferite de cercetare.
întrebarea de cercetare # 1: Care este natura asocierii dintre timpul memorat și eficacitatea rechemării?
pentru a răspunde la această întrebare de cercetare, vom descrie doar natura relației. Adică, proporția cuvintelor amintite corect este negativ liniar legată de jurnalul natural al timpului de când cuvintele au fost memorate. Nu este surprinzător că, pe măsură ce jurnalul natural al timpului crește, proporția cuvintelor amintite scade.
întrebarea de Cercetare #2: Există o asociere între timpul memorat și eficacitatea rechemării?
pentru a răspunde la această întrebare de cercetare, nu este necesară nicio modificare a procedurii standard. Noi doar testăm ipoteza nulă H0: inktific1 = 0 folosind fie testul F, fie testul t echivalent:
după cum ilustrează ieșirea software, valoarea P este < 0.001. Există dovezi semnificative la 0.05 nivel pentru a concluziona că există o asociere liniară între proporția de cuvinte amintite și jurnalul natural al timpului memorat.
întrebarea de Cercetare #3: ce proporție de cuvinte ne putem aștepta ca o persoană selectată aleatoriu să-și amintească după 1000 de minute?
trebuie doar să calculăm un interval de predicție — cu o ușoară modificare — pentru a răspunde la această întrebare de cercetare. Variabila noastră predictoare este jurnalul natural al timpului. Prin urmare, atunci când folosim software statistic pentru a calcula intervalul de predicție, trebuie să ne asigurăm că specificăm valoarea valorilor predictorului în unitățile transformate, nu în unitățile originale. Jurnalul natural de 1000 de minute este de 6,91 minute. Folosind software-ul pentru a calcula un interval de predicție de 95% atunci când lntime = 6.91, obținem:
ieșirea ne spune că putem fi 95% siguri că, după 1000 de minute, o persoană selectată aleatoriu își va aminti între 24,5% și 35.3% din cuvinte.întrebarea de Cercetare # 4: Cât de mult se schimbă rechemarea așteptată dacă timpul crește de zece ori?
dacă vă gândiți la asta, răspunsul la această întrebare de cercetare implică doar estimarea și interpretarea parametrului pantei de la 31. Ei bine, nu chiar—există o ușoară ajustare. În general, o creștere de K ori a predictorului x este asociată cu a:
XV1 ln(k)
schimbarea mediei răspunsului y.
această derivare care urmează vă poate ajuta să înțelegeți și, prin urmare, să vă amintiți această formulă.
adică, o creștere de zece ori a lui x este asociată cu o modificare a valorii medii a lui Y a lui X. și, o creștere de două ori a lui X este asociată cu o modificare a valorii medii a lui Y a lui X. 1. (2) a valorii medii a lui Y.
în general, ar trebui să utilizați numai multipli de k care au sens pentru domeniul de aplicare al modelului. De exemplu, dacă valorile x din setul dvs. de date variază de la 2 la 8, este logic să luați în considerare multiplii k care sunt 4 sau mai mici. Dacă valoarea lui x ar fi 2, o creștere de zece ori (adică, k = 10) te-ar duce de la 2 până la 2 XTX 10 = 20, o valoare în afara domeniului de aplicare al modelului. În setul de date de retenție a memoriei, valorile predictorului variază de la 1 la 10080, deci nu există nicio problemă cu luarea în considerare a unei creșteri de zece ori.
dacă suntem interesați doar să obținem o estimare a punctului, luăm doar estimarea parametrului pantei (b1 = -0.079227) din ieșirea software:

și o înmulțim cu ln(10):
B1 Ln(10) = -0.079227 Ln(10) = -0.182
ne așteptăm ca procentul de cuvinte rechemate să scadă (deoarece semnul este negativ) 18.2% pentru fiecare creștere de zece ori în timpul de când a avut loc memorarea.desigur, această estimare punctuală are o utilitate limitată. Cât de încrezători putem fi că estimarea este aproape de adevărata valoare necunoscută? Bineînțeles, ar trebui să calculăm un interval de încredere de 95%. Pentru a face acest lucru, trebuie doar să calculăm un interval de încredere de 95% pentru XV1, așa cum avem întotdeauna: