Dans cette section, nous apprenons à construire et à utiliser un modèle de régression linéaire simple en transformant les valeurs du prédicteur x. C’est peut-être la première chose que vous essayez si vous trouvez une tendance non linéaire dans vos données. Autrement dit, la transformation des valeurs x est appropriée lorsque la non-linéarité est le seul problème (c’est-à-dire que les conditions d’indépendance, de normalité et de variance égale sont remplies). Notez cependant qu’il peut être nécessaire de corriger la non-linéarité avant de pouvoir évaluer les hypothèses de normalité et de variance égale. De plus, bien que certaines hypothèses puissent sembler valables avant l’application d’une transformation, elles peuvent ne plus être valables une fois qu’une transformation est appliquée. En d’autres termes, l’utilisation de transformations fait partie d’un processus itératif où toutes les hypothèses de régression linéaire sont revérifiées après chaque itération.
Gardez à l’esprit que même si nous nous concentrons ici sur un modèle de régression linéaire simple, les idées essentielles s’appliquent également de manière plus générale aux modèles de régression linéaire multiple. Nous pouvons envisager de transformer n’importe lequel des prédicteurs en examinant tour à tour les nuages de points des résidus par rapport à chaque prédicteur.
Construction du modèle
Un exemple. La façon la plus simple d’en apprendre davantage sur les transformations de données est par l’exemple. Considérons les données d’une expérience de rétention de mémoire dans laquelle 13 sujets ont été invités à mémoriser une liste d’éléments déconnectés. Les sujets ont ensuite été invités à rappeler les articles à divers moments jusqu’à une semaine plus tard. La proportion d’éléments (y = prop) correctement rappelés à différents moments (x = temps, en minutes) depuis que la liste a été mémorisée a été enregistrée (wordrecall.txt) et tracée. Reconnaissant qu’il n’y a aucune raison valable que les termes d’erreur ne soient pas indépendants, évaluons les trois conditions restantes — linéarité, normalité et variances égales — du modèle.
Le tracé linéaire ajusté qui en résulte suggère que la proportion d’articles rappelés (y) n’est pas linéairement liée au temps (x):
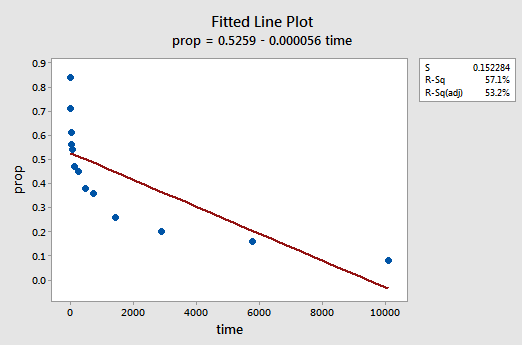
Le tracé des valeurs résiduelles par rapport aux valeurs ajustées suggère également que la relation n’est pas linéaire :
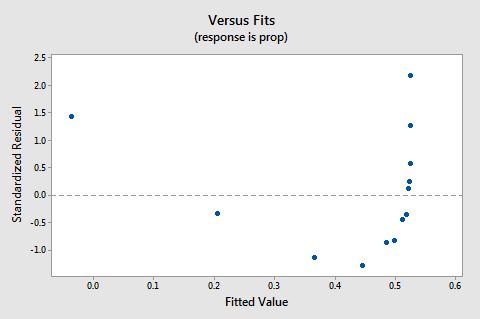
Comme le manque de linéarité domine le tracé, nous ne pouvons pas utiliser le tracé pour évaluer si les variances d’erreur sont égales ou non. Nous devons résoudre le problème de non-linéarité avant de pouvoir évaluer l’hypothèse de variances égales.
Qu’en est-il du tracé de probabilité normal des résidus? Que suggère-t-il sur les termes d’erreur? Peut-on en conclure qu’ils sont normalement distribués ?
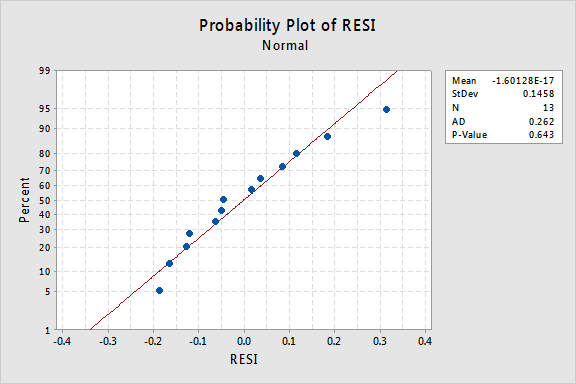
La valeur P d’Anderson-Darling pour cet exemple est 0,643, ce qui suggère que nous ne rejetons pas l’hypothèse nulle des termes d’erreur normaux. Il n’y a pas assez de preuves pour conclure que les termes d’erreurs ne sont pas normaux.
En résumé, nous avons un ensemble de données dans lequel la non-linéarité est le seul problème majeur. Cette situation crie pour ne transformer que les valeurs du prédicteur. Avant de le faire, prenons un aparté et discutons de la « transformation logarithmique », car il s’agit de la transformation de données la plus courante et la plus utile disponible.
La transformation logarithmique. La transformation logarithmique par défaut consiste simplement à prendre le logarithme naturel — noté ln ou loge ou simplement log — de chaque valeur de données. On pourrait envisager de prendre un autre type de logarithme, tel que la base de log 10 ou la base de log 2. Cependant, le logarithme naturel – qui peut être considéré comme la base log e où e est la constante 2,718282… – est l’échelle logarithmique la plus courante utilisée dans les travaux scientifiques.
Les caractéristiques générales de la fonction logarithmique naturelle sont :
- Le logarithme naturel de x est la puissance de e = 2,718282… que vous devez prendre pour obtenir x. Cela peut être indiqué notoirement comme ln(ex) = x. Par exemple, le logarithme naturel de 5 est la puissance à laquelle vous devez élever e = 2.718282… pour obtenir 5. Puisque 2.7182821.60944 est approximativement 5, nous disons que le logarithme naturel de 5 est 1.60944. Notationnellement, nous disons ln(5) = 1,60944.
- Le logarithme naturel de e est égal à un, c’est-à-dire ln(e) = 1.
- Le logarithme naturel de un est égal à zéro, c’est-à-dire ln(1) = 0.
Le tracé de la fonction logarithmique naturelle:
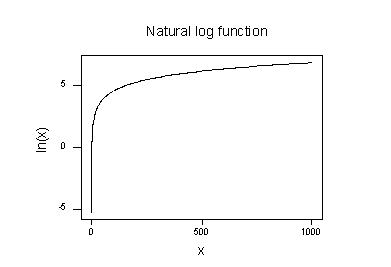
suggère que les effets de la prise de la transformation logarithmique naturelle sont:
- Les petites valeurs proches les unes des autres sont étalées plus loin.
- Les grandes valeurs étalées sont rapprochées.
Retour à l’exemple. Utilisons le logarithme naturel pour transformer les valeurs x dans les données de l’expérience de rétention de mémoire. Puisque x = time est le prédicteur, il suffit de prendre le logarithme naturel de chaque valeur temporelle apparaissant dans l’ensemble de données. Ce faisant, nous créons un prédicteur nouvellement transformé appelé lntime:
| time | prop | lntime |
| 1 | 0.84 | 0.00000 |
| 5 | 0.71 | 1.60944 |
| 15 | 0.61 | 2.70805 |
| 30 | 0.56 | 3.40120 |
| 60 | 0.54 | 4.09434 |
| 120 | 0.47 | 4.78749 |
| 240 | 0.45 | 5.48064 |
| 480 | 0.38 | 6.17379 |
| 720 | 0.36 | 6.57925 |
| 1440 | 0.26 | 7.27240 |
| 2880 | 0.20 | 7.96555 |
| 5760 | 0.16 | 8.65869 |
| 10080 | 0.08 | 9.21831 |
We take the natural logarithm for each value of time and place the results in their own column. C’est-à-dire que nous « transformons » chaque valeur de temps de prédicteur en une valeur ln (time). Par exemple, ln(1) = 0, ln(5) = 1,60944 et ln(15) = 2,70805, etc.
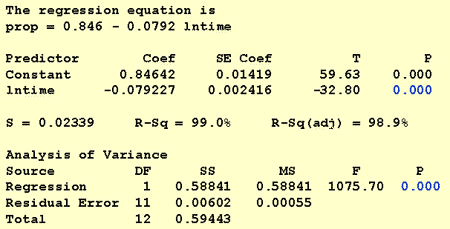
Maintenant que nous avons transformé les valeurs prédictives, voyons si cela a aidé à corriger la tendance non linéaire des données. Nous réajustons le modèle avec y = prop comme réponse et x = lntime comme prédicteur.
Le tracé linéaire ajusté résultant suggère que la prise du logarithme naturel des valeurs prédictives est utile.
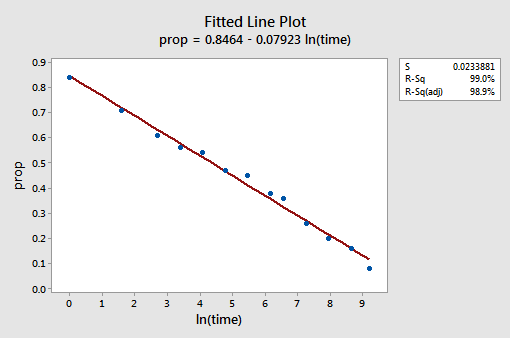
En effet, la valeur R2 est passée de 57,1% à 99,0%. Il nous indique que 99% de la variation de la proportion de mots rappelés (prop) est réduite en tenant compte du journal naturel du temps (lntime)!
Le nouveau graphique résiduel vs.fits montre une amélioration significative par rapport à celui basé sur les données non transformées.
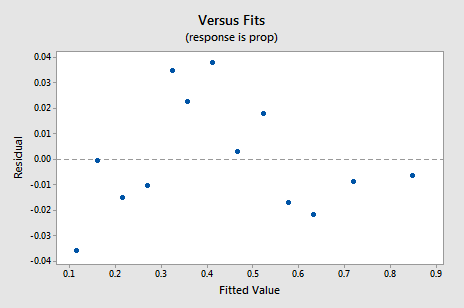
Vous pourriez être préoccupé par une sorte de tendance cyclique ascendante-descendante dans le tracé. Je vous mets encore une fois en garde de ne pas surinterpréter ces tracés, surtout lorsque l’ensemble de données est petit comme celui-ci. Vous ne devriez vraiment pas vous attendre à la perfection lorsque vous avez recours à des transformations de données. Parfois, vous devez simplement vous contenter d’améliorations significatives. À propos, l’intrigue suggère également qu’il est acceptable de supposer que les variances d’erreur sont égales.
Le diagramme de probabilité normal des résidus montre que la transformation des valeurs x n’a eu aucun effet sur la normalité des termes d’erreur:
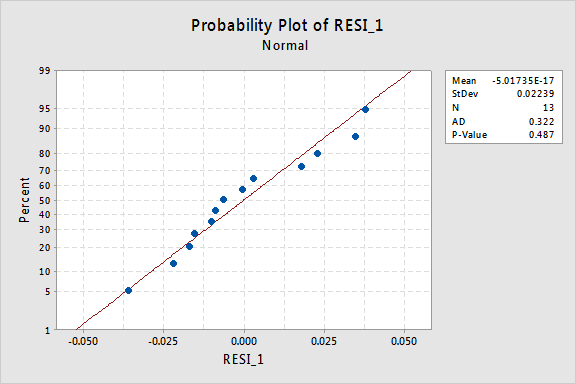
Encore une fois, la valeur P d’Anderson-Darling est grande, nous ne parvenons donc pas à rejeter l’hypothèse nulle des termes d’erreur normaux. Il n’y a pas assez de preuves pour conclure que les termes d’erreurs ne sont pas normaux.
Et si nous avions transformé les valeurs y à la place? Plus tôt, j’ai dit que même si certaines hypothèses peuvent sembler tenir avant d’appliquer une transformation, elles peuvent ne plus tenir une fois qu’une transformation est appliquée. Par exemple, si les termes d’erreur sont bien comportés, la transformation des valeurs y pourrait les transformer en termes d’erreur mal comportés. Les termes d’erreur pour les données de rétention de mémoire avant la transformation des valeurs x semblent être bien comportés (dans le sens où ils apparaissent approximativement normaux). Par conséquent, nous pourrions nous attendre à ce que la transformation des valeurs y au lieu des valeurs x puisse entraîner un mauvais comportement des termes d’erreur. Jetons un coup d’œil aux données de rétention de mémoire pour voir un exemple de ce qui peut arriver lorsque nous transformons les valeurs y lorsque la non-linéarité est le seul problème.
Par essais et erreurs, nous découvrons que la transformation de puissance de y qui fait le meilleur travail pour corriger la non-linéarité est y-1,25. Le tracé linéaire ajusté illustre que la transformation redresse effectivement la relation — bien que ce ne soit pas aussi bien que la transformation logarithmique des valeurs x.
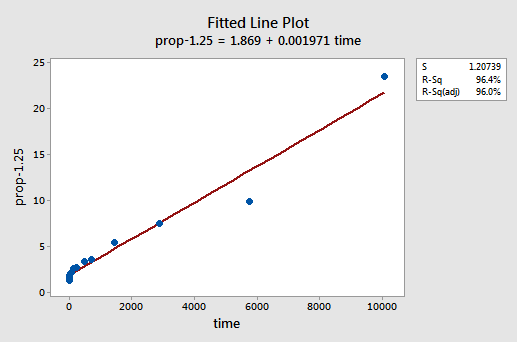
Notez que la valeur R2 est passée de 57,1% à 96,4%.
Les résidus montrent une amélioration par rapport à la non-linéarité, bien que l’amélioration ne soit pas grande…
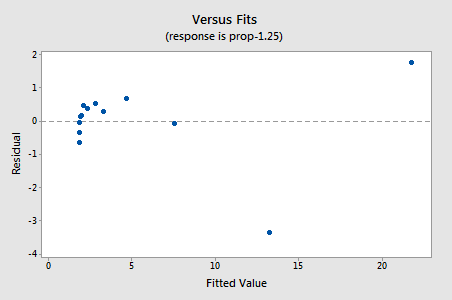
…mais maintenant, nous avons des termes d’erreur non normaux! La valeur P d’Anderson-Darling est inférieure à 0,005, nous rejetons donc l’hypothèse nulle des termes d’erreur normaux. Il existe suffisamment de preuves pour conclure que les termes d’erreur ne sont pas normaux:
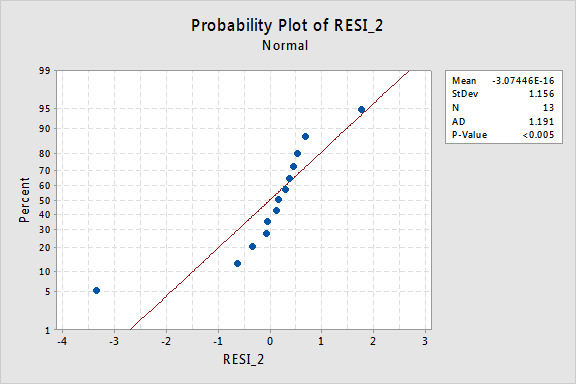
Encore une fois, si les termes d’erreur sont bien comportés avant la transformation, la transformation des valeurs y peut les transformer en termes d’erreur mal comportés.
En utilisant le modèle
Une fois que nous avons trouvé le meilleur modèle pour nos données de régression, nous pouvons ensuite utiliser le modèle pour répondre à nos questions de recherche d’intérêt. Si notre modèle implique des valeurs de prédicteur (x) transformées, il se peut que nous devions ou non apporter de légères modifications aux procédures standard que nous avons déjà apprises.
Utilisons notre modèle de régression linéaire pour les données de rétention de mémoire — avec y=prop comme réponse et x= lntime comme prédicteur — pour répondre à quatre questions de recherche différentes.
Question de recherche #1: Quelle est la nature de l’association entre le temps depuis mémorisé et l’efficacité du rappel?
Pour répondre à cette question de recherche, nous décrivons simplement la nature de la relation. C’est-à-dire que la proportion de mots correctement rappelés est négativement linéairement liée au journal naturel du temps depuis que les mots ont été mémorisés. Sans surprise, à mesure que le journal naturel du temps augmente, la proportion de mots rappelés diminue.
Question de recherche #2:Existe-t-il une association entre le temps écoulé depuis la mémorisation et l’efficacité du rappel?
Pour répondre à cette question de recherche, aucune modification de la procédure standard n’est nécessaire. Nous testons simplement l’hypothèse nulle H0: β1=0 en utilisant soit le test F, soit le test t équivalent :
Comme l’illustre la sortie du logiciel, la valeur P est < 0.001. Il y a des preuves significatives au 0.05 niveau pour conclure qu’il existe une association linéaire entre la proportion de mots rappelés et le log naturel du temps depuis mémorisé.
Question de recherche #3: Quelle proportion de mots pouvons-nous nous attendre à ce qu’une personne sélectionnée au hasard se rappelle après 1000 minutes?
Il suffit de calculer un intervalle de prédiction — avec une légère modification — pour répondre à cette question de recherche. Notre variable prédictive est le journal naturel du temps. Par conséquent, lorsque nous utilisons un logiciel statistique pour calculer l’intervalle de prédiction, nous devons nous assurer de spécifier la valeur des valeurs prédictives dans les unités transformées, et non les unités d’origine. Le log naturel de 1000 minutes est de 6,91 log-minutes. En utilisant un logiciel pour calculer un intervalle de prédiction à 95% lorsque lntime =6,91, nous obtenons :
La sortie nous indique que nous pouvons être sûrs à 95% que, après 1000 jours de minutes, une personne sélectionnée au hasard se souviendra entre 24,5% et 35.3% des mots.
Question de recherche #4:Dans quelle mesure le rappel attendu change-t-il si le temps est multiplié par dix?
Si vous y réfléchissez, répondre à cette question de recherche implique simplement d’estimer et d’interpréter le paramètre de pente β1. Eh bien, pas tout à fait — il y a un léger ajustement. En général, une multiplication par k du prédicteur x est associée à a:
β1 × ln(k)
changement de la moyenne de la réponse y.
Cette dérivation qui suit peut vous aider à comprendre et donc à vous souvenir de cette formule.
Autrement dit, une augmentation dix fois de x est associée à un changement β1 × ln (10) de la moyenne de y. Et une augmentation deux fois de x est associée à un changement β1 × ln (2) de la moyenne de y.
En général, vous ne devez utiliser que des multiples de k qui ont un sens pour la portée du modèle. Par exemple, si les valeurs x de votre ensemble de données vont de 2 à 8, il est logique de considérer k multiples qui sont 4 ou plus petits. Si la valeur de x était 2, une augmentation de dix fois (c’est-à-dire k = 10) vous amènerait de 2 à 2 × 10 = 20, une valeur en dehors de la portée du modèle. Dans l’ensemble de données de rétention de mémoire, les valeurs du prédicteur vont de 1 à 10080, il n’y a donc aucun problème à envisager une augmentation de dix fois.
Si nous ne souhaitons obtenir qu’une estimation ponctuelle, nous prenons simplement l’estimation du paramètre de pente (b1=-0,079227) à partir de la sortie du logiciel :

et la multiplions par ln(10) :
b1 × ln(10) = -0,079227 × ln(10) = -0,182
Nous nous attendons à ce que le pourcentage de mots rappelés diminue (puisque le signe est négatif) 18.2% pour chaque augmentation de dix fois le temps écoulé depuis la mémorisation.
Bien entendu, cette estimation ponctuelle est d’une utilité limitée. Dans quelle mesure pouvons-nous être sûrs que l’estimation est proche de la vraie valeur inconnue? Naturellement, nous devrions calculer un intervalle de confiance de 95%. Pour ce faire, nous calculons simplement un intervalle de confiance de 95% pour β1 comme nous l’avons toujours fait: