i denne delen lærer vi hvordan vi bygger og bruker en enkel lineær regresjonsmodell ved å transformere prediktor x-verdiene. Dette kan være det første du prøver hvis du finner en ikke-lineær trend i dataene dine. Det vil si at transformering av x-verdiene er hensiktsmessig når ikke-linearitet er det eneste problemet (dvs.uavhengigheten, normaliteten og lik variansbetingelsene er oppfylt). Vær imidlertid oppmerksom på at det kan være nødvendig å korrigere ikke-lineariteten før du kan vurdere normalitet og lik variansforutsetninger. Også, mens noen forutsetninger kan synes å holde før du bruker en transformasjon, kan de ikke lenger holde når en transformasjon er brukt. Med andre ord, bruk av transformasjoner er en del av en iterativ prosess der alle lineære regresjonsforutsetninger blir sjekket etter hver iterasjon.Husk at selv om vi fokuserer på en enkel lineær regresjonsmodell her, gjelder de viktige ideene mer generelt for flere lineære regresjonsmodeller også. Vi kan vurdere å transformere noen av prediktorene ved å undersøke scatterplots av residualene versus hver prediktor i sin tur.
Bygg modellen
et eksempel. Den enkleste måten å lære om datatransformasjoner er ved eksempel. La oss vurdere dataene fra et minne oppbevaring eksperiment der 13 fag ble bedt om å huske en liste over frakoblede elementer. Fagene ble deretter bedt om å huske elementene på ulike tider opp til en uke senere. Andelen elementer (y = prop) riktig tilbakekalt på ulike tider (x = tid, i minutter) siden listen ble lagret ble registrert (wordrecall.txt) og plottet. Å erkjenne at det ikke er god grunn til at feilbetingelsene ikke ville være uavhengige, la oss evaluere de resterende tre forholdene — linearitet, normalitet og like avvik — av modellen.
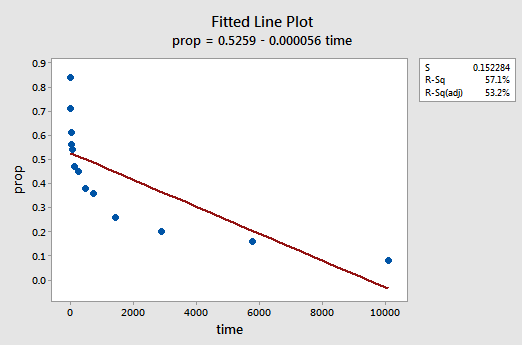
den resulterende monterte linjeplottet antyder at andelen tilbakekalte elementer (y) ikke er lineært relatert til tid (x):
residualene vs. passer plot antyder også at forholdet ikke er lineær:
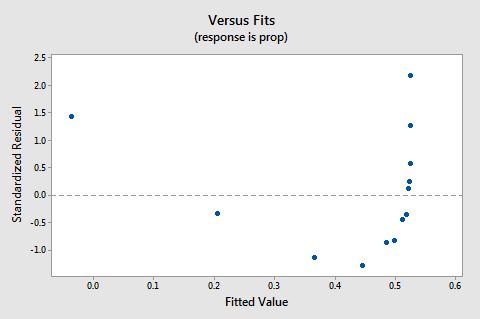
fordi mangelen på linearitet dominerer plottet, kan vi ikke bruke plottet til å vurdere om feilavvikene er like. Vi må løse ikke-linearitetsproblemet før vi kan vurdere antagelsen om like avvik.
hva med den normale sannsynlighetsplottet for residualene? Hva foreslår det om feilbetingelsene? Kan vi konkludere med at de er normalfordelt?
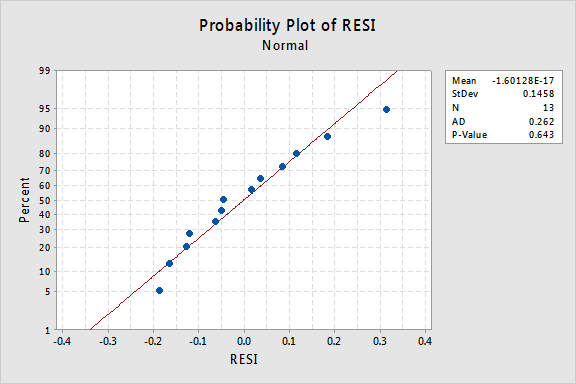
Anderson-Darling p-verdien for dette eksemplet er 0,643, noe som tyder på at vi ikke klarer å avvise nullhypotesen for normale feilvilkår. Det er ikke nok bevis for å konkludere med at feilbetingelsene ikke er normale.i sammendraget har vi et datasett der ikke-linearitet er det eneste store problemet. Denne situasjonen skriker ut for å transformere bare prediktorens verdier. Før vi gjør det, la oss ta en til side og diskutere «logaritmisk transformasjon», siden det er den vanligste og mest nyttige datatransformasjonen tilgjengelig.
den logaritmiske transformasjonen. Standard logaritmisk transformasjon innebærer bare å ta den naturlige logaritmen-betegnet ln eller loge eller bare log — av hver dataverdi. Man kan vurdere å ta en annen type logaritme, for eksempel loggbase 10 eller loggbase 2. Men den naturlige logaritmen – som kan betraktes som loggbase e hvor e er konstanten 2.718282… – er den vanligste logaritmiske skalaen som brukes i vitenskapelig arbeid.
de generelle egenskapene til den naturlige logaritmefunksjonen er:
- den naturlige logaritmen til x er kraften til e = 2,718282… at du må ta for å få x. Dette kan angis notasjonelt som ln (ex) = x.for eksempel er den naturlige logaritmen til 5 den kraften du må heve e = 2,718282… for å få 5. Siden 2.7182821.60944 er omtrent 5, sier vi at den naturlige logaritmen til 5 er 1.60944. Notasjonelt sier vi ln (5) = 1.60944.
- den naturlige logaritmen til e er lik en, det vil si ln (e) = 1.
- den naturlige logaritmen til en er lik null, det vil si ln(1) = 0.
plottet til den naturlige logaritmefunksjonen:
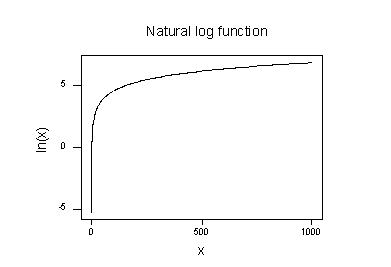
antyder at effekten av å ta den naturlige logaritmiske transformasjonen er:
- små verdier som er tett sammen spres videre ut.
- Store verdier som er spredt ut, bringes nærmere sammen.
Tilbake til eksemplet. La oss bruke den naturlige logaritmen til å transformere x-verdiene i minnelagringseksperimentdataene. Siden x = tid er prediktoren, er alt vi trenger å gjøre, å ta den naturlige logaritmen til hver tidsverdi som vises i datasettet. Ved å gjøre det oppretter vi en nylig transformert prediktor kalt lntime:
| tid | prop | lntime | 1 | 0,84 | 0.00000 |
| 5 | 0.71 | 1.60944 |
| 15 | 0.61 | 2.70805 |
| 30 | 0.56 | 3.40120 |
| 60 | 0.54 | 4.09434 |
| 120 | 0.47 | 4.78749 |
| 240 | 0.45 | 5.48064 |
| 480 | 0.38 | 6.17379 |
| 720 | 0.36 | 6.57925 |
| 1440 | 0.26 | 7.27240 |
| 2880 | 0.20 | 7.96555 |
| 5760 | 0.16 | 8.65869 |
| 10080 | 0.08 | 9.21831 |
We take the natural logarithm for each value of time and place the results in their own column. Det vil si at vi «forvandler» hver prediktor tidsverdi til en ln (tid) verdi. For eksempel, ln(1) = 0, ln(5) = 1,60944, og ln(15) = 2,70805, og så videre.
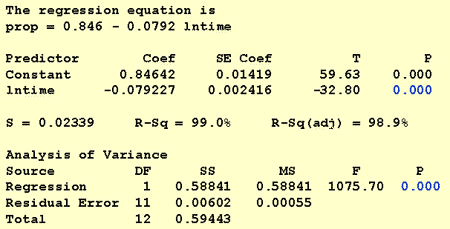
Nå som vi har forvandlet prediktorverdiene, la oss se om det bidro til å korrigere den ikke-lineære trenden i dataene. Vi re-fit modellen med y = prop som svar og x = lntime som prediktor.
den resulterende monterte linjeplottet antyder at det er nyttig å ta den naturlige logaritmen til prediktorverdiene.
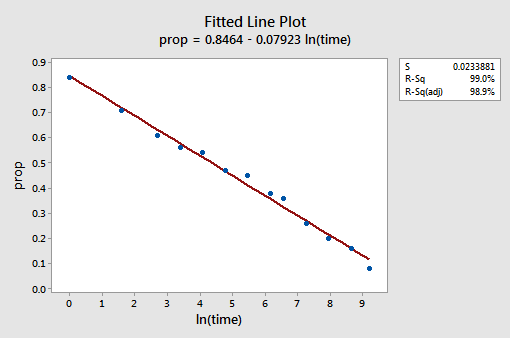
Faktisk har r2-verdien økt fra 57,1% til 99,0%. Det forteller oss at 99% av variasjonen i andelen tilbakekalte ord (prop) reduseres ved å ta hensyn til den naturlige tidsloggen (lntime)!
den nye residual vs. fits-plottet viser en betydelig forbedring i forhold til den som er basert på de ikke-transformerte dataene.
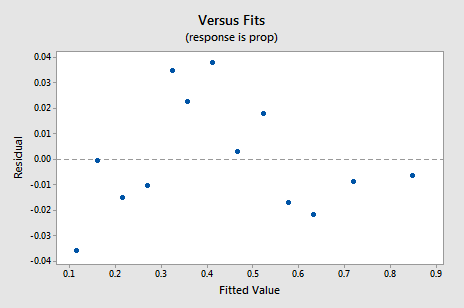
Du kan bli bekymret for en slags opp-ned syklisk trend i plottet. Jeg advarer deg igjen for ikke å overfortolke disse tomtene, spesielt når datasettet er lite som dette. Du bør virkelig ikke forvente perfeksjon når du ty til å ta datatransformasjoner. Noen ganger må du bare være fornøyd med betydelige forbedringer. Forresten foreslår plottet også at det er greit å anta at feilavvikene er like.
den normale sannsynlighetsplottet for residualene viser at transformering av x-verdiene ikke hadde noen effekt på normaliteten til feilbetingelsene:
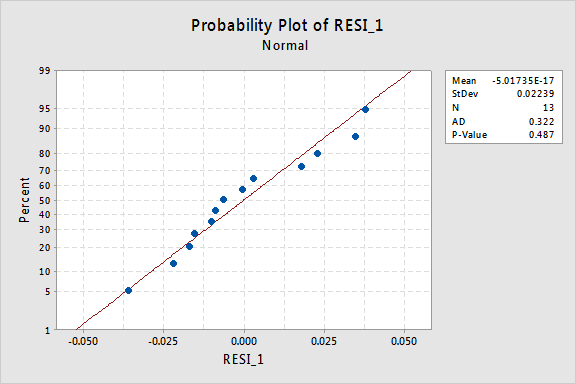
Igjen Er Anderson-Darling p-verdien stor, så vi unnlater å avvise nullhypotesen for normale feilvilkår. Det er ikke nok bevis for å konkludere med at feilbetingelsene ikke er normale.
Hva om vi hadde transformert y-verdiene i stedet? Tidligere sa jeg at mens noen forutsetninger kan synes å holde før du bruker en transformasjon, kan de ikke lenger holde når en transformasjon er brukt. Hvis feilbetingelsene for eksempel er veloppdragen, kan transformering av y-verdiene endre dem til feilaktige feilvilkår. Feilbetingelsene for minnelagringsdataene før transformering av x-verdiene ser ut til å være veloppdragen (i den forstand at de vises omtrent normalt). Derfor kan vi forvente at transformering av y-verdiene i stedet for x-verdiene kan føre til at feilbetingelsene blir dårlig opptatt. La oss ta en rask titt på minnelagringsdataene for å se et eksempel på hva som kan skje når vi forvandler y-verdiene når ikke-linearitet er det eneste problemet.ved prøving og feiling oppdager vi at krafttransformasjonen av y som gjør den beste jobben for å korrigere ikke-lineariteten, er y-1.25. Den monterte linjeplottet illustrerer at transformasjonen faktisk retter ut forholdet-selv om det ikke er så bra som loggtransformasjonen av x-verdiene.
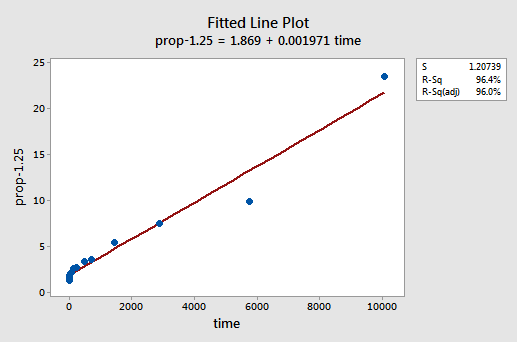
Merk at r2-verdien har økt fra 57,1% til 96,4%.
residualene viser en forbedring med hensyn til ikke-linearitet, selv om forbedringen ikke er stor…
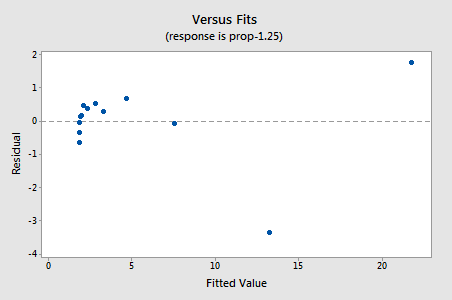
…men nå har vi ikke-normale feilvilkår! Anderson-Darling p-verdien er mindre enn 0,005, så vi avviser nullhypotesen for normale feilvilkår. Det er tilstrekkelig bevis for å konkludere med at feilbegrepene ikke er normale:
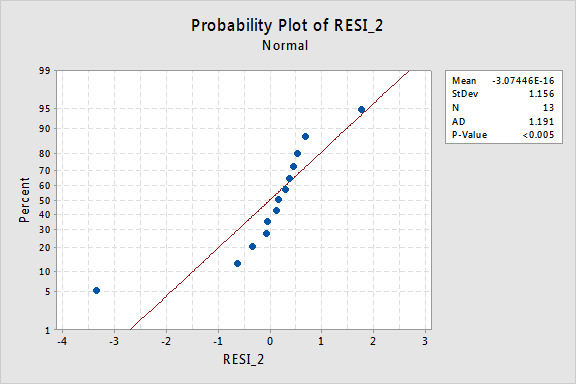
igjen, hvis feilbegrepene er veloppdragen før transformasjon, kan transformering av y-verdiene endre dem til feilbegreper med dårlig oppførsel.
ved hjelp av modellen
Når vi har funnet den beste modellen for våre regresjonsdata, kan vi da bruke modellen til å svare på våre forskningsspørsmål av interesse. Hvis modellen vår innebærer transformerte prediktorverdier( x), kan vi eller ikke måtte gjøre små endringer i standardprosedyrene vi allerede har lært.La oss bruke vår lineære regresjonsmodell for minnelagringsdataene-med y = prop som svar og x = lntime som prediktor-for å svare på fire forskjellige forskningsspørsmål.
Forskningsspørsmål # 1: Hva er arten av sammenhengen mellom tid siden memorisert og effektiviteten av tilbakekalling?
for å svare på dette forskningsspørsmålet beskriver vi bare forholdet. Det vil si at andelen korrekt tilbakekalte ord er negativt lineært relatert til den naturlige loggen av tiden siden ordene ble memorisert. Ikke overraskende, da den naturlige tidsloggen øker, reduseres andelen tilbakekalte ord.
Forskningsspørsmål #2: Er det en sammenheng mellom tid siden memorisert og effektiviteten av tilbakekalling?
ved svar på dette forskningsspørsmålet er det ikke nødvendig å endre standardprosedyren. Vi tester bare nullhypotesen H0: β 1 = 0 ved hjelp Av Enten F-test eller tilsvarende t-test:
Som programvareutgangen illustrerer, er P-verdien < 0.001. Det er betydelige bevis på 0.05 nivå for å konkludere med at det er en lineær sammenheng mellom andelen ord tilbakekalt og den naturlige loggen av tiden siden memorisert.3: hvor stor andel av ord kan vi forvente at en tilfeldig valgt person husker etter 1000 minutter?
Vi trenger bare å beregne et prediksjonsintervall — med en liten modifikasjon — for å svare på dette forskningsspørsmålet. Vår prediktorvariabel er den naturlige tidsloggen. Derfor, når vi bruker statistisk programvare for å beregne prediksjonsintervallet, må vi sørge for at vi angir verdien av prediktorverdiene i de transformerte enhetene, ikke de opprinnelige enhetene. Den naturlige loggen på 1000 minutter er 6,91 log-minutter. Ved hjelp av programvare for å beregne en 95% prediksjon intervall når lntime = 6.91, får vi:
utgangen forteller oss at vi kan være 95% sikre på at, etter 1000 minutter, en tilfeldig valgt person vil huske mellom 24,5% og 35.3% av ordene.
Forskningsspørsmål #4: Hvor mye endres forventet tilbakekalling hvis tiden øker ti ganger?
hvis du tenker på det, innebærer det å svare på dette forskningsspørsmålet bare å estimere og tolke skråningsparameteren β1. Vel, ikke helt—det er en liten justering. Generelt er en k-fold økning i prediktoren x forbundet med a:
β1 × ln (k)
endring i gjennomsnittet av svaret y.
denne avledningen som følger kan hjelpe deg å forstå og derfor huske denne formelen.
Det vil si at en ti ganger økning i x er knyttet til en β1 × ln (10) endring i gjennomsnitt av y. og en dobling i x er knyttet til en β1 hryvnias ln(2) endring i gjennomsnitt av y.
generelt bør du bare bruke multipler av k som gir mening for modellens omfang. Hvis for eksempel x-verdiene i datasettet varierer fra 2 til 8, er det bare fornuftig å vurdere k-multipler som er 4 eller mindre. Hvis verdien av x var 2, vil en ti ganger økning (dvs. k = 10) ta deg fra 2 til 2 × 10 = 20, en verdi utenfor modellens omfang. I minnesretensjonsdatasettet varierer prediktorverdiene fra 1 til 10080, så det er ikke noe problem med å vurdere en ti ganger økning.
Hvis vi bare er interessert i å få et punktestimat, tar vi bare estimatet av skråningsparameteren (b1 = -0.079227) fra programvareutgangen:

og multipliser det med ln(10):
b1 × ln(10) = -0.079227 × ln(10) = -0.182
vi forventer at prosentandelen av tilbakekalte ord vil synke (siden tegnet er negativt) 18.2% for hver ti ganger økning i tiden siden memorisering fant sted.
selvfølgelig er dette punktestimatet av begrenset nytte. Hvor sikre kan vi være at estimatet er nær den sanne ukjente verdien? Naturligvis bør vi beregne et 95% sikkert intervall. For å gjøre det, beregner vi bare et 95% konfidensintervall for β som vi alltid har: