En esta sección, aprendemos a construir y usar un modelo de regresión lineal simple transformando los valores del predictor x. Esto podría ser lo primero que intente si encuentra una tendencia no lineal en sus datos. Es decir, transformar los valores de x es apropiado cuando la no linealidad es el único problema (es decir, se cumplen las condiciones de independencia, normalidad y varianza igual). Tenga en cuenta, sin embargo, que puede ser necesario corregir la no linealidad antes de poder evaluar los supuestos de normalidad y varianza igual. Además, si bien algunas suposiciones pueden parecer válidas antes de aplicar una transformación, es posible que ya no se mantengan una vez que se aplica una transformación. En otras palabras, el uso de transformaciones es parte de un proceso iterativo en el que todas las suposiciones de regresión lineal se vuelven a comprobar después de cada iteración.
Tenga en cuenta que aunque nos estamos centrando en un modelo de regresión lineal simple aquí, las ideas esenciales se aplican de manera más general a los modelos de regresión lineal múltiple también. Podemos considerar transformar cualquiera de los predictores examinando diagramas de dispersión de los residuos versus cada predictor a su vez.
Construyendo el modelo
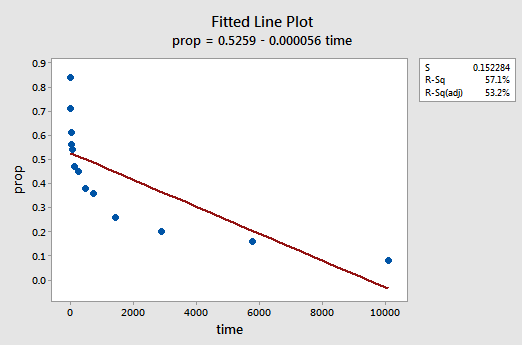
Un ejemplo. La forma más fácil de aprender sobre las transformaciones de datos es a través del ejemplo. Consideremos los datos de un experimento de retención de memoria en el que se pidió a 13 sujetos que memorizaran una lista de elementos desconectados. Luego se les pidió a los sujetos que recordaran los artículos en varias ocasiones hasta una semana después. Se registró la proporción de elementos (y = utilería) que se recordaron correctamente en varias ocasiones (x = tiempo, en minutos) desde que se memorizó la lista (wordrecall.txt)y trazado. Reconociendo que no hay una buena razón para que los términos de error no sean independientes, evaluemos las tres condiciones restantes — linealidad, normalidad y varianzas iguales — del modelo.
La gráfica de línea ajustada resultante sugiere que la proporción de elementos retirados del mercado (y) no está relacionada linealmente con el tiempo (x):
El gráfico de residuos vs. ajustes también sugiere que la relación no es lineal:
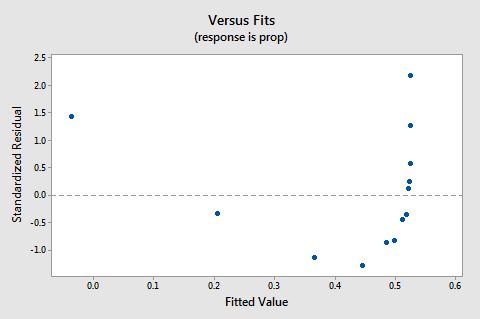
Debido a que la falta de linealidad domina la parcela, no podemos usar la parcela para evaluar si las varianzas de error son iguales o no. Tenemos que solucionar el problema de no linealidad antes de poder evaluar la suposición de varianzas iguales.
¿Qué pasa con la gráfica de probabilidad normal de los residuos? ¿Qué sugiere sobre los términos de error? ¿Podemos concluir que se distribuyen normalmente?
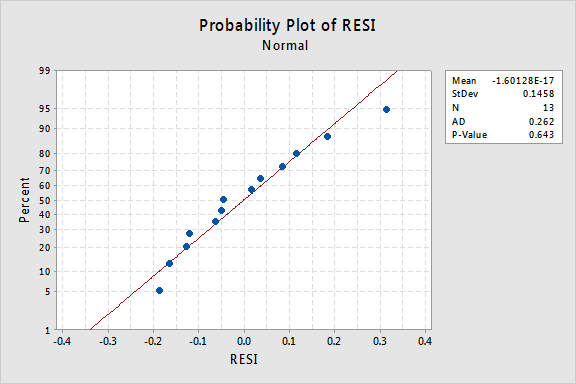
El valor de P de Anderson-Darling para este ejemplo es 0.643, lo que sugiere que no rechazamos la hipótesis nula de los términos de error normales. No hay pruebas suficientes para concluir que los términos de los errores no son normales.
En resumen, tenemos un conjunto de datos en el que la no linealidad es el único problema importante. Esta situación clama por transformar solo los valores del predictor. Antes de hacerlo, hagamos un aparte y discutamos la «transformación logarítmica», ya que es la transformación de datos más común y útil disponible.
La transformación logarítmica. La transformación logarítmica predeterminada simplemente implica tomar el logaritmo natural-denotado ln o loge o simplemente logarítmico-de cada valor de datos. Uno podría considerar tomar un tipo diferente de logaritmo, como el logaritmo base 10 o logaritmo base 2. Sin embargo, el logaritmo natural, que se puede considerar como logaritmo base e, donde e es la constante 2.718282… – es la escala logarítmica más común utilizada en el trabajo científico.
Las características generales de la función logarítmica natural son:
- El logaritmo natural de x es la potencia de e = 2.718282… que tienes que tomar para obtener x. Esto se puede indicar notacionalmente como ln(ex) = x. Por ejemplo, el logaritmo natural de 5 es la potencia a la que tienes que elevar e = 2.718282… para conseguir 5. Dado que 2.7182821.60944 es aproximadamente 5, decimos que el logaritmo natural de 5 es 1.60944. Notacionalmente, decimos ln (5) = 1.60944.
- El logaritmo natural de e es igual a uno, es decir, ln ( e) = 1.
- El logaritmo natural de uno es igual a cero, es decir, ln ( 1) = 0.
La gráfica de la función logaritmo natural:
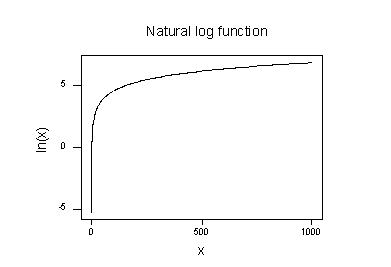
sugiere que los efectos de tomar la transformación logarítmica natural son:
- Los valores pequeños que están muy juntos se extienden más lejos.
- Los valores grandes que se extienden se acercan más.
Volver al ejemplo. Usemos el logaritmo natural para transformar los valores x en los datos del experimento de retención de memoria. Dado que x = time es el predictor, todo lo que necesitamos hacer es tomar el logaritmo natural de cada valor de tiempo que aparece en el conjunto de datos. De esta manera, creamos un nuevo predictor transformado llamado lntime:
| tiempo | prop | lntime |
| 1 | 0.84 | 0.00000 |
| 5 | 0.71 | 1.60944 |
| 15 | 0.61 | 2.70805 |
| 30 | 0.56 | 3.40120 |
| 60 | 0.54 | 4.09434 |
| 120 | 0.47 | 4.78749 |
| 240 | 0.45 | 5.48064 |
| 480 | 0.38 | 6.17379 |
| 720 | 0.36 | 6.57925 |
| 1440 | 0.26 | 7.27240 |
| 2880 | 0.20 | 7.96555 |
| 5760 | 0.16 | 8.65869 |
| 10080 | 0.08 | 9.21831 |
We take the natural logarithm for each value of time and place the results in their own column. Es decir, «transformamos» cada valor de tiempo predictor a un valor ln(tiempo). Por ejemplo, ln(1) = 0, ln(5) = 1.60944, y ln(15) = 2.70805, y así sucesivamente.
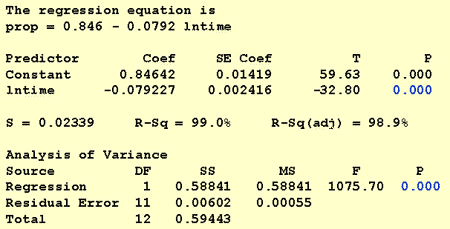
Ahora que hemos transformado los valores predictores, veamos si ayudó a corregir la tendencia no lineal en los datos. Reajustamos el modelo con y = prop como respuesta y x = lntime como predictor.
La gráfica de línea ajustada resultante sugiere que tomar el logaritmo natural de los valores predictores es útil.
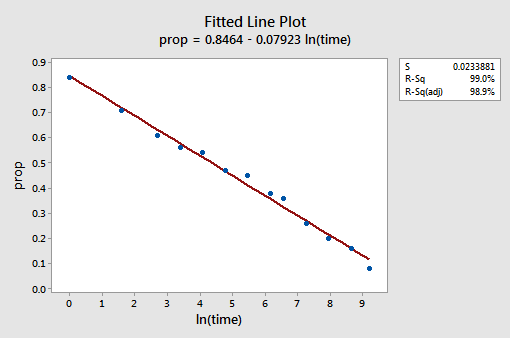
De hecho, el valor R2 ha aumentado del 57,1% al 99,0%. Nos dice que el 99% de la variación en la proporción de palabras recordadas (prop) se reduce teniendo en cuenta el logaritmo natural del tiempo (lntime).
La nueva gráfica residual vs. ajustes muestra una mejora significativa con respecto a la basada en los datos no transformados.
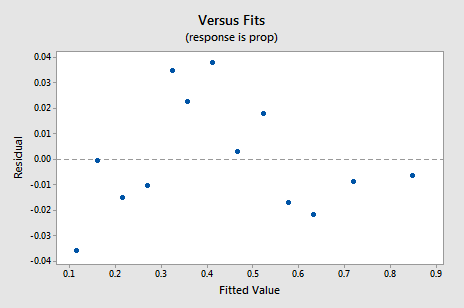
Puede que le preocupe algún tipo de tendencia cíclica ascendente-descendente en la gráfica. Le advierto de nuevo que no sobreinterprete estas gráficas, especialmente cuando el conjunto de datos es pequeño como este. Realmente no debe esperar perfección cuando recurre a realizar transformaciones de datos. A veces tienes que contentarte con mejoras significativas. Por cierto, la gráfica también sugiere que está bien asumir que las variaciones de error son iguales.
La gráfica de probabilidad normal de los residuos muestra que la transformación de los valores de x no tuvo ningún efecto en la normalidad de los términos de error:
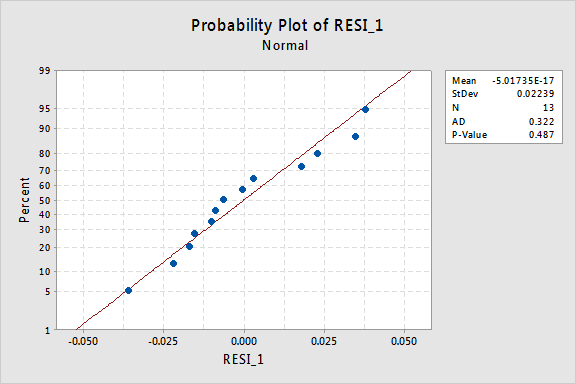
De nuevo, el valor P de Anderson-Darling es grande, por lo que no rechazamos la hipótesis nula de los términos de error normales. No hay pruebas suficientes para concluir que los términos de los errores no son normales.
¿Y si en su lugar hubiéramos transformado los valores de y? Anteriormente dije que, si bien algunas suposiciones pueden parecer válidas antes de aplicar una transformación, es posible que ya no se mantengan una vez que se aplica una transformación. Por ejemplo, si los términos de error se comportan bien, la transformación de los valores y podría cambiarlos en términos de error de mal comportamiento. Los términos de error para los datos de retención de memoria antes de transformar los valores x parecen tener un buen comportamiento (en el sentido de que parecen aproximadamente normales). Por lo tanto, podríamos esperar que la transformación de los valores de y en lugar de los valores de x podría causar que los términos de error se comporten mal. Echemos un vistazo rápido a los datos de retención de memoria para ver un ejemplo de lo que puede suceder cuando transformamos los valores y cuando la no linealidad es el único problema.
Por ensayo y error, descubrimos que la transformación de potencia de y que hace el mejor trabajo para corregir la no linealidad es y-1.25. La gráfica de línea ajustada ilustra que la transformación endereza la relación, aunque es cierto que no tan bien como la transformación logarítmica de los valores x.
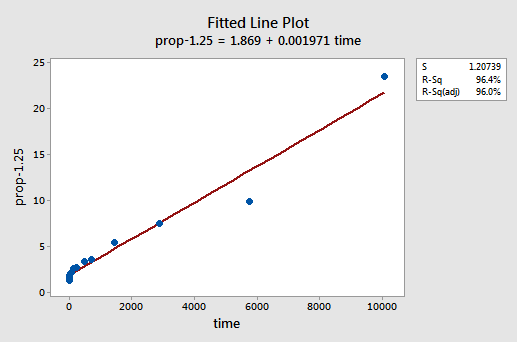
Tenga en cuenta que el valor R2 ha aumentado del 57,1% al 96,4%.
Los residuos muestran una mejora con respecto a la no linealidad, aunque la mejora no es grande…
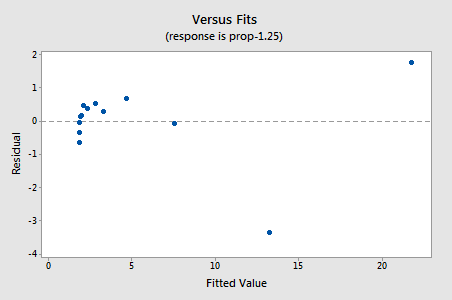
…¡pero ahora tenemos términos de error no normales! El valor de P de Anderson-Darling es inferior a 0,005, por lo que rechazamos la hipótesis nula de los términos de error normales. Hay suficiente evidencia para concluir que los términos de error no son normales:
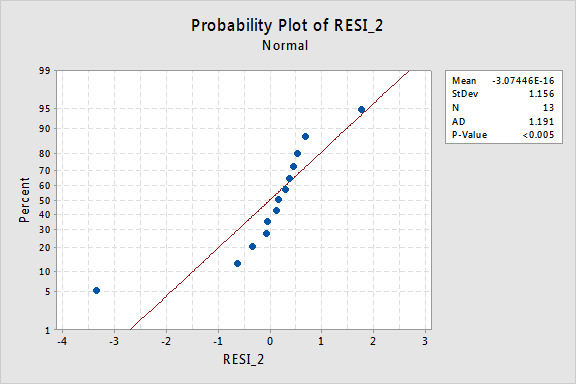
De nuevo, si los términos de error se comportan bien antes de la transformación, la transformación de los valores y puede cambiarlos en términos de error de mal comportamiento.
Usando el modelo
Una vez que hemos encontrado el mejor modelo para nuestros datos de regresión, podemos usar el modelo para responder a nuestras preguntas de investigación de interés. Si nuestro modelo involucra valores predictores transformados (x), es posible que tengamos que hacer o no ligeras modificaciones a los procedimientos estándar que ya hemos aprendido.
Usemos nuestro modelo de regresión lineal para los datos de retención de memoria, con y = prop como respuesta y x = lntime como predictor—para responder a cuatro preguntas de investigación diferentes.
Pregunta de investigación # 1: ¿Cuál es la naturaleza de la asociación entre el tiempo desde que se memorizó y la efectividad del recuerdo?
para responder A esta pregunta de investigación, que acaba de describir la naturaleza de la relación. Es decir, la proporción de palabras recordadas correctamente está relacionada negativamente linealmente con el registro natural del tiempo desde que se memorizaron las palabras. No es sorprendente que, a medida que aumenta el registro natural del tiempo, la proporción de palabras recordadas disminuya.
Pregunta de investigación #2: ¿Existe una asociación entre el tiempo transcurrido desde que se memorizó y la efectividad del recuerdo?
Al responder a esta pregunta de investigación, no es necesario modificar el procedimiento estándar. Simplemente probamos la hipótesis nula H0: β1 = 0 usando la prueba F o la prueba t equivalente:
Como ilustra la salida del software, el valor P es < 0,001. Hay evidencia significativa en el 0.05 nivel para concluir que existe una asociación lineal entre la proporción de palabras recordadas y el logaritmo natural del tiempo transcurrido desde la memorización.
Pregunta de investigación # 3: ¿Qué proporción de palabras podemos esperar que una persona seleccionada al azar recuerde después de 1000 minutos?
Solo necesitamos calcular un intervalo de predicción, con una ligera modificación, para responder a esta pregunta de investigación. Nuestra variable predictora es el logaritmo natural del tiempo. Por lo tanto, cuando usamos software estadístico para calcular el intervalo de predicción, tenemos que asegurarnos de especificar el valor de los valores predictivos en las unidades transformadas, no en las unidades originales. El logaritmo natural de 1000 minutos es de 6,91 logaritmos. Usando software para calcular un intervalo de predicción del 95% cuando lntime = 6.91, obtenemos:
La salida nos dice que podemos estar 95% seguros de que, después de 1000 minutos, una persona seleccionada al azar recordará entre el 24,5% y el 35%.3% de las palabras.
Pregunta de investigación # 4: ¿Cuánto cambia el recuerdo esperado si el tiempo aumenta diez veces?
Si lo piensa, responder a esta pregunta de investigación simplemente implica estimar e interpretar el parámetro de pendiente β1. Bueno, no del todo, hay un ligero ajuste. En general, un aumento de k veces en el predictor x se asocia con un:
β1 × ln(k)
cambio en la media de la respuesta y.
Esta derivación que sigue puede ayudarlo a comprender y, por lo tanto, recordar esta fórmula.
Es decir, un aumento de diez veces en x se asocia con un cambio de β1 × ln(10) en la media de y. Y, un aumento de dos veces en x se asocia con un cambio de β1 × ln(2) en la media de y.
En general, solo debe usar múltiplos de k que tengan sentido para el alcance del modelo. Por ejemplo, si los valores de x en su conjunto de datos van de 2 a 8, solo tiene sentido considerar k múltiplos que sean 4 o menores. Si el valor de x fuera 2, un aumento de diez veces (es decir, k = 10) lo llevaría de 2 a 2 × 10 = 20, un valor fuera del alcance del modelo. En el conjunto de datos de retención de memoria, los valores predictores van de 1 a 10080, por lo que no hay problema en considerar un aumento de diez veces.
Si solo estamos interesados en obtener una estimación puntual, simplemente tomamos la estimación del parámetro de pendiente (b1 = -0.079227) de la salida del software:

y la multiplicamos por ln(10):
b1 × ln(10) = -0.079227 × ln(10) = -0.182
Esperamos que el porcentaje de palabras recordadas disminuya (ya que el signo es negativo) 18.2% por cada diez veces mayor tiempo transcurrido desde que tuvo lugar la memorización.
Por supuesto, esta estimación puntual es de utilidad limitada. ¿Qué tan seguros podemos estar de que la estimación está cerca del verdadero valor desconocido? Naturalmente, debemos calcular un intervalo de confianza del 95%. Para hacerlo, simplemente calculamos un intervalo de confianza del 95% para β1, ya que siempre tenemos: