Netze
Nachfolgend finden Sie eine Reihe von 3D-Formen mit entsprechenden Netzen:
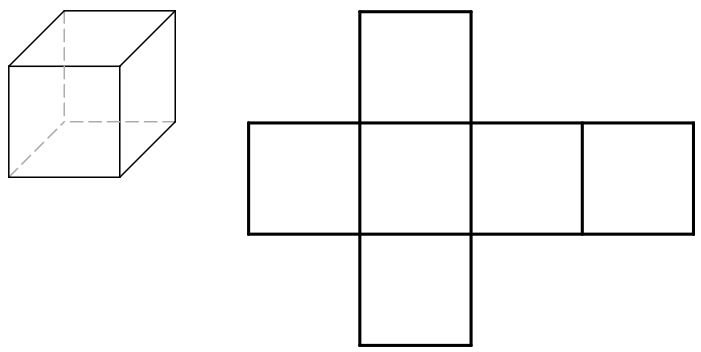
Cubes
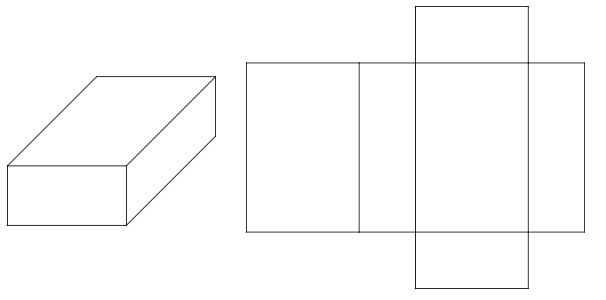
Rectangular Prisms
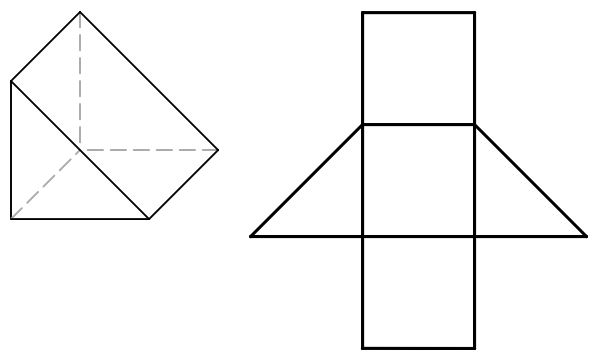
Triangular Prisms
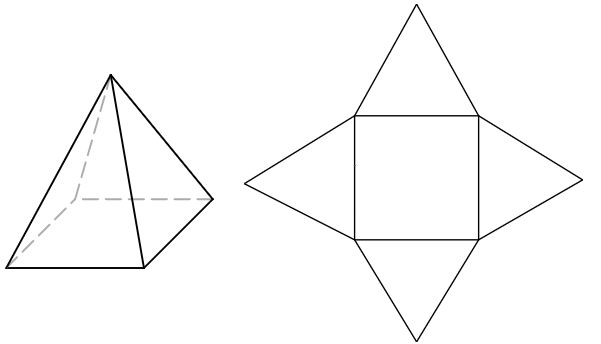
Pyramids
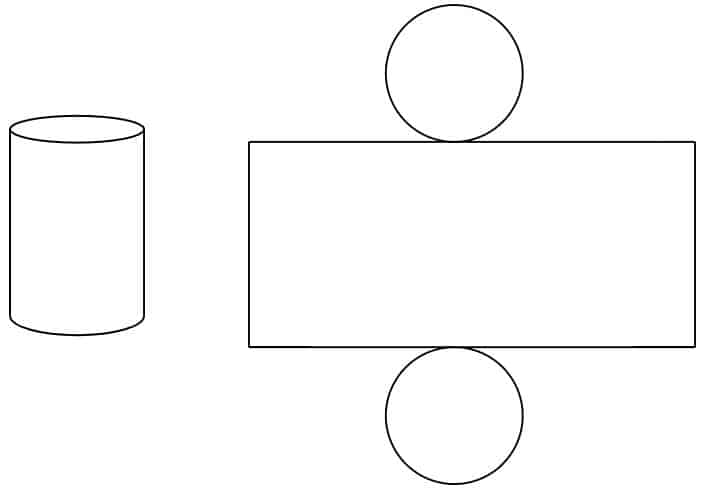
Cylinders
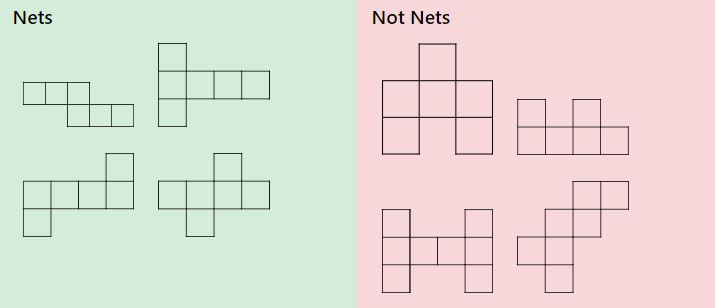
Verschiedene Netze – und Nichtnetze
Netze, die dreidimensionale Formen bilden, können auf unterschiedliche Weise konfiguriert werden. Schauen Sie sich die folgenden Beispiele an und besprechen Sie, welche Netze eines Würfels sind und welche nicht. Mit Hilfe dieses Ausdrucks, der zu einer Vielzahl von 3D-Formen zerschnitten und gefaltet werden kann, können Sie etwas Praktisches üben. Einige Schüler werden am meisten davon profitieren, die vorgezeichneten Netze zu schneiden und zu falten, während andere es genießen werden, zuerst ihre eigenen Netze zu zeichnen, was mit Hilfe dieses druckbaren Millimeterpapiergenerators möglich ist.
Von Netzen zur Oberfläche
Sobald das Konzept der Netze verstanden ist, sollte ihre Verwendung zur Berechnung der Oberfläche einfach werden, obwohl viele Schüler von einer Zusammenfassung der Berechnung der Fläche für 2D-Formen profitieren werden.
Hinweis: Die Schüler verwechseln oft die Begriffe Fläche und Volumen. Seien Sie wachsam und geben Sie einige praktische Beispiele, um zu helfen. Füllen Sie beispielsweise eine Flasche mit Wasser, wickeln Sie sie dann in Papier ein und besprechen Sie in beiden Fällen, wie groß das Volumen und wie groß die Oberfläche ist. Stellen Sie außerdem sicher, dass es keine Sprachbarrieren gibt, die das Verständnis der Schüler beeinträchtigen könnten. z.B. wird der Begriff „Oberfläche“ möglicherweise nicht richtig verstanden.
Fläche mit Netzen: Beispiele
Arbeiten Sie die folgenden Beispiele mit Ihren Kindern durch, bevor Sie mit den Arbeitsblättern für die Fläche üben, die ihnen folgen.
Beispiel – Rechteckiges Prisma #1
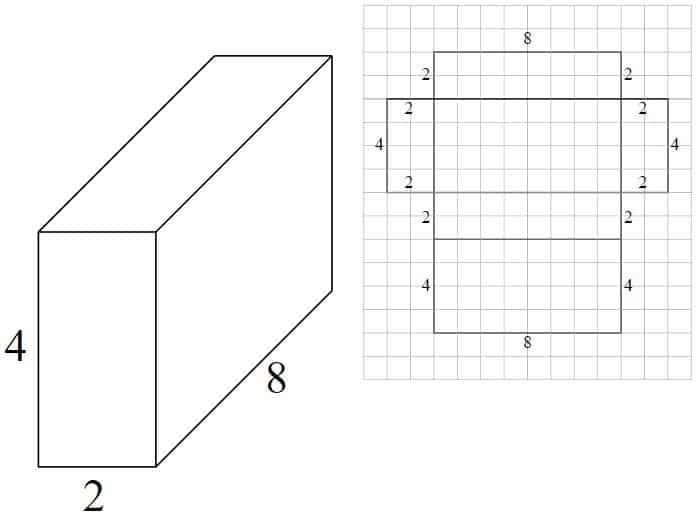
Das Netz besteht aus 6 Rechtecken:
- 8 x 2 = 16
- 8×4 = 32
- 8×2 = 16
- 8×4 = 32
- 2×4 = 8
- 2×4 = 8
- 16 + 32 + 16 + 32 + 8 + 8 = 112 quadratische Einheiten
Besprechen Sie die Berechnung mit Ihren Kindern und heben Sie bei Bedarf hervor, dass die gegenüberliegenden Flächen gleich groß sind und die Berechnung dadurch vereinfacht werden kann. beispielsweise. x 2
Beachten Sie, dass Ihre Kinder möglicherweise nicht sofort alle erforderlichen Abmessungen im Netz erkennen. Helfen Sie ihnen, „fehlende“ Dimensionen aus den angegebenen zu finden.
Beispiel – Rechteckiges Prisma # 2
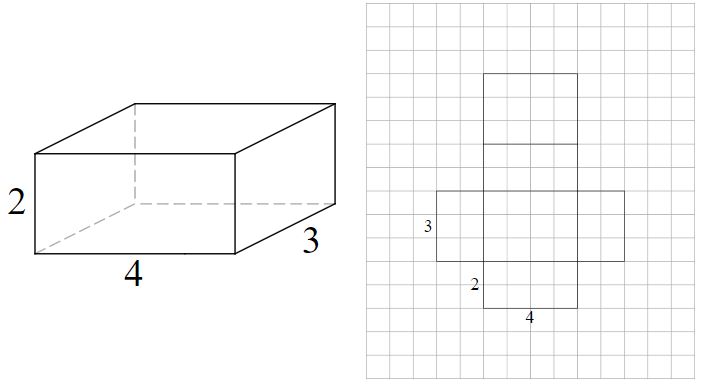
Das Netz besteht aus 6 (2 x 3) Rechtecken. Gegenüberliegende Flächen des Prismas sind gleich.
- (2×4) x 2 = 16
- (4×3) x 2 = 24
- (3×2) x 2 = 12
- 16 + 24 + 12 = 52 quadratische Einheiten
Beispiel – Würfel
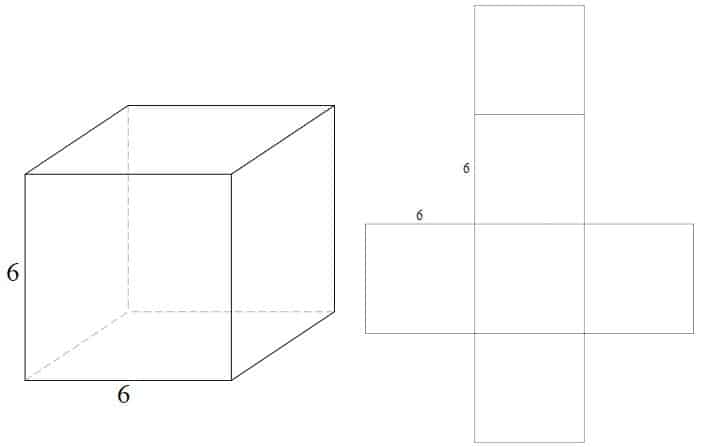
Das Netz eines Würfels besteht aus 6 gleich großen Quadraten
- (4 x 4) x 6 = 96 quadratische Einheiten
Beispiel – Dreiecks-Prisma
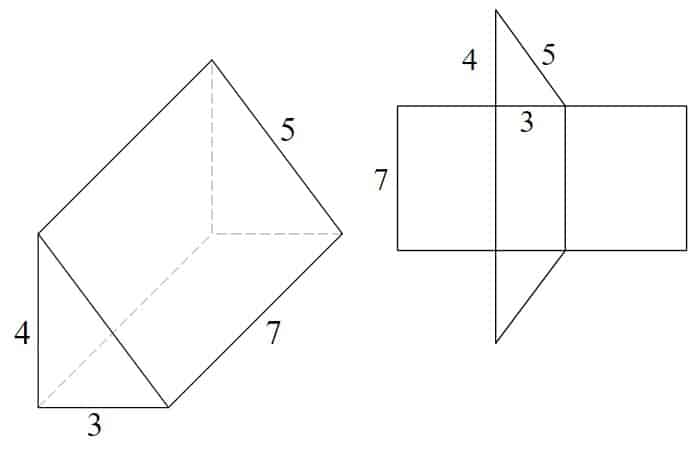
Das Netz aus 3 Rechtecken und 2 gleichgroßen Dreiecken
- 7 x 4 = 28
- 7 x 3 = 21
- 7 x 5 = 35
- (3 x 4 ÷ 2) x 2 = 12
- 28 + 21 + 35 + 12 = 96 quadratische Einheiten
Arbeitsblätter für Netze und Flächen
Die folgenden Arbeitsblätter enthalten eine erste praktische Aktivität mit Anweisungen zum Ausschneiden und Falten, um zu zeigen, wie Netze verschiedene 3D-Formen und ihre Oberflächen darstellen können.
- 3D-Formen und Netze: Ausschneiden und Falten (4-seitiges Arbeitsblatt)
- Formen und Netze zuordnen und zeichnen (2-seitiges Arbeitsblatt)
- Net of not a net? (netze identifizieren)
- Fläche berechnen