hálók
Az alábbiakban számos 3D alakzat található a megfelelő hálókkal:
Cubes
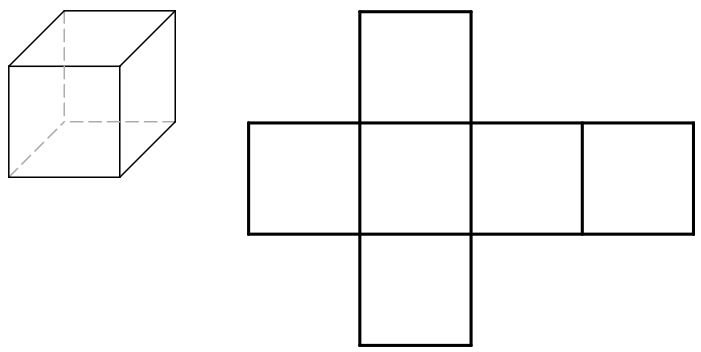
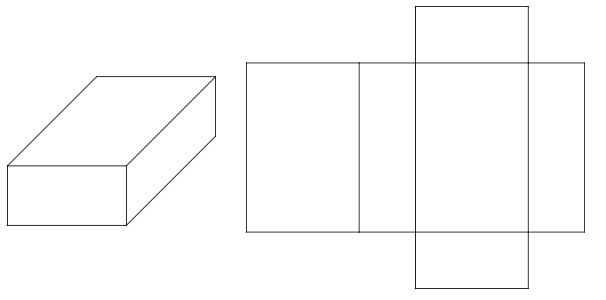
Rectangular Prisms
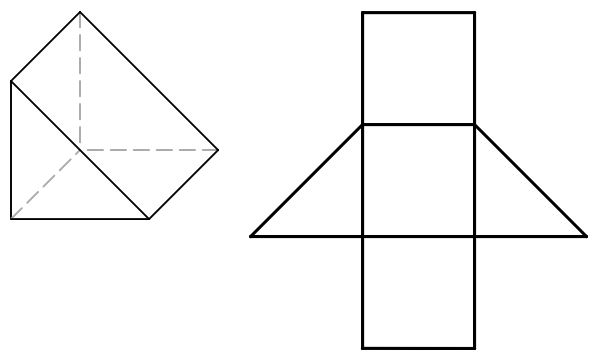
Triangular Prisms
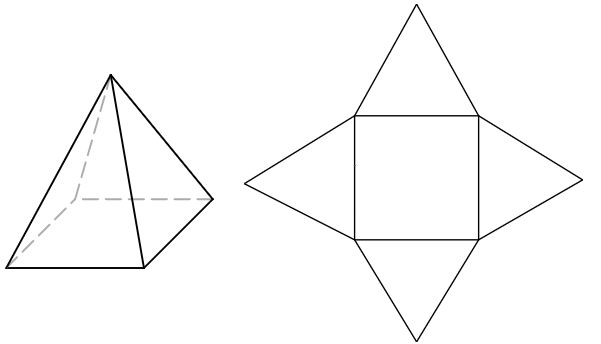
Pyramids
Cylinders
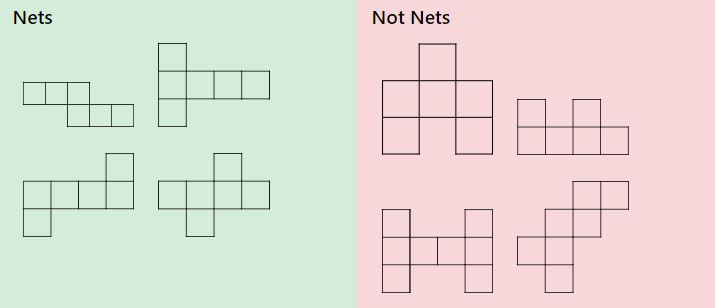
különböző hálók – és nem hálók
A háromdimenziós alakzatokat alkotó hálók különböző módon konfigurálhatók. Nézze meg az alábbi példákat, és beszélje meg, melyek a kocka hálói, és melyek nem. Ennek a nyomtatásnak a segítségével gyakorlati gyakorlatot kaphat, amelyet fel lehet vágni és összehajtani, hogy különféle 3D-s alakzatokat alkosson. Néhány diák kap a legtöbb hasznot vágás és összecsukható az előre húzott hálók, míg mások élvezni rajz saját hálók első, amely lehet tenni a segítségével a nyomtatható grafikon papír generátor.
A hálóktól a felületig
miután a hálók fogalmát megértették, a felület kiszámításához való felhasználásuk egyszerűvé válik, bár sok diák számára előnyös lesz a 2D alakzatok területének kiszámításának összefoglalása.
Megjegyzés: A diákok gyakran összekeverik a terület és a kötet fogalmát. Legyen óvatos erre, és adjon néhány gyakorlati példát, amelyek segítenek. Például töltsön meg egy palackot vízzel, majd tekerje be papírba, és mindkét esetben beszélje meg, mi a térfogat és mi a felület. Győződjön meg arról is, hogy nincsenek olyan nyelvi akadályok, amelyek gátolnák a hallgatók megértését. például előfordulhat, hogy a “felület” kifejezést nem értik megfelelően.
felület hálók használatával: példák
az alábbi példákat dolgozza át gyermekeivel, mielőtt gyakorolna az őket követő felületi munkalapokkal.
példa – négyszögletes prizma #1
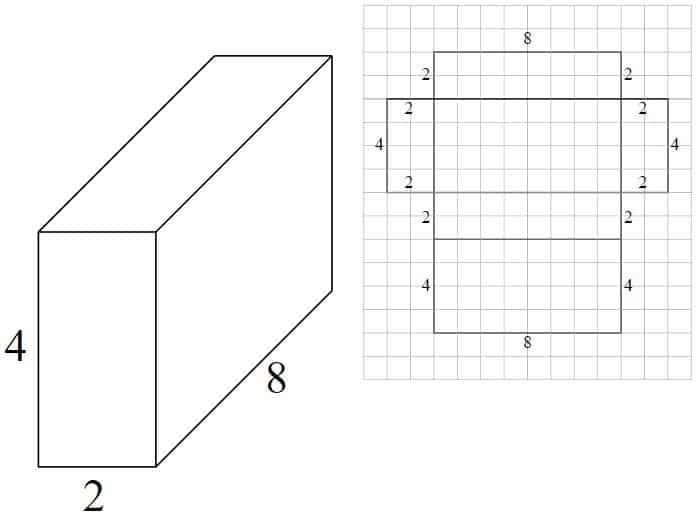
a háló készült 6 téglalapok:
- 8 x 2 = 16
- 8 x 4 = 32
- 8 x 2 = 16
- 8 x 4 = 32
- 2 x 4 = 8
- 2 x 4 = 8
- >16 + 32 + 16 + 32 + 8 + 8 = 112 négyzet egységek
beszélje meg a számítást gyermekeivel, és szükség esetén jelölje ki, hogy az ellenkező arcok dimenziója egyenlő, és ez azt jelenti, hogy a számítás egyszerűsíthető. pl. x 2
ne feledje, hogy gyermekei nem feltétlenül azonosítják azonnal az összes szükséges méretet a neten. Segítsen nekik megtalálni a” hiányzó ” dimenziókat a megadottakból.
példa-téglalap alakú prizma # 2
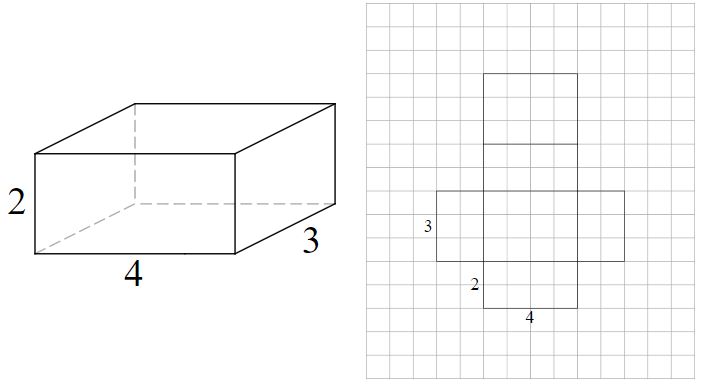
a háló 6 (2 x 3) téglalapból készül. A prizma ellentétes oldalai egyenlőek.
- (2 x 4) x 2 = 16
- (4 x 3) x 2 = 24
- (3 x 2) x 2 = 12
- 16 + 24 + 12 =52 négyzet egység
példa – kocka
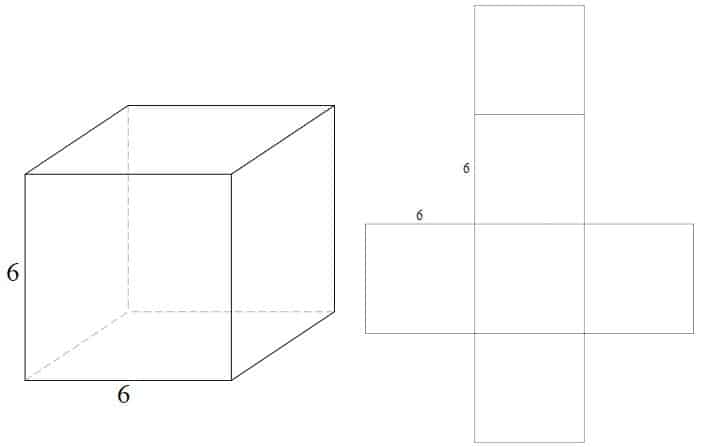
a háló egy kocka készül 6 egyenlő méretű négyzetek
- (4 x 4) x 6=96 négyzet egység
példa-háromszög alakú prizma
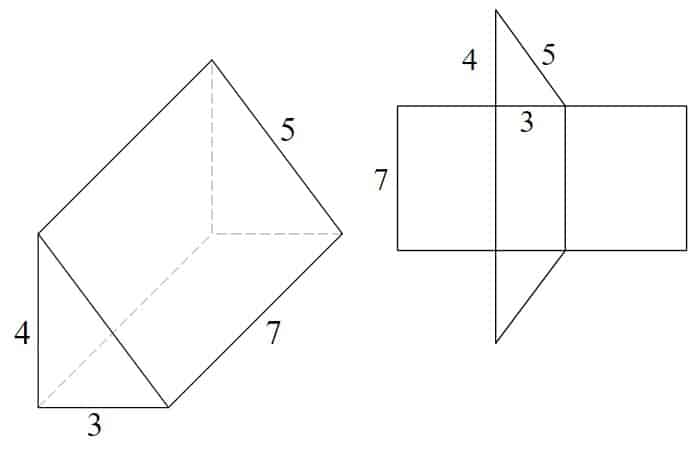
a háló készül 3 téglalapból és 2 egyenlő méretű háromszögből
- 7 x 4 = 28
- 7 x 3 = 21
- 7 x 5 = 35
- (3 x 4 2) x 2 = 12
- 28 + 21 + 35 + 12 = 96 négyzet egységek
hálók és felületi munkalapok
az alábbi munkalapok egy kezdeti gyakorlati tevékenységet tartalmaznak kivágási és hajtogatási utasításokkal, amelyek megmutatják, hogy a hálók hogyan ábrázolhatják a különböző 3D alakzatokat és azok felületét.
- 3D alakzatok és hálók: Kivágás és hajtogatás (4 oldalas tevékenységi munkalap)
- egyezés és rajzolás formák és hálók (2 oldalas munkalap)
- nettó nem háló? (azonosító hálók)
- felület kiszámítása