Garn
Nedenfor er EN rekke 3d-figurer med tilsvarende garn:
Cubes
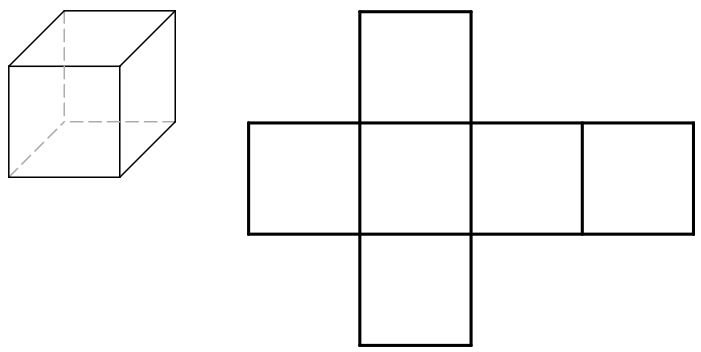
Rectangular Prisms
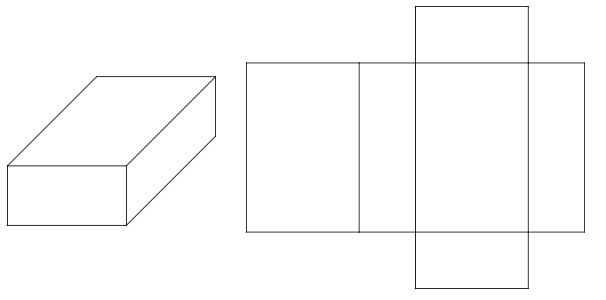
Triangular Prisms
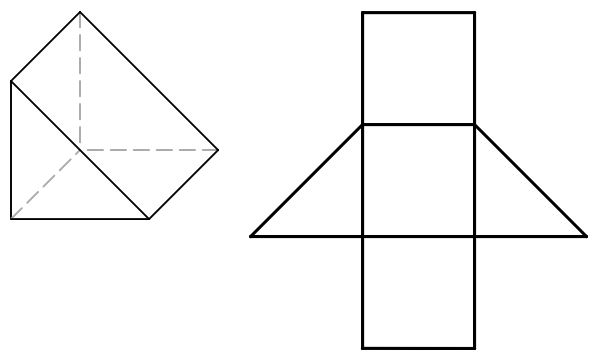
Pyramids
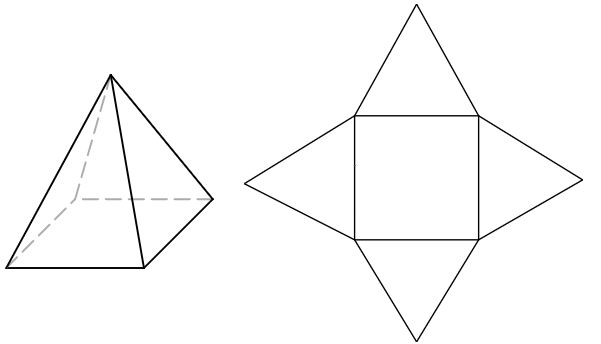
Cylinders
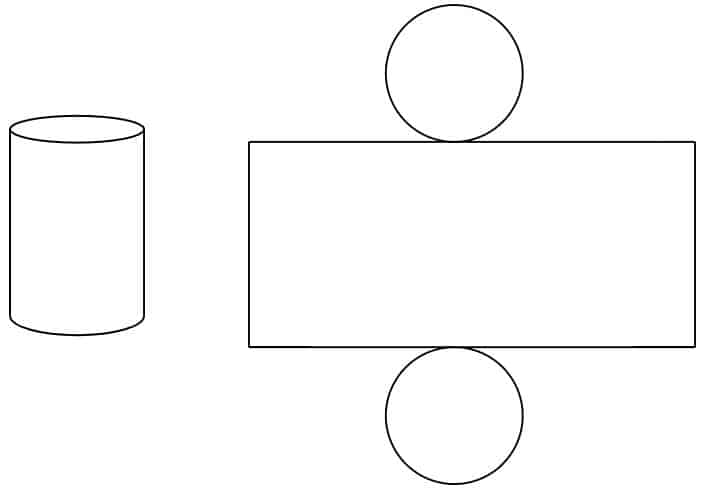
Ulike Nett-og ikke-nett
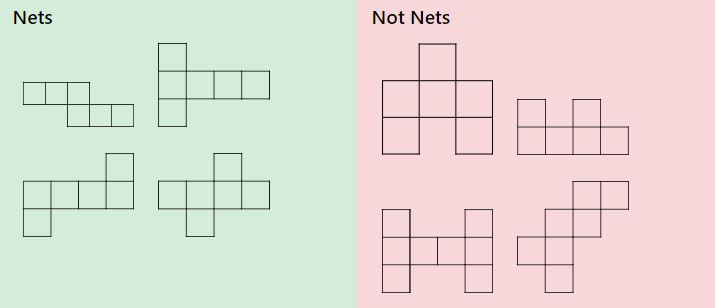
Nett som danner tredimensjonale former kan konfigureres på forskjellige måter. Se og eksemplene nedenfor og diskutere hvilke som er garn av en terning og som ikke er. Du kan få litt praktisk praksis ved hjelp av denne utskriften som kan kuttes opp og brettes for å danne EN rekke 3D-figurer. Noen studenter vil få mest mulig nytte av å kutte og brette de pre-drawn nettene, mens andre vil nyte å tegne sine egne garn først som kan gjøres ved hjelp av denne utskrivbare grafpapirgeneratoren.
fra Garn Til Overflateareal
når begrepet garn er forstått, bør deres bruk for å beregne overflateareal
når begrepet garn er forstått, bør deres bruk for å beregne overflateareal bli grei, selv om mange studenter vil dra nytte av en oppsummering av beregning av areal FOR 2D-figurer.
Merk: Studentene forveksler ofte begreper område og volum. Vær oppmerksom på dette og gi noen praktiske eksempler for å hjelpe. For eksempel, fyll en flaske med vann og pakk den i papir og i begge tilfeller diskutere hva som er volumet og hva er overflaten. Vær også sikker på at det ikke er noen språkbarrierer som kan hemme elevenes forståelse. begrepet «overflate» kan for eksempel ikke forstås riktig.
Overflateareal Ved Hjelp Av Nets: Eksempler
Arbeid gjennom eksemplene nedenfor med barna dine før du trener med overflatearealene som følger dem.
Eksempel – Rektangulært Prisme #1
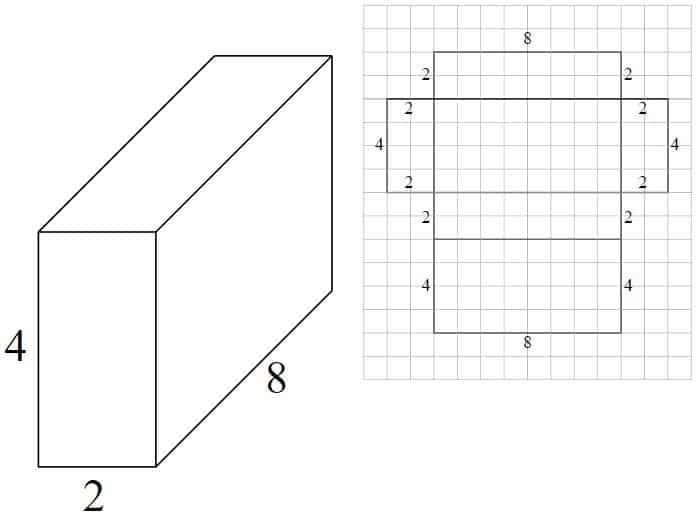
nettet er laget av 6 rektangler:
- 8 x 2 = 16
- 8 X 4 = 32
- 8 x 2 = 16
- 8 x 4 = 32
- 2 x 4 = 8
- 16 + 32 + 16 + 32 + 8 + 8 = 112 kvadratiske enheter
Diskuter beregningen med barna dine og fremhev om nødvendig at motsatte ansikter er like i dimensjon, og at dette betyr at beregningen kan forenkles. eksempelvis. x 2
Vær oppmerksom på at barna ikke umiddelbart kan identifisere alle nødvendige dimensjoner på nettet. Hjelp dem til å finne» manglende » dimensjoner fra de som er gitt.
Eksempel-Rektangulært Prisme #2
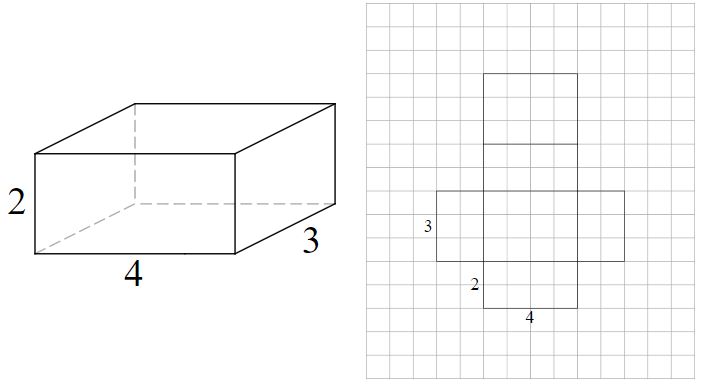
nettet er laget av 6 (2 x 3) rektangler. Motsatte ansikter av prismen er like.
- (2 x 4) x 2 = 16
- (4 x 3) x 2 = 24
- (3 x 2) x 2 = 12
- 16 + 24 + 12 = 52 kvadratiske enheter
Eksempel – Kube
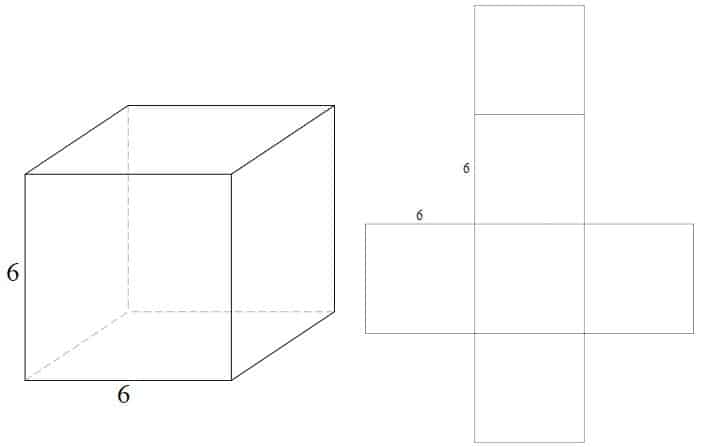
nettet av en kube er laget av 6 like store firkanter
- (4 x 4) x 6 = 96 kvadratiske enheter
eksempel – trekantet prisme
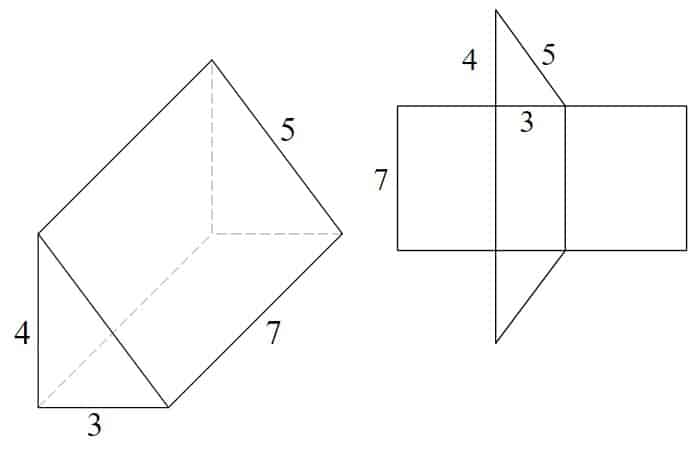
nettet er ikke tilgjengelig. laget fra 3 rektangler og 2 like store trekanter
- 7 x 4 = 28
- 7 x 3 = 21
- 7 x 5 = 35
- (3 x 4 ÷ 2) x 2 = 12
- 28 + 21 + 35 + 12 = 96 square units
Nets And Surface Area Regneark
regnearkene nedenfor inkluderer en innledende hands-on aktivitet med cut-out og fold instruksjoner for å vise hvordan nets kan representert ulike 3D-figurer og deres overflater.
- 3D-Former Og Nett: Cut-out og Fold (4-siders aktivitet regneark)
- Match og tegne figurer og nett (2-siders regneark)
- Netto av ikke et nett? (identifiserende garn)
- Beregning Av Overflateareal