plase
mai jos sunt un număr de forme 3D cu plase corespunzătoare:
Cubes
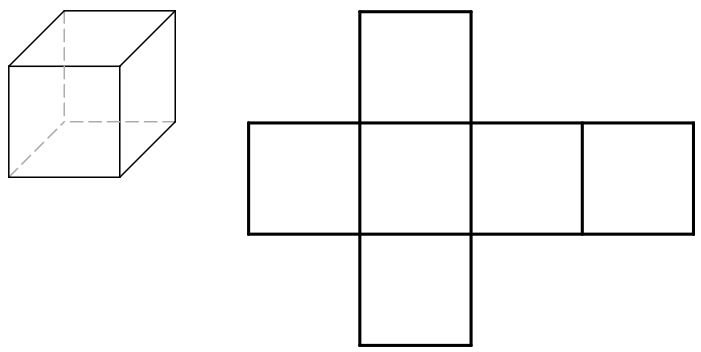
Rectangular Prisms
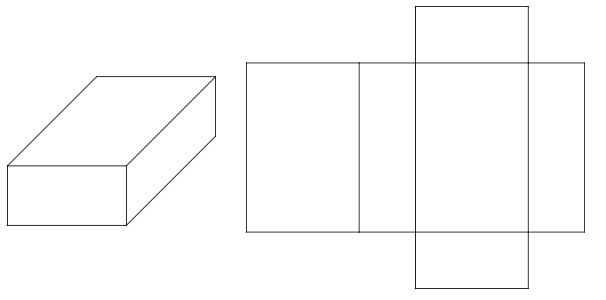
Triangular Prisms
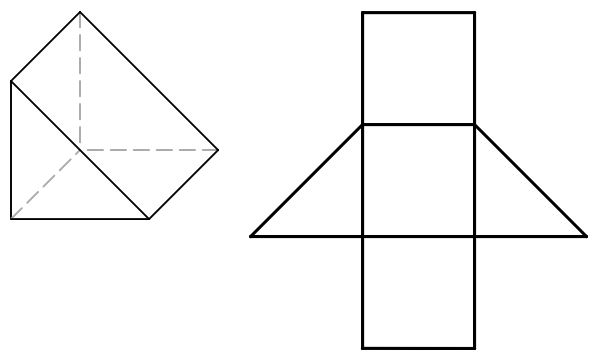
Pyramids
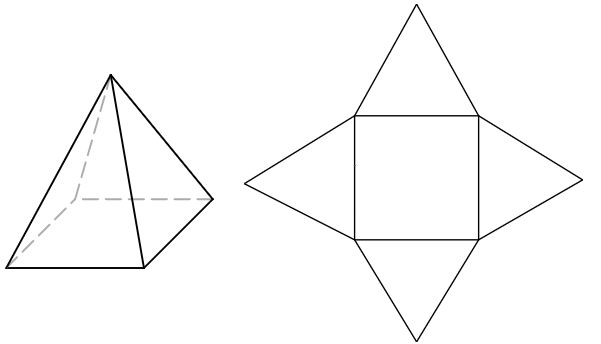
Cylinders
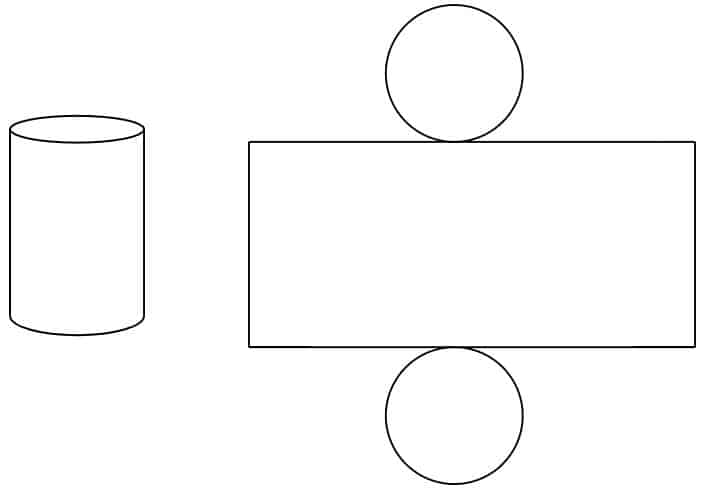
diferite plase – și non-plase
plasele care formează forme tridimensionale pot fi configurate în moduri diferite. Uită-te și exemplele de mai jos și discută care sunt plasele unui cub și care nu sunt. Puteți obține unele practici practice cu ajutorul acestui print-out care poate fi tăiat și pliat pentru a forma o varietate de forme 3D. Unii studenți vor beneficia cel mai mult de tăierea și plierea plaselor pre-desenate, în timp ce alții se vor bucura mai întâi de desenarea propriilor plase, ceea ce se poate face cu ajutorul acestui generator de hârtie grafică imprimabilă.
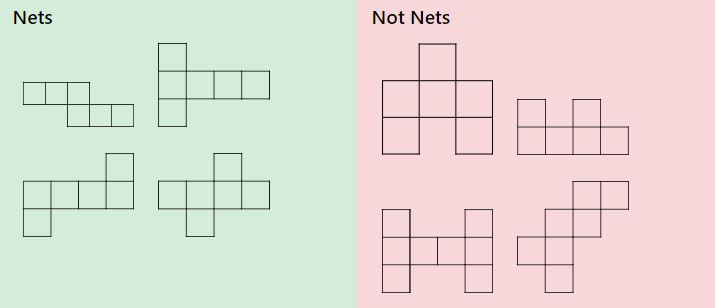
de la plase la suprafață
odată înțeles conceptul de plase, utilizarea lor pentru a ajuta la calcularea suprafeței ar trebui să devină simplă, deși mulți studenți vor beneficia de o recapitulare a suprafeței de calcul pentru formele 2D.
notă: elevii confundă adesea conceptele de zonă și volum. Fiți atenți la acest lucru și oferiți câteva exemple practice pentru a vă ajuta. De exemplu, umpleți o sticlă cu apă, apoi înfășurați-o în hârtie și, în ambele cazuri, discutați care este volumul și care este suprafața. De asemenea, asigurați-vă că nu există bariere lingvistice care ar putea inhiba înțelegerea elevilor. de exemplu, termenul „suprafață” ar putea să nu fie înțeles corect.
suprafață folosind plase: Exemple
parcurgeți exemplele de mai jos împreună cu copiii înainte de a exersa cu foile de lucru pentru suprafață care le urmează.
exemplu – prismă dreptunghiulară #1
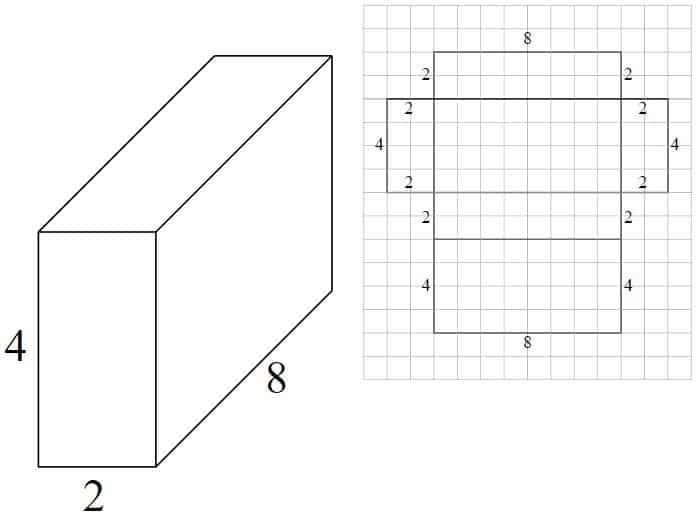
plasa este realizată din 6 dreptunghiuri:
- 8 x 2 = 16
- 8 x 4 = 32
- 8 x 2 = 16
- 8 x 4 = 32
- 2 x 4 = 8
- 2 x 4 = 8
- 16 + 32 + 16 + 32 + 8 + 8 = 112 unități pătrate
discutați calculul cu copiii dvs. și evidențiați, dacă este necesar, că fețele opuse au dimensiuni egale și că acest lucru înseamnă că calculul poate fi simplificat. de ex. x 2
rețineți că este posibil ca copiii dvs. să nu identifice imediat toate dimensiunile necesare pe net. Ajutați-i să găsească dimensiuni „lipsă” din cele date.
exemplu – prismă dreptunghiulară #2
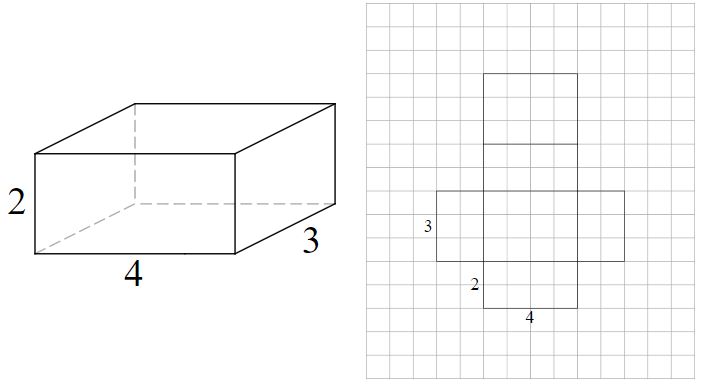
plasa este realizată din 6 (2 x 3) dreptunghiuri. Fețele opuse ale prismei sunt egale.
- (2 x 4) x 2 = 16
- (4 x 3) x 2 = 24
- (3 x 2) x 2 = 12
- 16 + 24 + 12 =52 unități pătrate
exemplu – cub
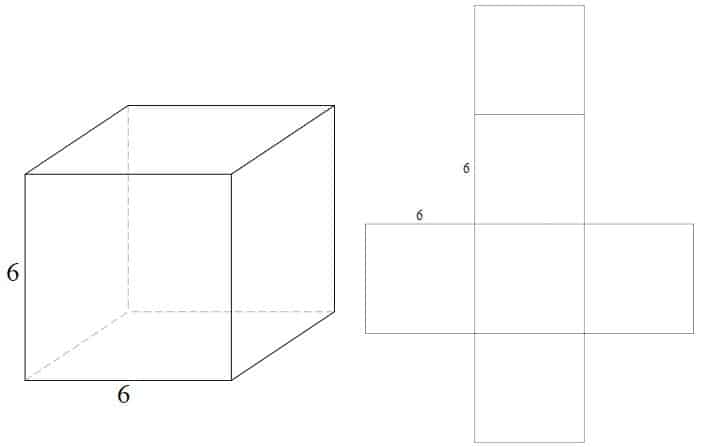
plasa unui cub este realizată din 6 pătrate de dimensiuni egale
- (4 x 4) x 6=96 unități pătrate
exemplu-prisma triunghiulară
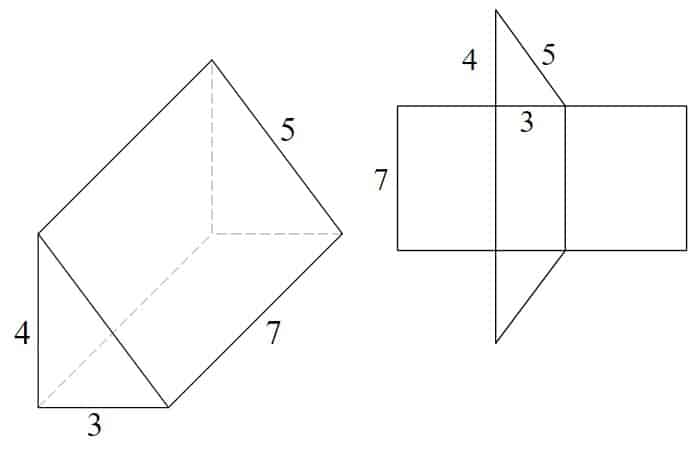
plasa este realizată din de la 3 dreptunghiuri și 2 triunghiuri de dimensiuni egale
- 7 x 4 = 28
- 7 x 3 = 21
- 7 x 5 = 35
- (3 x 4 x 2) x 2 = 12
- 28 + 21 + 35 + 12 = 96 unități pătrate
plase și foi de lucru de suprafață
foile de lucru de mai jos includ o activitate inițială practică cu instrucțiuni de decupare și pliere pentru a arăta cum plasele pot reprezenta diferite forme 3D și suprafețele lor.
- forme și plase 3D: decupați și pliați (foaia de lucru cu activitate de 4 pagini)
- potriviți și desenați forme și plase (foaia de lucru de 2 pagini)
- Net de nu o plasă? (plase de identificare)
- calcularea suprafeței