nät
nedan finns ett antal 3D-former med motsvarande nät:
Cubes
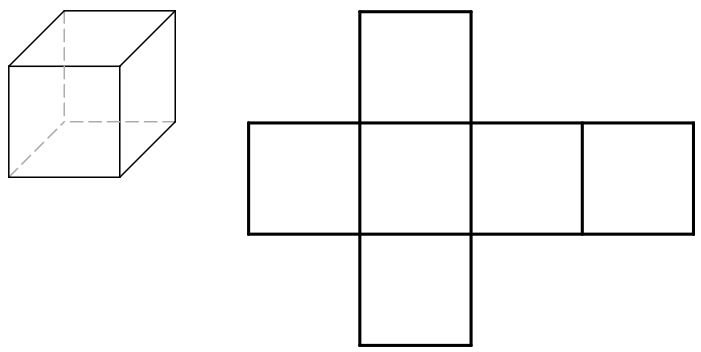
Rectangular Prisms
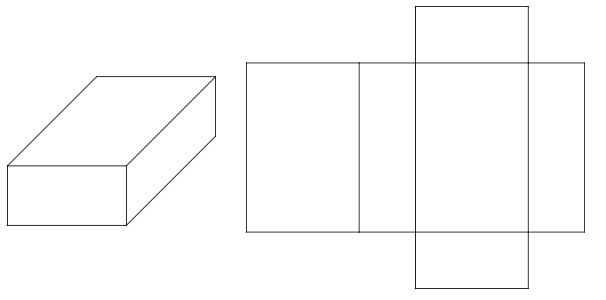
Triangular Prisms
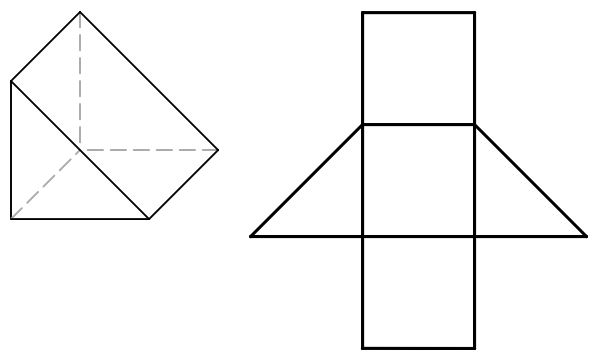
Pyramids
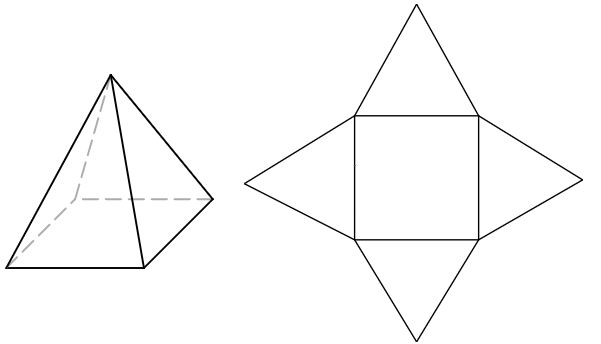
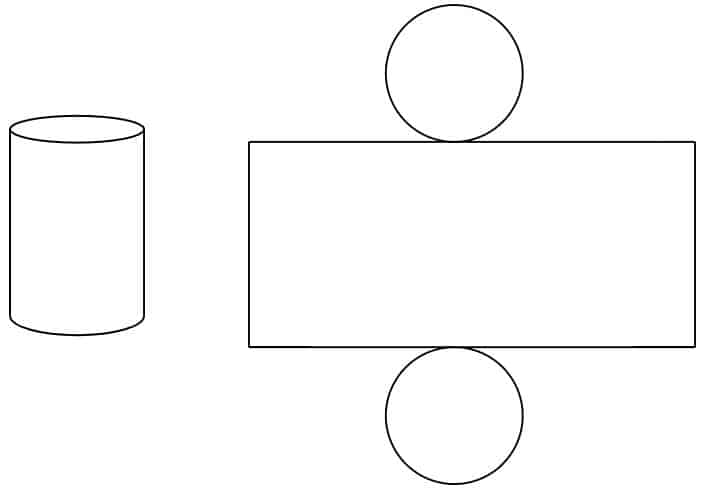
Cylinders
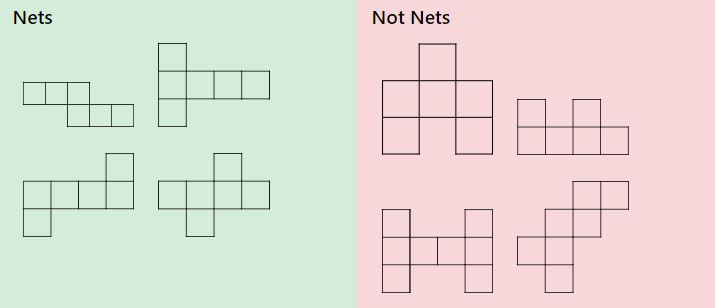
olika nät-och icke-nät
nät som bildar tredimensionella former kan konfigureras på olika sätt. Titta och exemplen nedan och diskutera vilka är nät av en kub och vilka inte. Du kan få lite praktisk övning med hjälp av denna utskrift som kan klippas upp och vikas för att bilda en mängd olika 3D-former. Vissa studenter kommer att få mest nytta av att klippa och vika de fördragna nät medan andra kommer att njuta av att dra sina egna nät först som kan göras med hjälp av denna utskrivbara grafpappersgenerator.
från nät till ytarea
när begreppet nät har förstått bör deras användning för att beräkna ytarean bli enkel även om många studenter kommer att dra nytta av en sammanfattning av beräkningsområdet för 2D-former.
Obs: studenter förvirrar ofta begreppen område och volym. Var uppmärksam på detta och ge några praktiska exempel för att hjälpa. Fyll till exempel en flaska med vatten och linda den sedan i papper och diskutera i båda fallen vad som är volymen och vad som är ytan. Se också till att det inte finns några språkbarriärer som kan hämma elevernas förståelse. t.ex. termen ”yta” kanske inte förstås korrekt.
ytarea med hjälp av nät: exempel
arbeta igenom exemplen nedan med dina barn innan du övar med de arbetsblad för ytarea som följer dem.
exempel – rektangulärt prisma #1
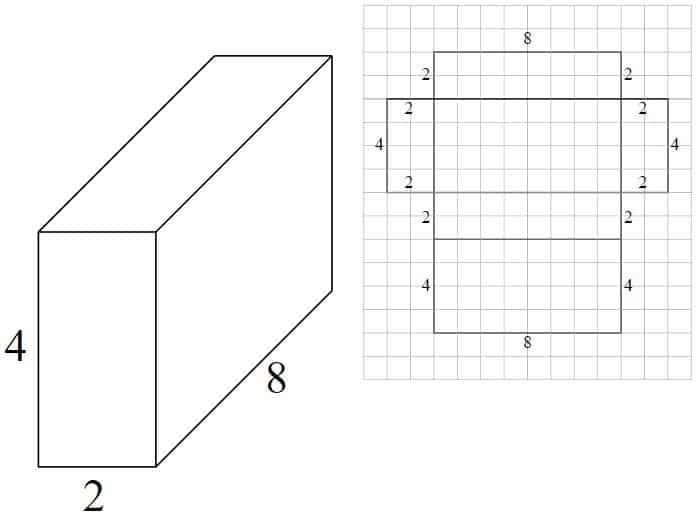
nätet är tillverkat av 6 rektanglar:
- 8 x 2 = 16
- 8 x 4 = 32
- 8 x 2 = 16
- 8 x 4 = 32
- 2 x 4 = 8
- 2 x 4 = 8
- 16 + 32 + 16 + 32 + 8 + 8 = 112 kvadratiska enheter
diskutera beräkningen med dina barn och markera vid behov att motsatta ansikten är lika i dimension och att detta innebär att beräkningen kan förenklas. ex. x 2
tänk på att dina barn kanske inte omedelbart identifierar alla nödvändiga dimensioner på nätet. Hjälp dem att hitta” saknade ” dimensioner från de som ges.
exempel-rektangulärt prisma # 2
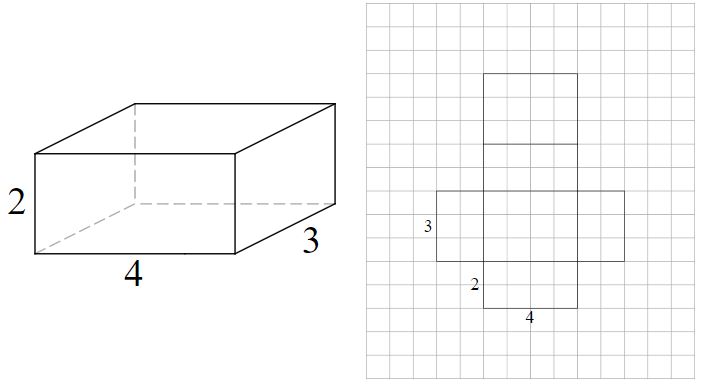
nätet är tillverkat av 6 (2 x 3) rektanglar. Motsatta sidor av prismen är lika.
- (2 x 4) x 2 = 16
- (4 x 3) x 2 = 24
- (3 x 2) x 2 = 12
- 16 + 24 + 12 = 52 kvadratenheter
exempel – kub
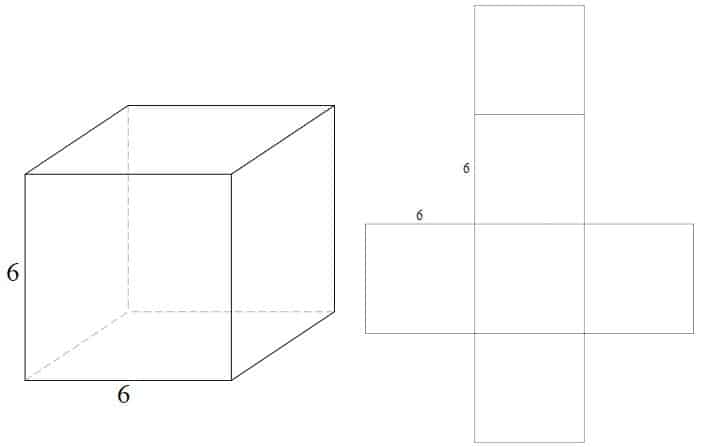
kubens nät är tillverkat av 6 lika stora rutor
- (4 x 4) x 6 = 96 kvadratenheter
exempel – triangulärt prisma
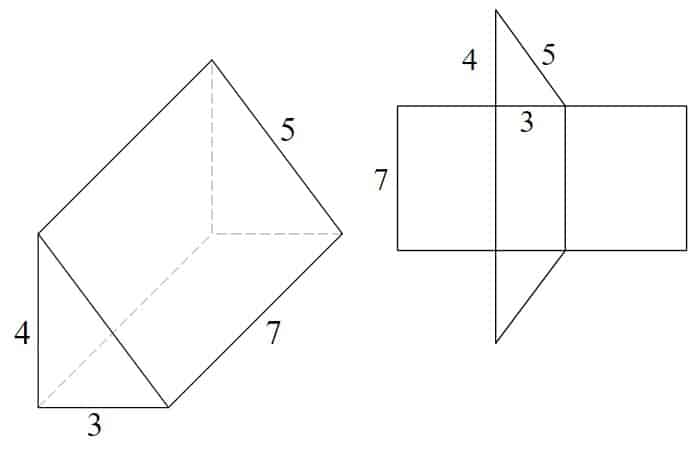
nätet är gjort från 3 rektanglar och 2 lika stora trianglar
- 7 x 4 = 28
- 7 x 3 = 21
- 7 x 5 = 35
- (3 x 4 2 oc) x 2 = 12
- 28 + 21 + 35 + 12 = 96 fyrkantiga enheter
Nät och arbetsblad för ytarea
arbetsbladen nedan innehåller en första praktisk aktivitet med utskurna och vikinstruktioner för att visa hur nät kan representera olika 3D-former och deras ytor.
- 3D-former och nät: Cut-out och Fold (4-sidigt aktivitetsark)
- matcha och rita former och nät (2-sidigt kalkylblad)
- netto av inte ett nät? (identifierande nät)
- beräkning av ytarea